
ll the attention is on the long waited one-month spectacle called the football world cup. The teams are have already arrived in Russia (the host country of FIFA World Cup 2018), the host venues are ready and everyone is waiting for the spectacular tournament. In the meanwhile, bookmakers, football experts, ex-football players and everyone else is trying to predict who will win the precious cup this time. We have seen in the past, the hype around the world cup has brought many interesting and innovative ways to predict the results and the winner including “Paul the Octopus” — the famous octopus which was purportedly used to predict the results of association football matches. His accurate predictions in the 2010 World Cup brought him worldwide attention and labeled him as an animal oracle.
On the other hand, scientists have been trying to place their predictions based on data and scientific methods. Recently, researchers from Technische Universitat Dortmund and Ghent University have released their random forest approach for predicting the outcomes of the World Cup. They compare three different models: Poisson regression models, random forests and ranking methods and they end up with a random forest approach yielding improved predictive power.
Data
The whole approach relies on data from the past World Cup tournaments from 2002 to 2014. The researchers constructed a dataset containing data about the teams and the scores of the previous 4 world cups. The dataset contains variables describing the teams divided into 5 groups: Economic Factors, Sportive Factors, Home Advantage, Team Structure and Team Coach factors. The idea is to use the 16 variables to model the upcoming games and predict the score, which represents the response variable. In fact, they use the number of scored goals as the response variable and restructure the dataset in that way (number of scored goals when team A plays against team B under these circumstances — the other variables representing the other factors). The table below gives the data structured in this way.
Factors
The key to successful modeling and predictive power is the right choice of predictive variables i.e. factors which potentially affect the outcomes of the games (although we all know that the football game is difficult to predict). As mentioned before the authors divide the factors that they identified and collected data about in 5 groups.
Economic Factors
- GDP per capita (Gross domestic product at the time of the World Cup)
- Population (The population size of the country)
Sportive Factors
- ODDSET probability (Bookmaker odds from the German state betting agency)
- FIFA Rank (The rank of the country according to the FIFA Ranking System)
Home Advantage
- Host (Whether the country is a host country or not)
- Continent (Encoding if the country is from the same continent as the host country)
- Confederation (The confederation where it belongs)
Team Structure
- Maximum number of teammates (Maximum number of teammates playing together in a club)
- Average Age (The average age of the players)
- Number of Champions League/Europa League players
- Number of players abroad
Team’s Coach
- Age
- Tenure (Duration of the tenure)
- Nationality
Random Forest
In their work, the researchers use random forest using the previously defined 16 variables as predictors and the number of goals as response variable. In order to prevent overfitting the training data, they construct the trees in the random forest to be pruned and each leaf node to correspond to a distribution of the response variable — number of goals in the form of a simple boxplot.
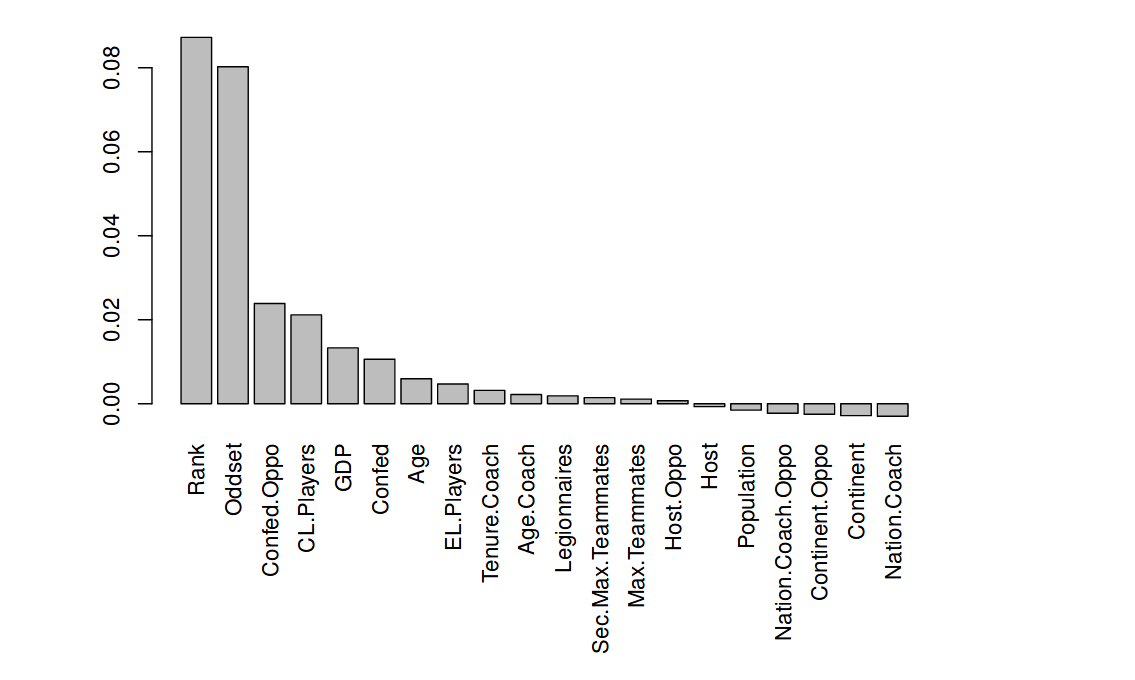
Before running an algorithm to construct the random forest in a usual way, they do variable importance analysis to identify the contribution of each variable to the prediction or the actual outcome. To obtain a variable importance plot, they apply a permutation-based approach to the trees in the random forest. By doing this, they end up with discovering that Rank, Oddset, and CL players are the most important variables carrying the most predictive power. The bar plot shows the ranking of the variables.
Regression
Similarly to the random forest approach, the authors use Lasso regression to predict the outcomes, while at the same time enforcing variable selection. They define the distance metric or difference between the values of the predictor variables and they try to predict to scores per match: the number of scored goals for each team.
Ranking Methods
Moreover, the researchers explore the Poisson model to get rankings of the teams that reflect a team’s current ability. Here, they use the FIFA ranking to derive match importance while giving more importance to recent matches.
Predictions
In the end, they combine all three previously mentioned methods by using a general procedure:
- Form a training dataset containing three out of four World Cups.
- Fit each of the methods to the training data.
- Predict the left-out World Cup using each of the prediction methods.
- Iterate steps 1–3 such that each World Cup is once the left-out one.
- Compare predicted and real outcomes for all prediction methods.
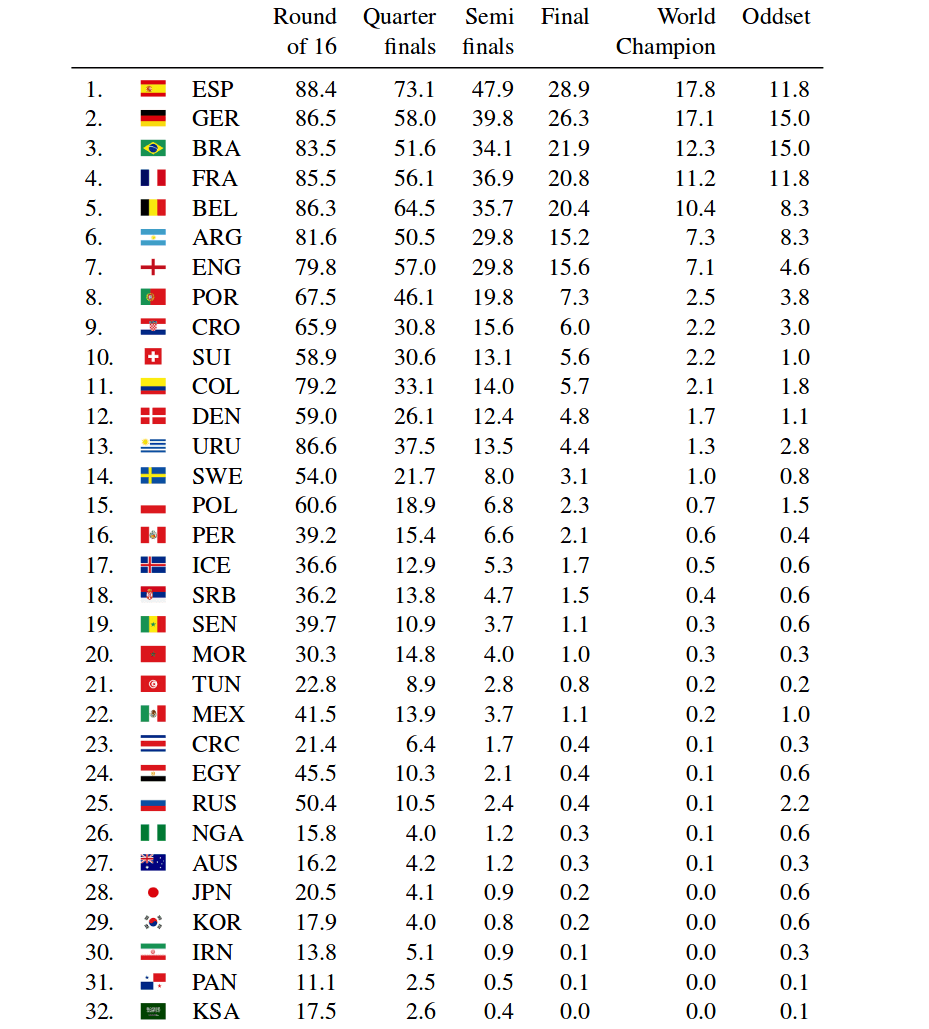
This method of leave-one-out ensures that each match of the dataset is once part of the test set. The comparison of all three methods are given in the tables and also a comparison with the bookmakers’ performance.

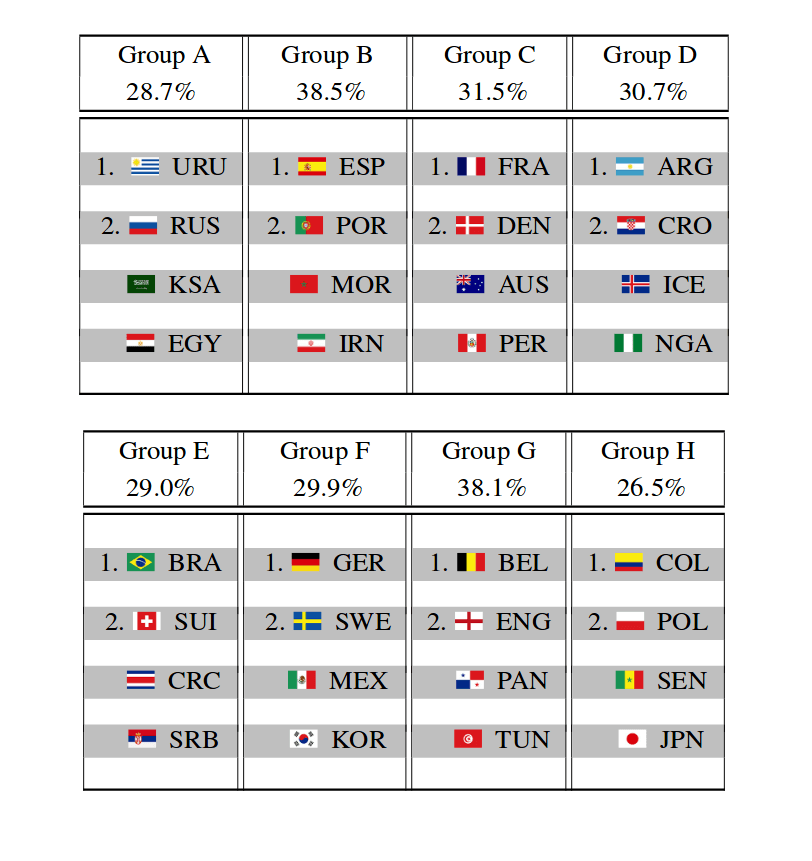
Finally, since everyone wants to know the winner, the random forest prediction is Spain! The method slightly favors Spain before the defending champion Germany and Brazil. The researchers run the simulation and give the prediction for the group stage outcome, the individual matches in the knockout phase as well as probabilities for each team to reach some of the stages in the World Cup.
P.S. Since the Spanish coach was fired yesterday, it seems like Germany should be on the top, Brazil and France next.
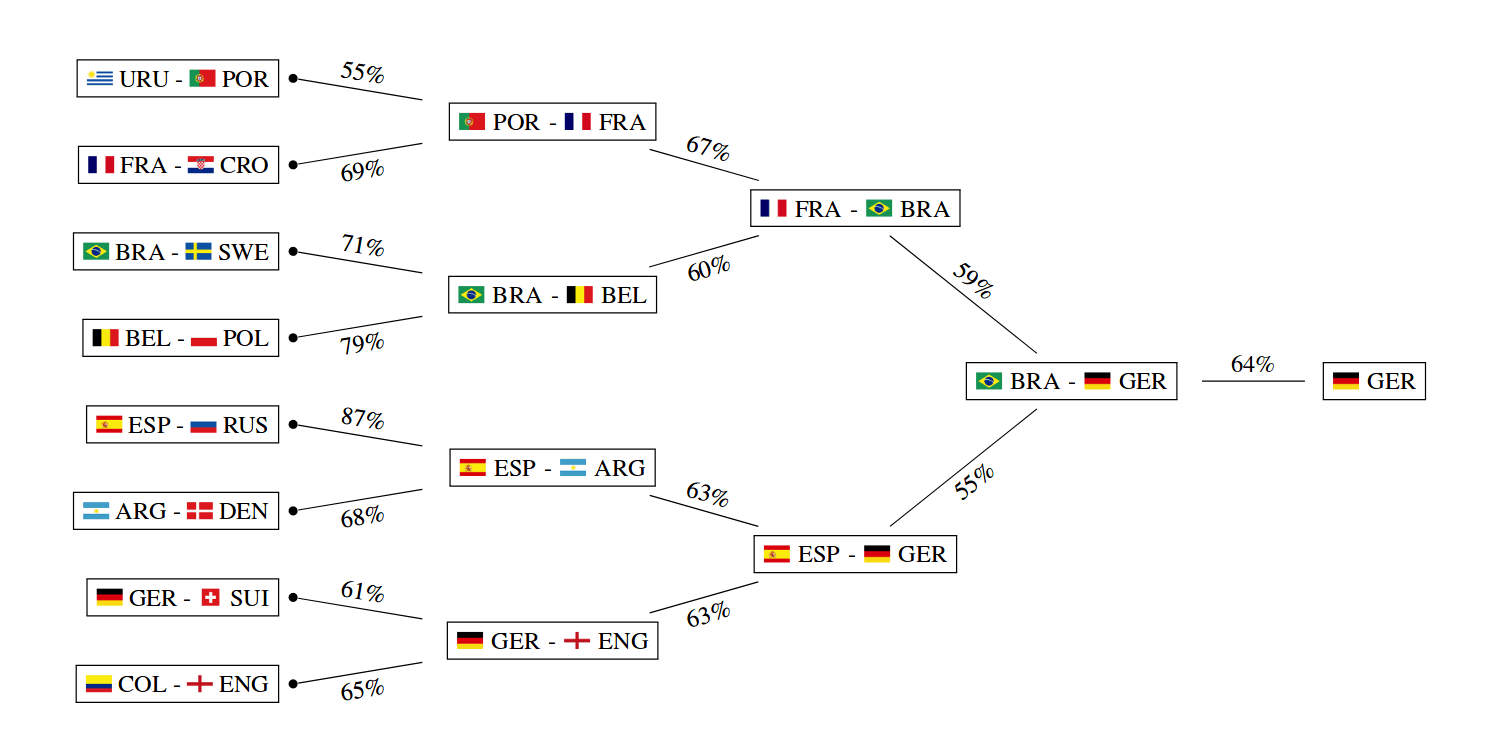
By doing 100 000 simulations they provide a most probable tournament course. According to the most probable tournament course, instead of the Spanish, the German team would win the World Cup with the highest rate.
May be interesting: