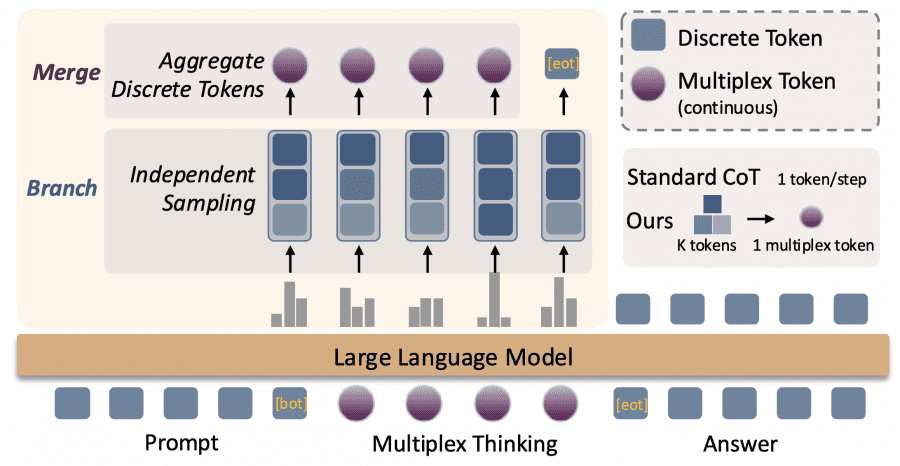
Researchers from the University of Pennsylvania and Microsoft Research introduced Multiplex Thinking — a new reasoning method for large language models. The idea is to generate not one token at each step, but several at once, combining them into a special “multiplex token”. This allows the model to keep multiple probable solution paths in memory simultaneously, like a human considering different action options in parallel.
DeepSeek-R1-Distill-Qwen models with 1.5B and 7B parameters, trained with Multiplex Thinking, solve 2.5% more olympiad-level math problems at Pass@1 and show growth from 40% to 55% at Pass@1024. The project is open-source — code and model checkpoints are available on GitHub.
Standard Chain-of-Thought works like depth-first search: the model chooses one token, then the next, and so on along a single path. If it makes a mistake early on, the entire path becomes useless. Multiplex Thinking is more like breadth-first search: the model simultaneously explores K different continuation options at each step, without increasing sequence length.
How Multiplex Thinking Works
At each reasoning step, the model doesn’t select one token from the probability distribution, but independently samples K tokens. For example, if K=3, the model can choose three different words with high probabilities. These tokens are then converted into embeddings (vector representations) and combined into one continuous multiplex token through weighted averaging.
The key feature is adaptability. When the model is confident about the next step (low entropy distribution), all K samples will likely coincide, and the multiplex token essentially becomes a regular discrete token. When the model is uncertain (high entropy), the K samples will differ, and the multiplex token will encode information about multiple paths simultaneously.
Importantly, the probability of a specific multiplex token can be calculated: it’s the product of probabilities of all K sampled tokens. This allows direct optimization through reinforcement learning (RL), which is impossible for deterministic continuous thinking methods like Soft Thinking.
Experimental Results
The method was tested on six challenging mathematical datasets: AIME 2024, AIME 2025, AMC 2023, MATH-500, Minerva Math, and OlympiadBench. DeepSeek-R1-Distill-Qwen models with 1.5B and 7B parameters were used as base models. Training was conducted using GRPO (Group Relative Policy Optimization) on the DeepScaleR-Preview dataset of approximately 40,000 problem-answer pairs.
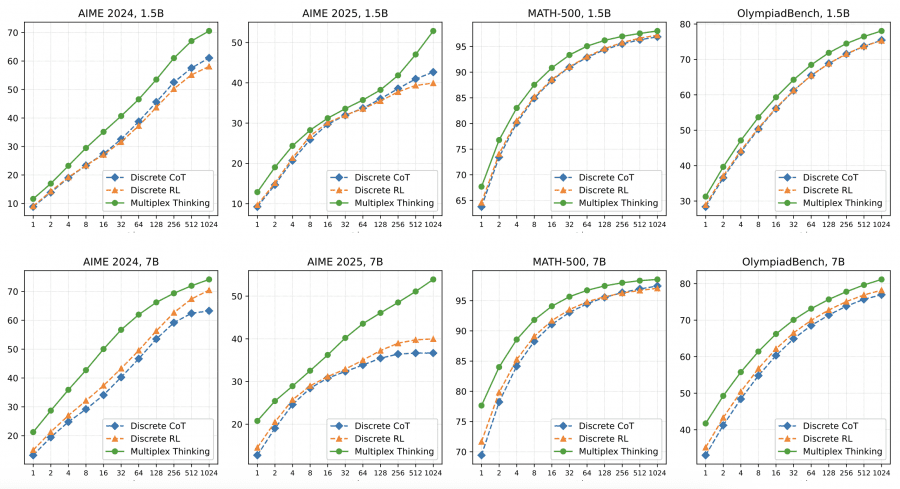
By Pass@1 metric with top-p=0.95, Multiplex Thinking won in 11 out of 12 experimental configurations. On the 7B model, the method showed particularly strong results: 20.6% on AIME 2024 versus 17.2% for discrete RL, 50.7% on AMC 2023 versus 44.7%, and 78.0% on MATH-500 versus 74.1%. This means improvements come from the multiplex representation itself, not just from RL training.
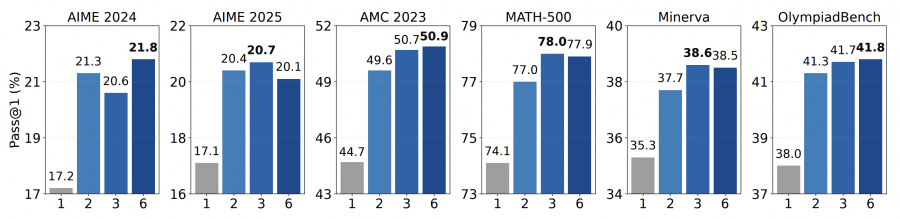
When increasing attempts to Pass@1024, the gap becomes even larger. On AIME 2025 (7B), discrete RL plateaus around 40%, while Multiplex Thinking continues improving to 55%. This shows the method better explores the solution space and finds correct answers even in complex tasks with sparse solution spaces.
Why It Works
Researchers analyzed policy entropy during training. It turned out that with discrete RL, entropy drops by 9.44% from start to end of training — the model quickly becomes confident in choosing the same paths. With Multiplex Thinking, the entropy drop is only 5.82-7.09% depending on K. This means the method helps the model maintain exploration diversity longer, without “getting stuck” on one solution variant.
An important point is token efficiency. Multiplex Thinking generates shorter sequences with the same or better accuracy. On average, response length is about 3400 tokens versus 3600 for discrete RL. This happens because one multiplex token carries more information than a regular discrete token — it encodes multiple continuation options simultaneously.
Experiments with different multiplex widths K (number of samples per step) showed an interesting pattern. The transition from K=1 (regular discrete token) to K=2 provides substantial gains — for example, on AMC 2023 accuracy jumps from 44.7% to 49.6%. Further increases to K=3 and K=6 show smaller effects. The optimal value turned out to be K=3, which balances exploration diversity and computational costs.
Comparison with Other Methods
Multiplex Thinking was compared with three types of baseline methods. Discrete CoT is regular chain-of-thought generation without additional training. Stochastic Soft Thinking is a recent continuous thinking method that adds stochasticity through Gumbel-Softmax. Discrete RL is discrete reinforcement learning on the same dataset with the same hyperparameters.
Interestingly, even the version without training (Multiplex Thinking-I) showed competitive results. On the 7B model, it outperformed Discrete CoT on all datasets and was nearly on par with Stochastic Soft Thinking. This proves that the multiplex representation itself provides inherent benefits for reasoning, independent of RL optimization.
When comparing computational costs, Multiplex Thinking-I with a 4096 token limit performs as well as Discrete CoT with a 5120 token limit. This means the multiplex approach saves 20% sequence length while maintaining quality.
How the Model Chooses When to Explore
Visualization of actual reasoning trajectories revealed an interesting pattern. The model naturally alternates between “consensus” and “exploration” phases. In consensus phases, all K samples coincide — the model is confident about the next step. In exploration phases, samples differ — the model sees multiple plausible options and encodes them all into one multiplex token.

Exploration phases correspond to high-entropy steps where multiple continuations compete. This aligns with recent research showing that high-entropy “fork tokens” play a critical role in reasoning and provide the main gains from RLVR (reinforcement learning with verifiable rewards).
Formally, the entropy of a multiplex token is K times larger than the entropy of a single discrete sample: H(K_i) = K · H(π_θ(q, c_{<i})). This means exponential expansion of the effective exploration volume from |V| to |V|^K, where V is the vocabulary size. The model can postpone discrete decisions and preserve probabilistic diversity within the reasoning trajectory.
Technical Details and Limitations
Training was conducted for 300 steps with a global batch size of 128 questions, learning rate 1×10^-6, without KL penalty and entropy penalty. During training, 8 rollouts per question were generated with temperature 1.0 and top-p 1.0. For evaluation, top-p 0.95 was used with averaging over 64 runs. The Pass@k metric was calculated through bootstrapping 1000 times over 1024 runs.
The thinking stopping criterion is when the discrete token with highest probability among K samples is the special token . Researchers deliberately avoided heuristics like tracking sequences of low-entropy tokens, because the model starts exploiting these rules during RL training, leading to instability and generation of meaningless content.
Two token aggregation strategies showed comparable results: simple embedding averaging and weighted averaging by probabilities from the LM head. This suggests that the method’s effectiveness comes from including diverse reasoning paths in the latent space, rather than the specific way they’re combined.
The method is implemented on top of the verl framework and SGLang version 0.4.9.post6. All experiments were run on 8× NVIDIA DGX B200 GPUs with bfloat16 precision. The evaluation platform code and examples are available on GitHub for the community to reproduce results.
Main takeaway: Multiplex Thinking successfully combines the advantages of discrete sampling and continuous representations. The method preserves the stochasticity necessary for effective RL, while compressing information about multiple reasoning paths into compact sequences. This opens a path to more efficient scaling of test-time compute for reasoning tasks.