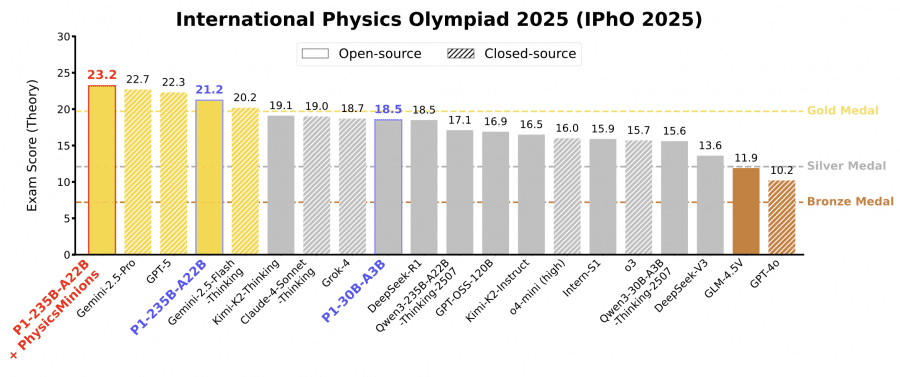
P1-235B-A22B from Shanghai AI Laboratory became the first open-source model to win a gold medal at the latest International Physics Olympiad IPhO 2025, scoring 21.2 out of 30 points and ranking third after Gemini-2.5-Pro and GPT-5. This is quite an unexpected result for an open-source model. The P1-30B-A3B version also showed excellent results—earning a silver medal at IPhO 2025, surpassing virtually all other open-source models. Combined with the PhysicsMinions agent system, P1-235B-A22B took first place at IPhO 2025. The P1 model family and weights are published as open source on Github and HuggingFace.
What is P1 and Why It Matters
AI has taken an important step: from simple puzzle-solving to genuine scientific reasoning. Now it’s not just about getting an answer that passes the criteria, but finding a solution that actually works according to the laws of physics.
Physics is the strictest test of this capability because it fundamentally connects abstract symbols with reality and serves as the foundation for most modern technologies.
Mastering physics requires more than memorizing facts or applying formulas—it demands conceptual understanding, system decomposition, and precise multi-step reasoning based on physical laws. These skills are most rigorously tested at olympiads such as the International Physics Olympiad (IPhO), where solving each problem requires both analytical precision and creative approach.
Researchers created P1—a family of models trained entirely through reinforcement learning (RL) based on Qwen3 models with extended thinking mode. P1-30B-A3B was trained on top of Qwen3-30B-A3B-Thinking-2507, while P1-235B-A22B was trained on Qwen3-235B-A22B-Thinking-2507. The models combine train-time scaling—improvement during training through RL, and test-time scaling—adaptive deployment through agent control during inference.
Training Dataset
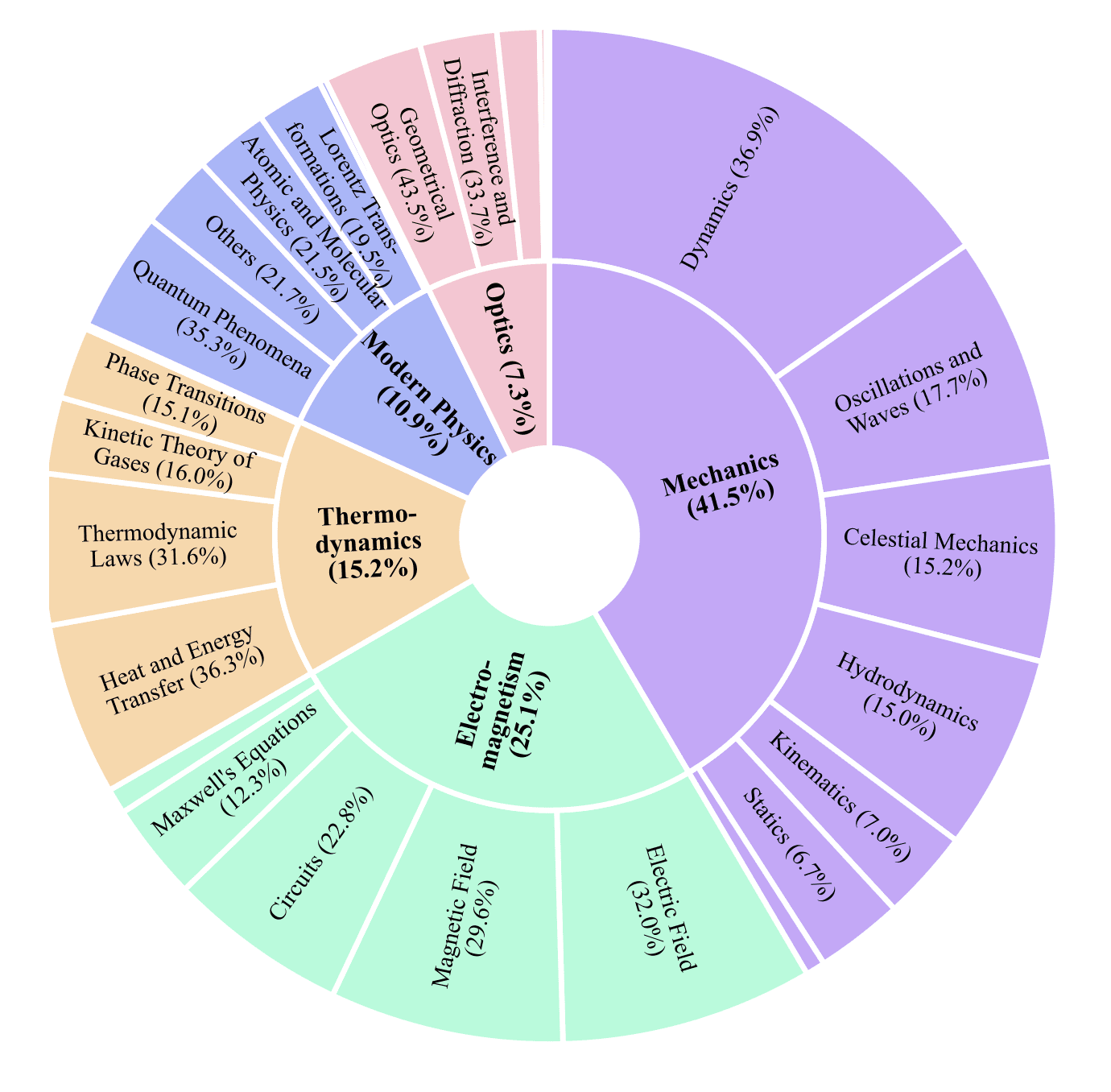
For P1 training, researchers collected a specialized dataset of 5,065 text-based olympiad-level physics problems. The dataset includes 4,126 problems from physics olympiads and 939 problems from competition textbooks, covering 5 fields of physics and 25 subfields. Instead of pursuing broad coverage, researchers focused on depth and rigor—physics olympiads uniquely combine abstract reasoning with empirical laws, providing a demanding training dataset for improving and evaluating model reasoning capabilities within physical constraints.
Each sample in the dataset follows a structured Question-Solution-Answer schema with metadata. Problem formulations are preserved in their original form whenever possible. Solutions are written by physics experts, providing authentic reasoning trajectories. Verifiable final answers provide unambiguous correctness criteria necessary for Reinforcement Learning with Verifiable Rewards (RLVR). Annotations of type, units of measurement, and scoring points support reliable validation and reflect weighted human grading criteria. Each sample is tagged with physics field and source, enabling analysis of domain coverage and studying the impact of data provenance on training dynamics.
Training Approach
P1 is trained through a multi-stage reinforcement learning (RL) framework. Researchers formulate the task of solving olympiad physics problems as a Markov Decision Process (MDP), where the state is the model context (including problem formulation and all previously generated reasoning steps), the action is the next token from the vocabulary, and the reward function evaluates the correctness and quality of the final solution.
For optimization, Group Sequence Policy Optimization (GSPO) is used—a method that elevates optimization from token level to sequence level, using length-normalized sequence likelihood importance ratios. This helps reduce variance and improve training stability.
Reward Function Design
Following the “correct-or-not” design in RLVR methods, researchers use a binary reward scheme based on answer correctness. However, physics problems often include multiple sub-questions or require multiple final results. To account for this structure, test-case-style reward aggregation is applied, similar to program evaluation: final reward R = (1/N) × Σr_i, where N is the number of required sub-answers in the problem, and r_i is the correctness indicator for the i-th sub-answer.
Verifier Design
To handle the inherent complexity of physics answers, which often appear as symbolic expressions rather than single numeric values, researchers implemented a hybrid verification framework integrating both rule-based and model-based components. The rule-based verifier combines symbolic computation with rule-based checks using SymPy and math-verify heuristics. The model-based verifier uses the large language model Qwen3-30B-A3B-Instruct-2507 as an answer-level verifier, improving robustness in cases challenging for purely symbolic methods.
Training Stabilization Mechanisms
Training through reinforcement learning often faces a problem: the model improves quickly at first, but then hits a “ceiling” and stops learning. This happens due to entropy collapse, sparse rewards, or poor data quality.
Researchers devised two ways to solve this problem. First—dataset filtering before training. They remove tasks that are too easy (which the model solves in 70%+ cases) and too difficult (which aren’t solved at all), keeping only those on which the model can actually learn. The second method is dynamic expansion of the search space as the model becomes smarter: increasing the number of attempts per task and maximum answer length.
Training Stabilization
An infrastructure problem was discovered. Modern RL systems separate processes for performance: fast engines (vllm, SGLang) generate model responses, while heavy training systems (Megatron) update weights. But they work with different numerical precision and use different computational optimizations. As a result, the same operation produces slightly different results in the two systems—and this accumulates, creating noise in gradients. The Truncated Importance Sampling method solves the problem by recalculating weights accounting for these discrepancies.
Physics Olympiad Results
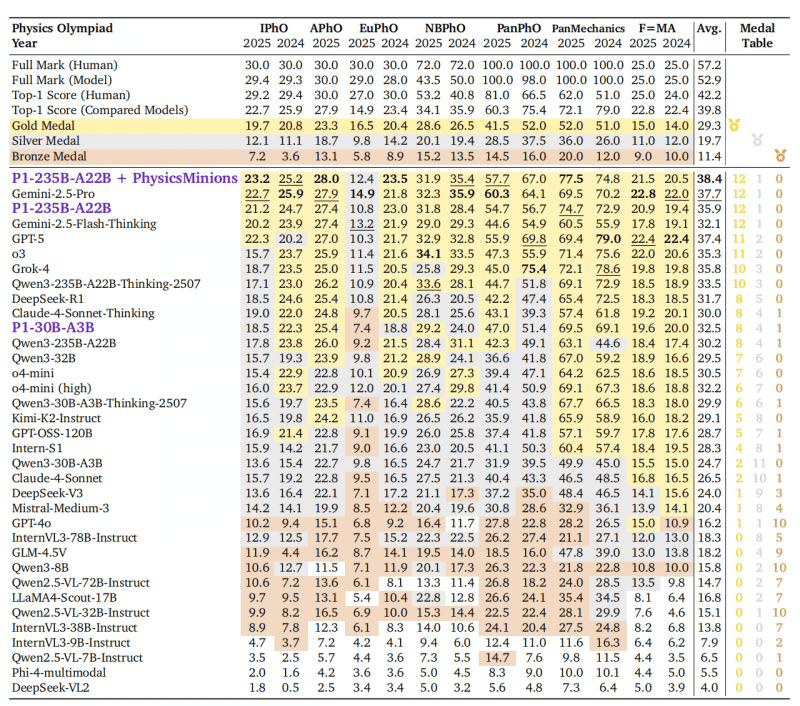
To evaluate P1, researchers used the HiPhO benchmark—a collection of 13 recent physics olympiads from 2024-2025, from international to regional levels.
P1-235B-A22B showed outstanding results: scored 21.2 out of 30 points at the International Physics Olympiad (IPhO 2025) and ranked 3rd in the world—after Gemini-2.5-Pro (22.7) and GPT-5 (22.3). This is the first open-source model to receive a gold medal at IPhO 2025. In total, across 13 olympiads, the model won 12 gold and 1 silver medal, surpassing proprietary models Grok-4 and Claude-4-Sonnet-Thinking.
P1-30B-A3B, the smaller version, earned silver at IPhO 2025, ranking 8th out of 35 tested models. It surpassed nearly all other open-source models, including comparable-sized Qwen3-32B and Qwen3-30B-A3B-Thinking-2507, demonstrating high training efficiency.
Agent Enhancement
Combined with the PhysicsMinions agent system, P1’s average result improves from 35.9 to 38.4 points, placing the model in first place among all models, ahead of Gemini-2.5-Pro (37.7) and GPT-5 (37.4).
PhysicsMinions includes three interacting components: Visual Studio for visual analysis, Logic Studio for logical reasoning, and Review Studio for solution verification. The system implements iterative reflection—P1 can reason, critique its own solutions, and improve them, similar to how research physicists work.
P1 Generalizability
Researchers conducted post-training on a specialized dataset to improve physics problem-solving abilities. Beyond improvements in the specific domain, they additionally investigated: does the P1 model maintain or even enhance its general reasoning ability in mathematics, STEM, and programming domains? P1 models were compared with their corresponding base models on diverse benchmarks: six mathematical datasets (AIME24, AIME25, HMMT, IMO-AnswerBench, AMOBench, BeyondAIME), two STEM-oriented assessments (GPQA, HLE), one programming benchmark (LiveCodeBench), and a general reasoning task (LiveBench).
Notably, P1 models consistently demonstrate advantages over their base counterparts: P1-30B-A3B outperforms Qwen3-30B-A3B-Thinking-2507 across all metrics, while P1-235B-A22B achieves superior performance compared to Qwen3-235B-A22B-Thinking-2507 in most categories. This pattern underscores that P1 models not only maintain but enhance general reasoning capabilities beyond the target domain—even on more challenging mathematical benchmarks (e.g., IMO-AnswerBench, AMOBench) that test advanced problem-solving skills.
These results suggest that domain-focused post-training can induce transferable improvements in general reasoning. Researchers hypothesize two contributing factors. First, the optimization process refines reasoning trajectories in a way that transcends domain boundaries, enabling strategies beneficial for mathematics, STEM, and programming tasks to emerge. Second, the training dataset, while specialized, shares structural similarities with other domains—such as rigorous symbolic manipulation, multi-step logical deduction, and abstract problem modeling—that underlie general reasoning.
Important Lesson About Verifiers
Due to the difficulty of implementing a comprehensive and fully correct verification mechanism based exclusively on rules, researchers developed a hybrid verifier integrating both rule-based and model-based reasoning to achieve broader coverage. However, they found that applying a model-based verifier directly in the post-training process can be risky.
When comparing training dynamics with and without a model-based verifier, it’s observed that the variant using a model-based verifier exhibits explosive growth in response length, but its validation performance deteriorates compared to the setup using only a rule-based verifier.
Researchers attribute this phenomenon to two main causes:
- The model-based verifier is susceptible to hacking by the policy model. Since the verifier itself is a language model, it may develop unintended biases, favoring atypical response patterns such as overly verbose or stylistically peculiar answers, which can be exploited by the policy model to obtain artificially high rewards.
- The negative impact of false positives—incorrectly rewarding wrong answers—is substantially more detrimental than false negatives—missing some correct responses.
This can be understood in terms of verification precision and verification recall. The rule-based verifier typically offers high precision but limited recall, while the model-based verifier increases recall at the expense of precision. During reinforcement learning, this imbalance can easily destabilize optimization: a few highly-rewarded false positives can dominate the learning signal, steering the policy toward degenerate solution patterns.
Conclusions
P1 represents a significant step toward LLMs that can engage in genuine scientific reasoning and ultimately contribute to the frontier of physics research. P1’s success in mastering olympiad-level physics represents a key milestone: if models can rigorously solve well-defined problems grounded in natural laws, they may eventually contribute to exploring uncharted scientific frontiers.
The team released two versions of P1 models and evaluated them on HiPhO—a new benchmark aggregating the latest 13 olympiad exams from 2024-2025. The flagship model P1-235B-A22B achieves a milestone for the open-source community—becoming the first open model to reach gold-medal performance at IPhO 2025, earning 12 gold and 1 silver across the full HiPhO suite. The lightweight variant P1-30B-A3B achieves silver-medal performance at IPhO 2025, surpassing virtually all previous open baselines.
Combined with the PhysicsMinions agent system, P1 achieves overall No.1 ranking on both IPhO 2025 and HiPhO leaderboards.
Beyond physics, P1 models demonstrate remarkable generalizability. The 30B variant significantly outperforms its base model (Qwen3-30B-A3B-Thinking-2507) across seven benchmarks of mathematics, programming, and general reasoning, suggesting that physics post-training cultivates transferable reasoning skills rather than domain overfitting.