Исследователи из Google AI предлагают новый подход для обучения моделей с подкреплением. Подход позволяет использовать алгоритмы, которые избегают использование грубых аппроксимаций при переходе от математического обоснования к практической реализации. Предложенный метод основывается на двойственности (дуальности) выпуклых функций. Это математический инструмент для трансформирования задач из одной формы в эквивалентные задачи других форм, которые менее вычислительно сложные. В случае с RL дуальность применяется, чтобы трансформировать традиционную постановку задачи ограничение-удовлетворение в более удобную для практического применения форму.
Описание проблемы
Многие современные RL-алгоритмы, как Q-learning и актор-критик, предлагают сводит задачу RLL к проблеме ограничение-удовлетворение. Ограничение существует для каждого возможного состояния среды. Например, в навигации робота, основанной на зрении, состояния среды соотносятся с каждым возможным изображением с камеры.
Несмотря на то, что подход ограничения-удовлетворения является наиболее популярным, такую стратегию сложно масштабировать на реальный мир, где сложность задачи значительно возрастает. В практическом применении RL-алгоритмов, как навигация робота, пространство состояний часто несчетное. Имплементации Q-learning и actor-critic подходов игнорируют математические ограничения или избавляются от них с помощью аппроксимации.
Как работает подход с двойственностью
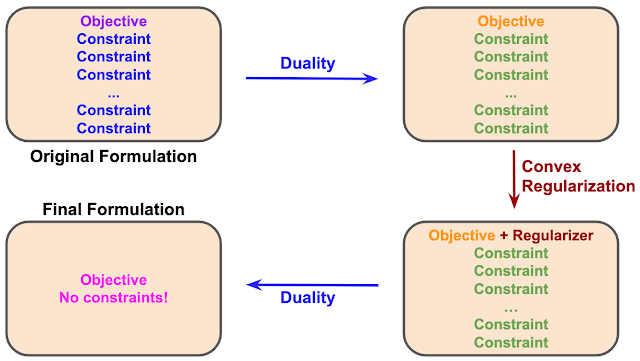
В предложенном подходе задача обучения с подкреплением формулируется сначала как математическая целевая функция с набором ограничений. При этом количество ограничений может быть бесконечно. С помощью принципа двойственности изначальная формулировка задачи трансформируется в альтернативную, которая более вычислительно простая. Так, формат задачи остается тем же, — одна целевая функция с набором ограничений, — но сама целевая функция с ограничениями меняется.
Затем дуальная целевая функция аугментируется с помощью регуляризатора выпуклости. Такой регуляризатор используется в задачах оптимизации, чтобы сделать задачу более гладкой и простой для решения. На итоговом шаге дуальность применяется еще раз. На выходе получается другая эквивалентная формулировка задачи. На итоговом шаге также используется регуляризатор (f-regularizer).
Несмотря на то, что использование принципа двойственности меняет формулировку задачи, это не меняет ее оптимального решения. Значит, на то, к чему сойдется алгоритм, предложенный подход не влияет. При этом подход позволяет упростить процесс обучения алгоритмов с подкреплением.
Оценка работы подхода
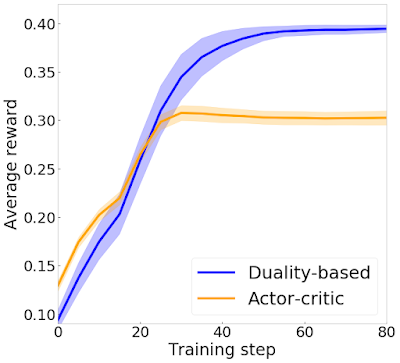
Исследователи сравнивают предложенный подход с state-of-the-art методом для обучения моделей с подкреплением, actor-critic архитектурой. Ниже видно, что алгоритм с дуальностью после определенного порога обучающих шагов получает в среднем большее количество наград, чем подход с актор-критик архитектурой.