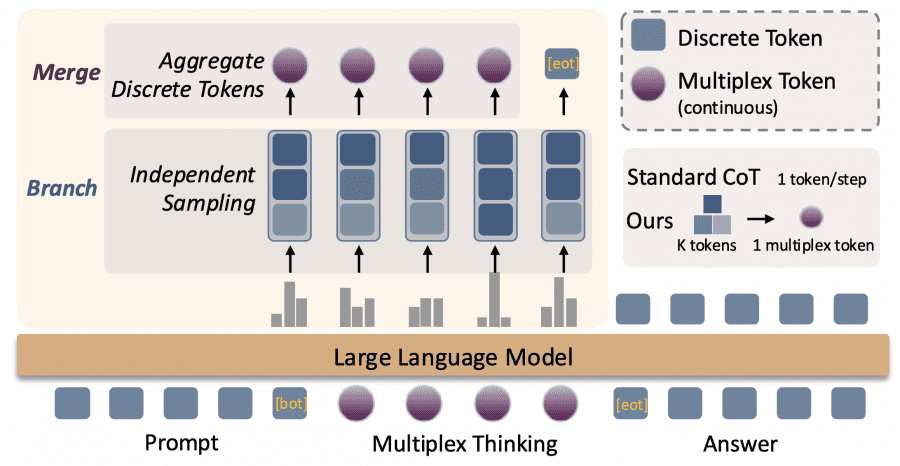
Исследователи из Университета Пенсильвании и Microsoft Research представили Multiplex Thinking — новый метод рассуждения для больших языковых моделей. Идея в том, чтобы на каждом шаге генерировать не один токен, а сразу несколько, объединяя их в специальный «мультиплексный токен». Это позволяет модели держать в памяти несколько вероятных путей решения одновременно, как человек, который рассматривает разные варианты действий параллельно.
Модели DeepSeek-R1-Distill-Qwen размером 1.5B и 7B параметров, обученные с Multiplex Thinking, решают на 2.5% больше олимпиадных математических задач при Pass@1 и показывают рост с 40% до 55% при Pass@1024. Проект открытый — код и чекпоинты моделей доступны на GitHub.
Обычный Chain-of-Thought (цепочка рассуждений) работает как поиск в глубину: модель выбирает один токен, потом следующий, и так далее по одному пути. Если она ошиблась на раннем этапе, весь путь становится бесполезным. Multiplex Thinking больше похож на поиск в ширину: модель одновременно исследует K разных вариантов продолжения на каждом шаге, но при этом не увеличивает длину последовательности.
Как работает мультиплексное мышление
На каждом шаге рассуждения модель не выбирает один токен из распределения вероятностей, а независимо семплирует K токенов. Например, если K=3, модель может выбрать три разных слова с высокими вероятностями. Затем эти токены превращаются в эмбеддинги (векторные представления) и объединяются в один непрерывный мультиплексный токен через взвешенное усреднение.
Ключевая особенность — адаптивность. Когда модель уверена в следующем шаге (низкая энтропия распределения), все K семплов скорее всего совпадут, и мультиплексный токен фактически превращается в обычный дискретный токен. А когда модель не уверена (высокая энтропия), K семплов будут разными, и мультиплексный токен закодирует информацию сразу о нескольких путях.
Важно, что вероятность конкретного мультиплексного токена можно посчитать: это произведение вероятностей всех K семплированных токенов. Это позволяет напрямую оптимизировать модель через обучение с подкреплением (RL), что невозможно для детерминистических методов непрерывного мышления вроде Soft Thinking.
Результаты экспериментов
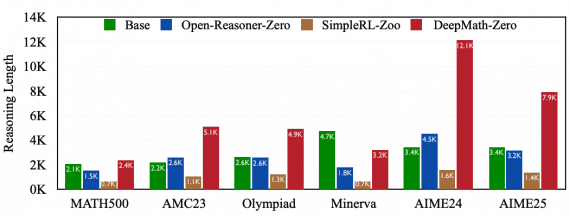
Метод тестировали на шести сложных математических датасетах: AIME 2024, AIME 2025, AMC 2023, MATH-500, Minerva Math и OlympiadBench. В качестве базовых моделей использовали DeepSeek-R1-Distill-Qwen размером 1.5B и 7B параметров. Обучение проводилось методом GRPO (Group Relative Policy Optimization) на датасете DeepScaleR-Preview из примерно 40,000 пар задача-ответ.
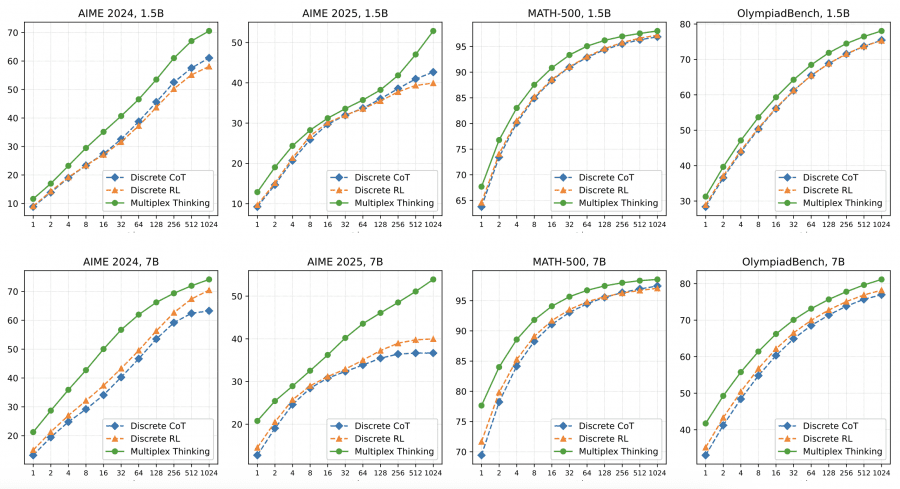
По метрике Pass@1 с top-p=0.95 Multiplex Thinking победил в 11 из 12 экспериментальных конфигураций. На модели 7B метод показал особенно сильные результаты: 20.6% на AIME 2024 против 17.2% у дискретного RL, 50.7% на AMC 2023 против 44.7%, и 78.0% на MATH-500 против 74.1%. Это означает, что улучшения приходят именно от мультиплексного представления, а не просто от RL-обучения.
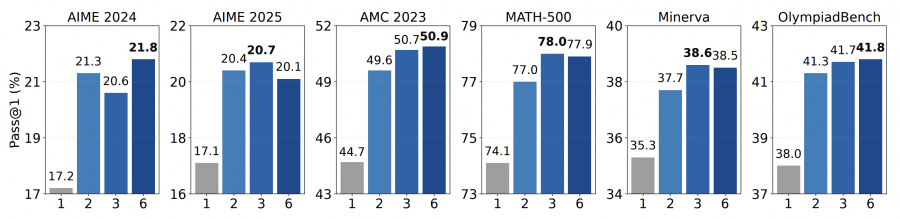
При увеличении количества попыток до Pass@1024 разрыв становится ещё больше. На AIME 2025 (7B) дискретный RL выходит на плато около 40%, а Multiplex Thinking продолжает улучшаться до 55%. Это показывает, что метод лучше исследует пространство решений и находит правильные ответы даже в сложных задачах с разреженным пространством решений.
Почему это работает
Исследователи провели анализ энтропии политики во время обучения. Оказалось, что при дискретном RL энтропия падает на 9.44% от начала к концу обучения — модель быстро начинает уверенно выбирать одни и те же пути. С Multiplex Thinking падение энтропии составляет всего 5.82-7.09% в зависимости от K. Это значит, что метод помогает модели дольше сохранять разнообразие в исследовании, не «залипая» на одном варианте решения.
Важный момент — эффективность по токенам. Multiplex Thinking генерирует более короткие последовательности при той же или лучшей точности. В среднем длина ответа составляет около 3400 токенов против 3600 у дискретного RL. Это происходит потому, что один мультиплексный токен несёт больше информации, чем обычный дискретный токен — он кодирует сразу несколько вариантов продолжения.
Эксперименты с разной шириной K (количество семплов на шаг) показали интересную закономерность. Переход от K=1 (обычный дискретный токен) к K=2 даёт существенный прирост — например, на AMC 2023 точность подскакивает с 44.7% до 49.6%. Дальнейшее увеличение до K=3 и K=6 даёт меньший эффект. Оптимальным оказалось значение K=3, которое балансирует между разнообразием исследования и вычислительными затратами.
Сравнение с другими методами
Multiplex Thinking сравнивали с тремя типами базовых методов. Discrete CoT — это обычная генерация цепочки рассуждений без дополнительного обучения. Stochastic Soft Thinking — недавний метод непрерывного мышления, который добавляет стохастичность через Gumbel-Softmax. Discrete RL — дискретное обучение с подкреплением на том же датасете и с теми же гиперпараметрами.
Интересно, что даже версия без обучения (Multiplex Thinking-I) показала конкурентные результаты. На модели 7B она обошла Discrete CoT на всех датасетах и была практически наравне со Stochastic Soft Thinking. Это доказывает, что само мультиплексное представление несёт внутреннюю пользу для рассуждения, независимо от RL-оптимизации.
При сравнении вычислительных затрат выяснилось, что Multiplex Thinking-I с лимитом в 4096 токенов работает так же хорошо, как Discrete CoT с лимитом 5120 токенов. То есть мультиплексный подход позволяет сэкономить 20% длины последовательности при сохранении качества.
Как модель выбирает, когда исследовать
Визуализация реальных траекторий рассуждения показала интересный паттерн. Модель естественным образом чередует фазы «консенсуса» и «исследования». В фазе консенсуса все K семплов совпадают — модель уверена в следующем шаге. В фазе исследования семплы различаются — модель видит несколько правдоподобных вариантов и кодирует их все в один мультиплексный токен.

Фазы исследования соответствуют шагам с высокой энтропией, где несколько продолжений конкурируют между собой. Это согласуется с недавними исследованиями, показывающими, что именно высокоэнтропийные «токены-развилки» играют критическую роль в рассуждении и дают основной прирост от RLVR (обучения с подкреплением с верифицируемыми наградами).
Формально энтропия мультиплексного токена в K раз больше энтропии одного дискретного семпла: H(K_i) = K · H(π_θ(q, c_{<i})). Это означает экспоненциальное расширение эффективного объёма исследования с |V| до |V|^K, где V — размер словаря. Модель может отложить дискретное решение и сохранить вероятностное разнообразие внутри траектории рассуждения.
Технические детали и ограничения
Обучение проводилось 300 шагов с глобальным batch size 128 вопросов, learning rate 1×10^-6, без KL-пенализации и энтропийной пенализации. Во время обучения генерировалось 8 роллаутов на вопрос с температурой 1.0 и top-p 1.0. Для оценки использовался top-p 0.95 с усреднением по 64 запускам. Метрика Pass@k вычислялась через бутстрэппинг 1000 раз на 1024 запусках.
Критерий остановки мышления — когда дискретный токен с наибольшей вероятностью среди K семплов оказывается специальным токеном . Исследователи сознательно отказались от эвристик вроде отслеживания серии низкоэнтропийных токенов, потому что модель начинает эксплуатировать эти правила во время RL-обучения, что приводит к нестабильности и генерации бессмысленного контента.
Две стратегии агрегации токенов показали сравнимые результаты: простое усреднение эмбеддингов и взвешенное усреднение по вероятностям из LM head. Это говорит о том, что эффективность метода идёт от включения разнообразных путей рассуждения в латентное пространство, а не от конкретного способа их комбинирования.
Метод реализован на базе фреймворка verl и SGLang версии 0.4.9.post6. Все эксперименты выполнялись на 8× NVIDIA DGX B200 GPU с точностью bfloat16. Код платформы оценки и примеры доступны на GitHub, чтобы сообщество могло воспроизвести результаты.
Главный вывод: Multiplex Thinking успешно объединяет преимущества дискретного семплирования и непрерывных представлений. Метод сохраняет стохастичность, необходимую для эффективного RL, но при этом сжимает информацию о множестве путей рассуждения в компактные последовательности. Это открывает путь к более эффективному масштабированию вычислений во время инференса (test-time compute) для задач, требующих рассуждения.