Разработан новый алгоритм классификации без отрицательных данных в датасете
29 ноября 2018
Разработан новый алгоритм классификации без отрицательных данных в датасете
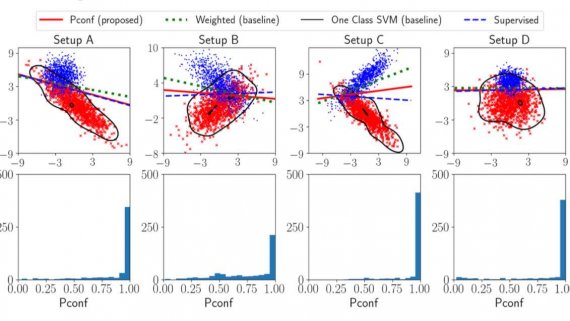
Исследователи проекта RIKEN разработали новый метод машинного обучения, который позволяет обучать модели классифицировать объекты без отрицательных данных в обучающем датасете. В задачах классификации алгоритмы используют положительные и отрицательные данные. Например,…