When we use a camera, we want the recorded image to be a faithful representation of what we see in front of us. However, very often images contain blur, and one of the major sources of blur is the camera or object motion. This blur is commonly known as motion blur, and in the past, there have been many attempts to remove the blur and reconstruct a sharp image.
Blurring and de-blurring?
The convolution operation is the process of applying a general purpose filter to an image (by applying a function using a kernel or convolution matrix to local receptive fields of the image). De-blurring, in essence, is trying to reverse convolution on an image (and it is often called deconvolution). This all comes from the fact that the complex image formation process generates an image and de-blurring is trying to remove the blur introduced to the image during this process.
There are two types of approaches generally, to image de-blurring: methods based on blind deconvolution and techniques based on non-blind deconvolution. Blind deconvolution refers to deconvolving the image without the explicit knowledge of the impulse response function, used in the convolution. The methods relying on blind de-convolution often make appropriate assumptions to estimate the impulse response function, while the others rely on the assumption that the kernel (the impulse response function) is known.

New de-blurring approach
Arguing that many of the previously existing approaches assume an over-simplistic image formation model, researchers from the Université Paris-Saclay and Universidad de la República propose a novel de-blurring method based on non-blind deconvolution. In their paper, named “Modeling realistic degradations in non-blind deconvolution,” they tackle the problem of motion de-blurring in images by giving a more realistic (and more complex) image formation model.
Starting from the simplest image acquisition model, which takes into account: the ideal non-blurred (sharp) image, the blurring kernel and a realization of Gaussian noise, the authors propose an extended, more realistic formation model. The simplest model used very often in many approaches is given as a linear combination of the sharp image, the kernel, and the noise. However, the authors argue that it is not powerful enough to capture the process of generating an image and modeling a realistic image acquisition pipeline. As they explain, this is due to non-invertible, non-linear degradations that can occur along the whole formation pipeline. Examples of these degradations addressed with the proposed model are saturation, quantization, and gamma correction.
In the novel approach, the authors approximate the motion blurring function with a model that includes pixel saturation operator, pixel quantization function and a gamma correction coefficient. Since imposing a model itself is not enough to solve a problem (especially of this degree), the authors also present a deconvolution method that works under real practical degradations. The technique is a non-blind deconvolution, so it assumes knowledge of the kernel function.

The method
To explain it simply, the whole de-blurring method is based on defining each degradation as energy (that expresses the data fitting between the ideal (sharp) image and the blurred one) that is minimized using the Stochastic Deconvolution framework.
Based on coordinate descent algorithm, which is derivative-free and it can be used to minimize any energy (cost) minimization problem, the method is reducing the defined energies for the three image degradations: pixel saturation, quantization, and gamma correction.
In the paper, separate data fitting terms (defining the cost or energy) are given for the three degradations, and finally, a combined one is proposed that addresses the problem from the viewpoint of all three (realistic) degradations.
Experiments and Evaluation
The authors study each of the separate models for the degradations mentioned before (except the gamma correction). They apply the method to images from the dataset BSDS300 and calculate and record PSNR (peak signal-to-noise ratio) as an evaluation metric. They show that their models outperform the previous approaches.
To evaluate the complete method, tackling all three degradations at once, the authors created a realistic dataset of 8 sharp, natural images. They apply inverse gamma curve, synthetically blur the images and finally, they saturate the pixels by clipping them at the 98th percentile. They also add Gaussian noise and quantization. In this way, they generate degraded images applying all three degradations that the model can tackle. The results are shown in the figure.
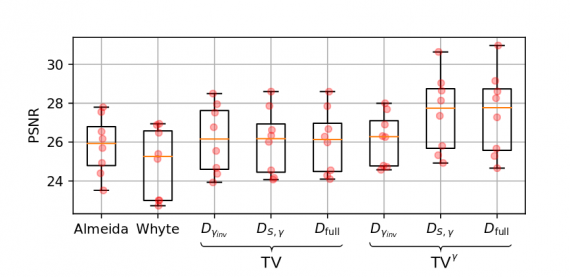
This method shows that previous approaches to de-blurring are over-simplistic. Moreover, it shows that the image formation pipeline is a complex non-linear mapping and de-blurring is not a trivial task. However, addressing the common, known image degradations using energy minimization algorithm and well-defined functions gives excellent results despite the complexity of the problem. Anyway, this approach works with non-blind deconvolution, and the authors leave the extension of the method to blind deconvolution as future work.