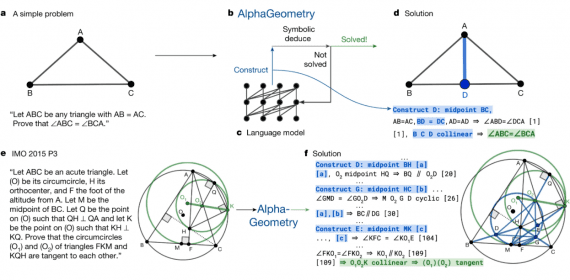
Large language models perform well on mathematical benchmarks like AIME, however International Mathematical Olympiad (IMO) problems require deep understanding, creativity, and formal reasoning. Chinese researchers used Google Gemini 2.5 Pro on recently published IMO 2025 problems, avoiding data contamination. By applying a self-verification pipeline with careful prompt design, they correctly solved 5 out of 6 problems. This result underscores the importance of developing optimal strategies to harness the full potential of powerful LLMs for complex reasoning tasks.
Strategy and Solution Methodology
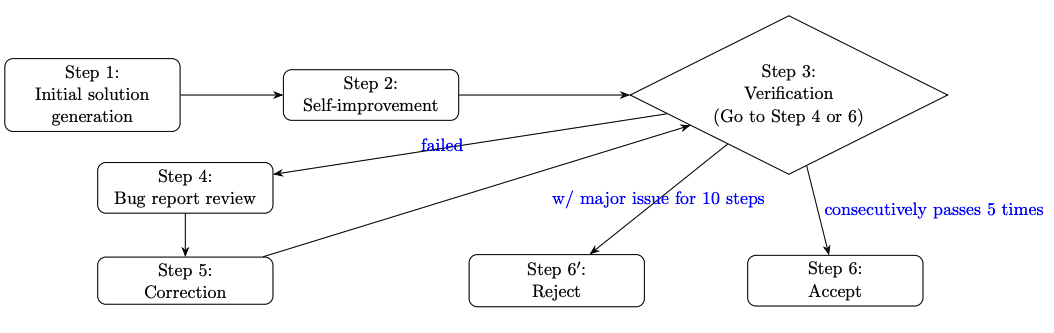
The researchers developed a multi-stage pipeline for solving olympiad-level problems:
Self-verification pipeline includes the following stages:
- Initial solution generation with emphasis on rigor;
- Model self-improvement;
- Solution verification and bug report generation;
- Bug report analysis;
- Solution correction and improvement;
- Solution acceptance or rejection.
Key prompting principles:
- Rigor above all — every step must be logically justified;
- Honesty about completeness — better to present partial but rigorous results;
- Use of TeX formatting for all mathematical expressions;
- Structured response format with summary and detailed solution.
Role of the Verifier
The verifier plays a critical role in the pipeline, classifying issues into: critical errors — those that break the logical chain of proof (logical fallacies, factual inaccuracies) and justification gaps — steps where the conclusion may be correct, but the argumentation is incomplete or insufficiently rigorous.
The system runs the verifier five times at the final stage and accepts a solution only upon successful passage of all checks.
Analysis of IMO 2025 Problem Solutions by Gemini 2.5 Pro
Problem 1 (Combinatorial Geometry)
The problem required determining all non-negative integers k for line configurations in the plane. Gemini 2.5 Pro successfully applied mathematical induction, reducing the problem to a base case and showing that the possible values are k ∈ {0, 1, 3}.
The key insight was that any configuration can be reduced to a case where none of the lines is a “principal boundary line” of the point set. Through careful analysis of intersection constraints and using properties of “sunny” lines (not parallel to the x-axis, y-axis, and line x+y=0), the model proved the impossibility of configurations with k=2 or k≥4, while constructing explicit examples for admissible cases.
Problem 2 (Analytic Geometry)
The geometric tangency problem was solved using analytic geometry methods. The model established a coordinate system and used algebraic calculations to prove the tangency condition.
The complexity of the problem lay in the need to coordinate the mutual arrangement of two circles, their centers, intersection points, and the orthocenter of a triangle. Gemini 2.5 Pro methodically calculated coordinates of all key points, including the circumcenter of triangle ACD and the orthocenter of triangle PMN, then used the tangency condition through equality of the squared distance from circle center to line with the squared radius to complete the proof.
Problem 3 (Number Theory)
The functional equation required finding the minimal constant c. The investigation showed that f(1) = 1, analyzed possible structures for the set of prime numbers, and determined c = 4.
The most technically complex part of the solution involved analyzing the set of primes Sf = {p prime | ∃n ∈ N, p | f(n)} and proving that only three cases are possible: Sf = ∅, Sf = {2}, or Sf contains all primes. Through deep analysis of modular comparisons and application of Dirichlet’s theorem on primes in arithmetic progressions, the model excluded most intermediate cases and constructed a maximal function f₀(n) achieving the bound c = 4.
Problem 4 (Sequences)
Analysis of a recurrent sequence with constraints on proper divisors. The solution established that all elements must be even and divisible by 3, but not by 5, leading to complete characterization of possible initial values.
The elegance of the solution manifested in systematic proof of necessary divisibility conditions through analysis of the recurrence relation an+1 = f(an), where f(N) is the sum of the three largest proper divisors. The model showed that if the sequence contains an odd element, it becomes strictly decreasing and terminates, similarly for elements not divisible by 3. The constructive part of the proof included building explicit examples of infinite sequences for each admissible type of initial values.
Problem 5 (Game Theory)
A game between Alice and Bazza with different constraints. Analysis showed that the outcome depends on parameter λ: for λ > √2/2 Alice wins, for λ < √2/2 Bazza wins, for λ = √2/2 it’s a draw. The solution required deep analysis of optimal strategies for both sides. For the case λ > √2/2, the model developed a winning strategy for Alice, based on choosing a sufficiently large m and playing zeros until move 2m-1, then choosing a value making Bazza’s next move impossible. A key element was proving that the maximum value of Bazza’s defensive function equals m√2, which allowed establishing the exact winning condition. The critical case λ = √2/2 required proving that neither player has a winning strategy.
Problem 6 (Combinatorial Optimization)
The model reported only the trivial upper bound 4048 for the problem about minimum number of tiles.
This problem proved most challenging for the model, as it required complex combinatorial optimization of placing rectangular tiles on a 2025×2025 grid such that each row and column has exactly one uncovered square. The trivial upper bound 4048 comes from the approach of placing one tile in each row and column, but the optimal solution is probably significantly smaller. The model’s inability to find a tighter bound indicates limitations of current LLMs in high-dimensional discrete optimization problems.
Overcoming Limitations
Computational budget constraints: Gemini 2.5 Pro’s maximum thinking token count is 32768, which is insufficient for completely solving a typical IMO problem. Breaking the process into stages allows efficient use of additional budgets for continued reasoning.
Avoiding data contamination: using actual IMO 2025 problems ensures clean testing of the model’s capabilities without data leakage.
Significance of Results
The research demonstrated that powerful existing models are already capable of solving complex mathematical reasoning problems, but direct use can lead to poor results. The developed approach shows significant progress in mathematical reasoning for LLMs.
The results indicate that with proper methodology, modern LLMs can achieve levels comparable to mathematical olympiad medalists, opening new possibilities for AI application in mathematical research and education.RetryClaude can make mistakes. Please double-check responses.