Метод обратного распространения ошибки: математика, примеры, код

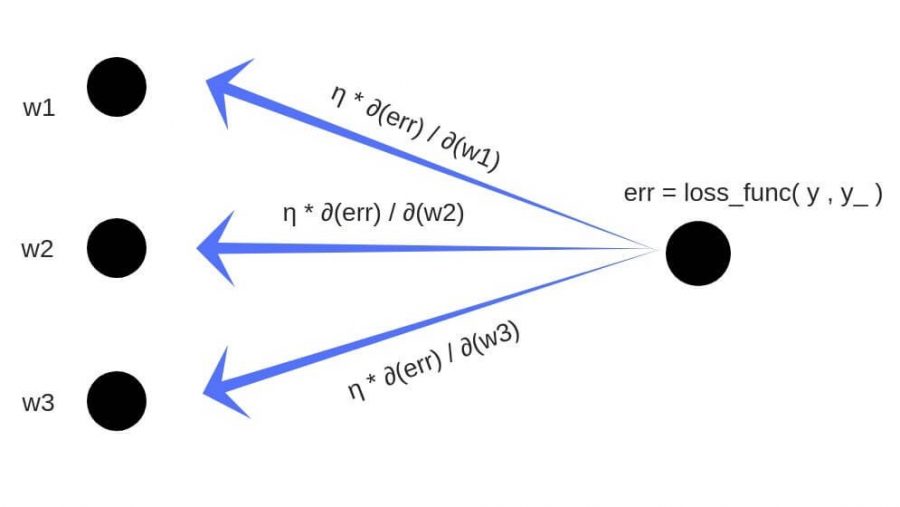
Обратное распространение ошибки — это способ обучения нейронной сети. Цели обратного распространения просты: отрегулировать каждый вес пропорционально тому, насколько он способствует общей ошибке. Если мы будем итеративно уменьшать ошибку каждого веса, в конце концов у нас будет ряд весов, которые дают хорошие прогнозы.

Обновление правила цепочки

Прямое распространение можно рассматривать как длинный ряд вложенных уравнений. Если вы так думаете о прямом распространении, то обратное распространение — это просто приложение правила цепочки (дифференцирования сложной функции) для поиска производных потерь по любой переменной во вложенном уравнении. С учётом функции прямого распространения:

f(x)=A(B(C(x)))

A, B, и C — функции активации на различных слоях. Пользуясь правилом цепочки, мы легко вычисляем производную f(x) по x:

f′(x)=f′(A)⋅A′(B)⋅B′(C)⋅C′(x)

Что насчёт производной относительно B? Чтобы найти производную по B, вы можете сделать вид, что B (C(x)) является константой, заменить ее переменной-заполнителем B, и продолжить поиск производной по B стандартно.

f′(B)=f′(A)⋅A′(B)

Этот простой метод распространяется на любую переменную внутри функции, и позволяет нам в точности определить влияние каждой переменной на общий результат.

Применение правила цепочки

Давайте используем правило цепочки для вычисления производной потерь по любому весу в сети. Правило цепочки поможет нам определить, какой вклад каждый вес вносит в нашу общую ошибку и направление обновления каждого веса, чтобы уменьшить ошибку. Вот уравнения, которые нужны, чтобы сделать прогноз и рассчитать общую ошибку или потерю:

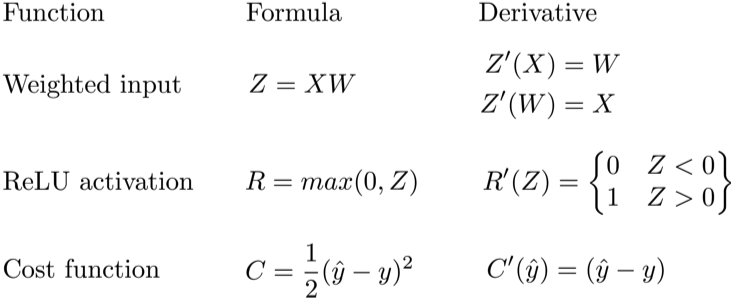
Учитывая сеть, состоящую из одного нейрона, общая потеря нейросети может быть рассчитана как:

Cost=C(R(Z(XW)))

Используя правило цепочки, мы легко можем найти производную потери относительно веса W.

C′(W)=C′(R)⋅R′(Z)⋅Z′(W)=(y^−y)⋅R′(Z)⋅X

Теперь, когда у нас есть уравнение для вычисления производной потери по любому весу, давайте обратимся к примеру с нейронной сетью:

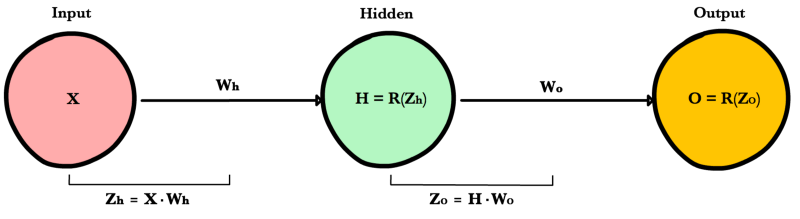
Какова производная от потери по Wo?

C′(WO)=C′(y^)⋅y^′(ZO)⋅Z′O(WO)=(y^−y)⋅R′(ZO)⋅H

А что насчет Wh? Чтобы узнать это, мы просто продолжаем возвращаться в нашу функцию, рекурсивно применяя правило цепочки, пока не доберемся до функции, которая имеет элемент Wh.

C′(Wh)=C′(y^)⋅O′(Zo)⋅Z′o(H)⋅H′(Zh)⋅Z′h(Wh)=(y^−y)⋅R′(Zo)⋅Wo⋅R′(Zh)⋅X

И просто забавы ради, что, если в нашей сети было бы 10 скрытых слоев. Что такое производная потери для первого веса w1?

C(w1)=(dC/dy^)⋅(dy^/dZ11)⋅(dZ11/dH10)⋅(dH10/dZ10)⋅(dZ10/dH9)⋅(dH9/dZ9)⋅(dZ9/dH8)⋅(dH8/dZ8)⋅(dZ8/dH7)⋅(dH7/dZ7)⋅(dZ7/dH6)⋅(dH6/dZ6)⋅(dZ6/dH5)⋅(dH5/dZ5)⋅(dZ5/dH4)⋅(dH4/dZ4)⋅(dZ4/dH3)⋅(dH3/dZ3)⋅(dZ3/dH2)⋅(dH2/dZ2)⋅(dZ2/dH1)⋅(dH1/dZ1)⋅(dZ1/dW1)

Заметили закономерность? Количество вычислений, необходимых для расчёта производных потерь, увеличивается по мере углубления нашей сети. Также обратите внимание на избыточность в наших расчетах производных. Производная потерь каждого слоя добавляет два новых элемента к элементам, которые уже были вычислены слоями над ним. Что, если бы был какой-то способ сохранить нашу работу и избежать этих повторяющихся вычислений?

Сохранение работы с мемоизацией

Мемоизация — это термин в информатике, имеющий простое значение: не пересчитывать одно и то же снова и снова. В мемоизации мы сохраняем ранее вычисленные результаты, чтобы избежать пересчета одной и той же функции. Это удобно для ускорения рекурсивных функций, одной из которых является обратное распространение. Обратите внимание на закономерность в уравнениях производных приведённых ниже.

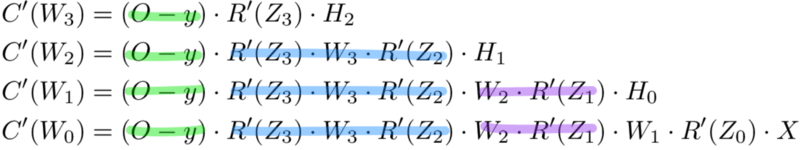
Каждый из этих слоев пересчитывает одни и те же производные! Вместо того, чтобы выписывать длинные уравнения производных для каждого веса, можно использовать мемоизацию, чтобы сохранить нашу работу, так как мы возвращаем ошибку через сеть. Для этого мы определяем 3 уравнения (ниже), которые вместе выражают в краткой форме все вычисления, необходимые для обратного распространения. Математика та же, но уравнения дают хорошее сокращение, которое мы можем использовать, чтобы отслеживать те вычисления, которые мы уже выполнили, и сохранять нашу работу по мере продвижения назад по сети.

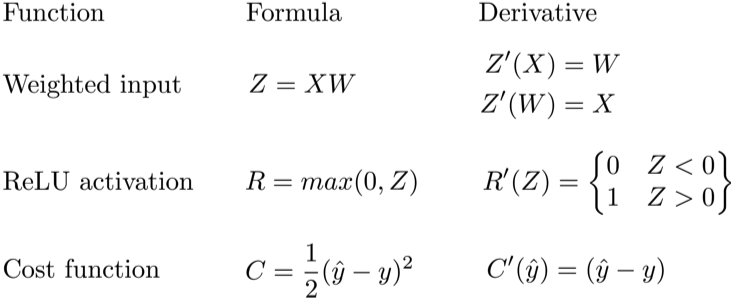
Для начала мы вычисляем ошибку выходного слоя и передаем результат на скрытый слой перед ним. После вычисления ошибки скрытого слоя мы передаем ее значение обратно на предыдущий скрытый слой. И так далее и тому подобное. Возвращаясь назад по сети, мы применяем 3-ю формулу на каждом слое, чтобы вычислить производную потерь по весам этого слоя. Эта производная говорит нам, в каком направлении регулировать наши веса, чтобы уменьшить общие потери.

Примечание: термин ошибка слоя относится к производной потерь по входу в слой. Он отвечает на вопрос: как изменяется выход функции потерь при изменении входа в этот слой?

Ошибка выходного слоя

Для расчета ошибки выходного слоя необходимо найти производную потерь по входу выходному слою, Zo. Это отвечает на вопрос: как веса последнего слоя влияют на общую ошибку в сети?  Тогда производная такова:

C′(Zo)=(y^−y)⋅R′(Zo)

Чтобы упростить запись, практикующие МО обычно заменяют последовательность (y^−y)∗R'(Zo) термином Eo. Итак, наша формула для ошибки выходного слоя равна:

Eo=(y^−y)⋅R′(Zo)

Ошибка скрытого слоя

Для вычисления ошибки скрытого слоя нужно найти производную потерь по входу скрытого слоя, Zh.

C′(Zh)=(y^−y)⋅R′(Zo)⋅Wo⋅R′(Zh)

Далее мы можем поменять местами элемент Eo выше, чтобы избежать дублирования и создать новое упрощенное уравнение для ошибки скрытого слоя:

Eh=Eo⋅Wo⋅R′(Zh)

Эта формула лежит в основе обратного распространения. Мы вычисляем ошибку текущего слоя и передаем взвешенную ошибку обратно на предыдущий слой, продолжая процесс, пока не достигнем нашего первого скрытого слоя. Попутно мы обновляем веса, используя производную потерь по каждому весу.

Производная потерь по любому весу

Вернемся к нашей формуле для производной потерь по весу выходного слоя Wo.

C′(WO)=(y^−y)⋅R′(ZO)⋅H

Мы знаем, что можем заменить первую часть уравнением для ошибки выходного слоя Eh. H представляет собой активацию скрытого слоя.

C′(Wo)=Eo⋅H

Таким образом, чтобы найти производную потерь по любому весу в нашей сети, мы просто умножаем ошибку соответствующего слоя на его вход (выход предыдущего слоя).

C′(w)=CurrentLayerError⋅CurrentLayerInput

Примечание: вход относится к активации с предыдущего слоя, а не к взвешенному входу, Z.

Подводя итог

Вот последние 3 уравнения, которые вместе образуют основу обратного распространения.

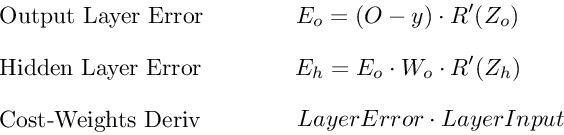
Вот процесс, визуализированный с использованием нашего примера нейронной сети выше:

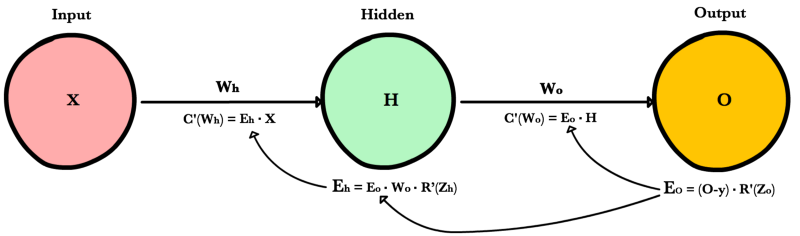
Обратное распространение: пример кода

def relu_prime(z):
if z > 0:
return 1
return 0

def cost(yHat, y):
return 0.5 * (yHat - y)**2

def cost_prime(yHat, y):
return yHat - y

def backprop(x, y, Wh, Wo, lr):
yHat = feed_forward(x, Wh, Wo)

# Layer Error
Eo = (yHat - y) * relu_prime(Zo)
Eh = Eo * Wo * relu_prime(Zh)

# Cost derivative for weights
dWo = Eo * H
dWh = Eh * x

# Update weights
Wh -= lr * dWh
Wo -= lr * dWo

Генерируйте видео, изображения и аватары с помощью сервиса FabulaAI. Получите 10 бесплатных генераций сразу после регистрации!