Как работает нейронная сеть: алгоритмы, обучение, виды нейросетей

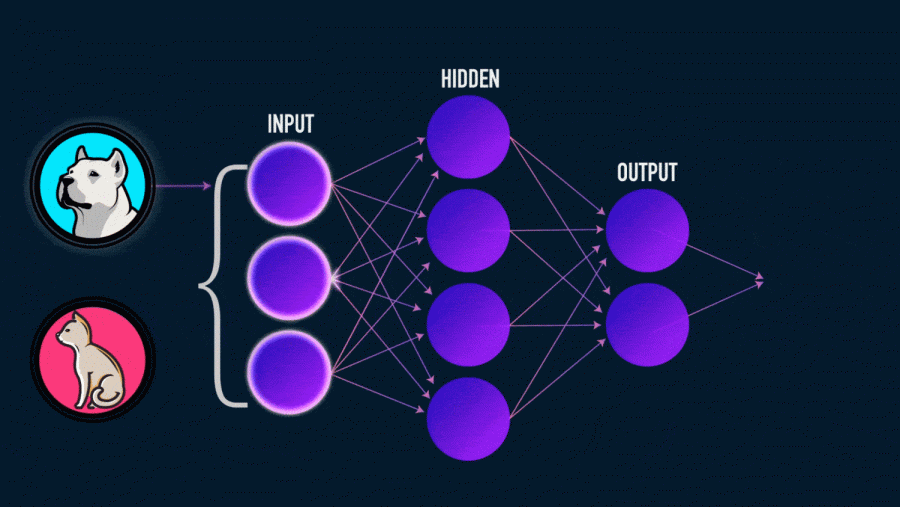
Нейронная сеть — попытка с помощью математических моделей воспроизвести работу человеческого мозга для создания машин, обладающих искусственным интеллектом.

Нейросеть обычно обучается с учителем. Это означает наличие обучающего набора данных (датасета), который содержит примеры с правильными результатами решений: ответами на вопросы, метками, сегментами, классами. Нейронная сеть пытается воспроизвести результат самостоятельно на новом наборе данных.

Неразмеченные наборы также используют для обучения нейронных сетей, но мы не будем здесь это рассматривать.

Например, если вы хотите создать нейросеть для оценки эмоциональную тональности текста, датасетом будет список предложений с соответствующими каждому эмоциональными оценками. Тональность текста определяют признаки (слова, фразы, структура предложения), которые придают негативную или позитивную окраску. Веса признаков в итоговой оценке тональности текста (позитивный, негативный, нейтральный) зависят от математической функции, которая вычисляется во время обучения нейронной сети.

Раньше люди генерировали признаки вручную. Чем больше признаков и точнее подобраны веса, тем точнее ответ. Нейронная сеть автоматизировала этот процесс.

Из чего состоит нейронная сеть

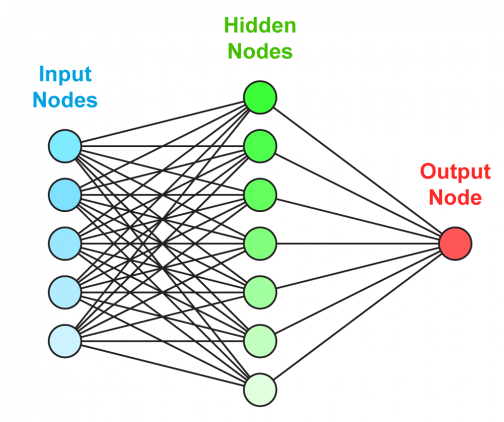
Искусственная нейронная сеть состоит из трех компонентов:

• • Входной слой;
  • Скрытые (вычислительные) слои;
  • Выходной слой.

Обучение нейросети происходит в два этапа:

1. Прямое распространение ошибки;
2. Обратное распространение ошибки.

Во время прямого распространения ошибки делается предсказание ответа. При обратном распространении ошибка между фактическим ответом и предсказанным минимизируется.

Визуализация работы нейронной сети для классификации изображений:

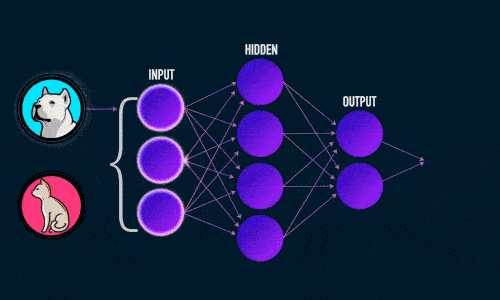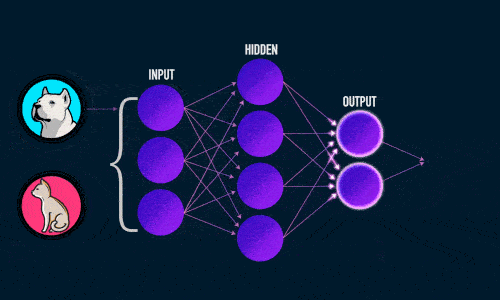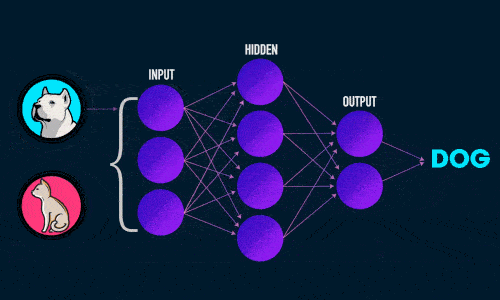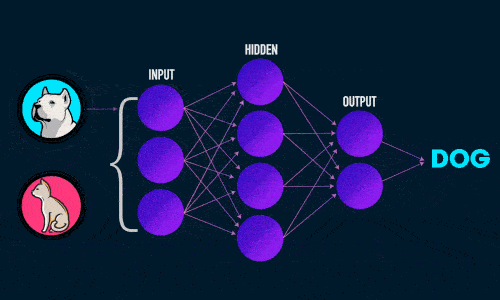
Обучение: прямое распространение ошибки

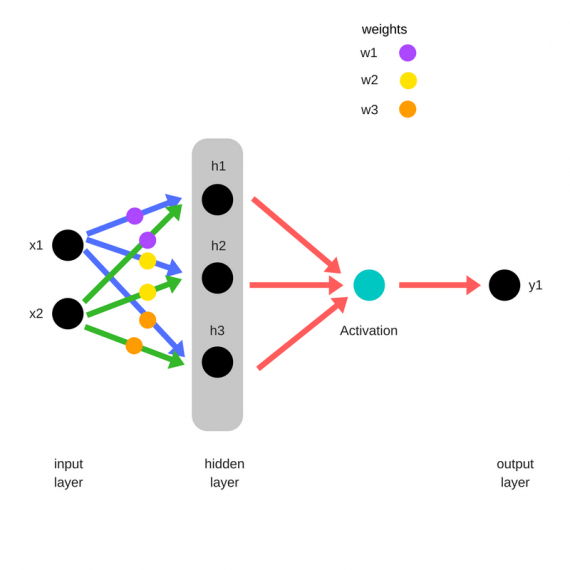
Зададим начальные веса случайным образом:

• w1
• w2
• w3

Умножим входные данные на веса для формирования скрытого слоя:

• h1 = (x1 * w1) + (x2 * w1)
• h2 = (x1 * w2) + (x2 * w2)
• h3 = (x1 * w3) + (x2 * w3)

Выходные данные из скрытого слоя передается через нелинейную функцию (функцию активации), для получения выхода сети:

• y_ = fn(h1 , h2, h3)

Обратное распространение

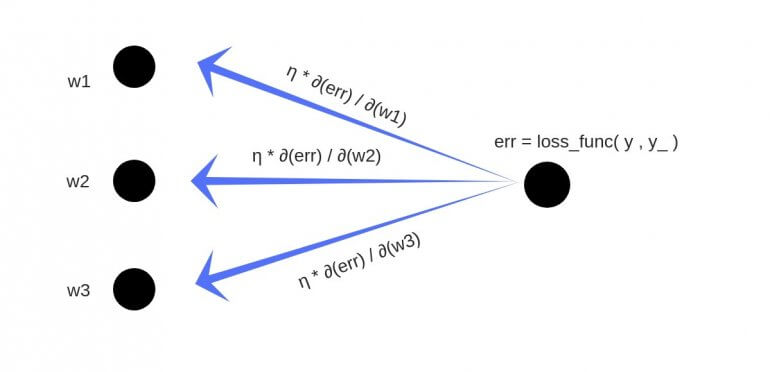
• Суммарная ошибка (total_error) вычисляется как разность между ожидаемым значением «y» (из обучающего набора) и полученным значением «y_» (посчитанное на этапе прямого распространения ошибки), проходящих через функцию потерь (cost function).
• Частная производная ошибки вычисляется по каждому весу (эти частные дифференциалы отражают вклад каждого веса в общую ошибку (total_loss)).
• Затем эти дифференциалы умножаются на число, называемое скорость обучения или learning rate (η).

Полученный результат затем вычитается из соответствующих весов.

В результате получатся следующие обновленные веса:

• w1 = w1 — (η * ∂(err) / ∂(w1))
• w2 = w2 — (η * ∂(err) / ∂(w2))
• w3 = w3 — (η * ∂(err) / ∂(w3))

То, что мы предполагаем и инициализируем веса случайным образом, и они будут давать точные ответы, звучит не вполне обоснованно, тем не менее, работает хорошо.

Если вы знакомы с рядами Тейлора, обратное распространение ошибки имеет такой же конечный результат. Только вместо бесконечного ряда мы пытаемся оптимизировать только его первый член.

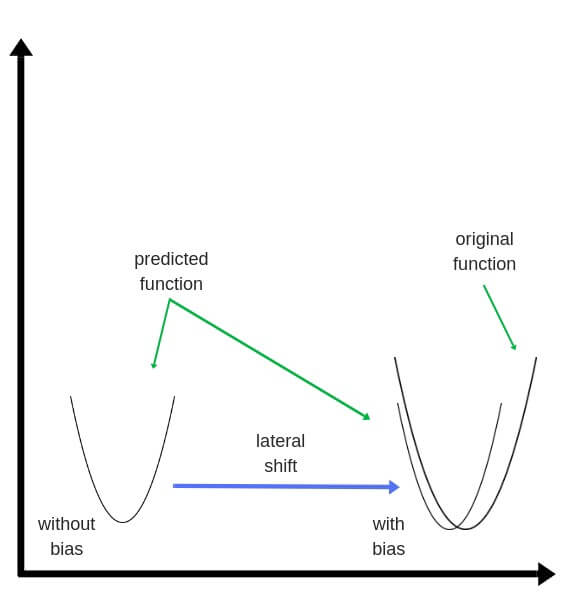
Смещения – это веса, добавленные к скрытым слоям. Они тоже случайным образом инициализируются и обновляются так же, как скрытый слой. Роль скрытого слоя заключается в том, чтобы определить форму базовой функции в данных, в то время как роль смещения – сдвинуть найденную функцию в сторону так, чтобы она частично совпала с исходной функцией.

Частные производные

Частные производные можно вычислить, поэтому известно, какой был вклад в ошибку по каждому весу. Необходимость производных очевидна. Представьте нейронную сеть, пытающуюся найти оптимальную скорость беспилотного автомобиля. Eсли машина обнаружит, что она едет быстрее или медленнее требуемой скорости, нейронная сеть будет менять скорость, ускоряя или замедляя автомобиль. Что при этом ускоряется/замедляется? Производные скорости.

Разберем необходимость частных производных на примере.

Предположим, детей попросили бросить дротик в мишень, целясь в центр. Вот результаты:

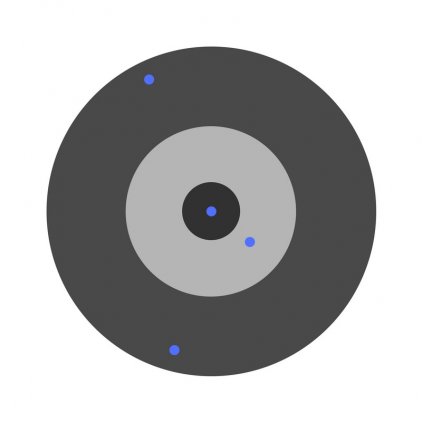
Теперь, если мы найдем общую ошибку и просто вычтем ее из всех весов, мы обобщим ошибки, допущенные каждым. Итак, скажем, ребенок попал слишком низко, но мы просим всех детей стремиться попадать в цель, тогда это приведет к следующей картине:

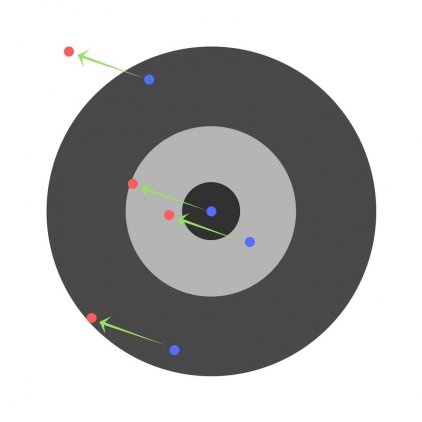
Ошибка нескольких детей может уменьшиться, но общая ошибка все еще увеличивается.

Найдя частные производные, мы узнаем ошибки, соответствующие каждому весу в отдельности. Если выборочно исправить веса, можно получить следующее:

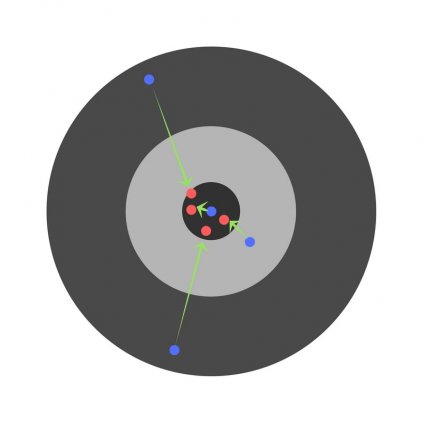
Гиперпараметры нейронной сети

Нейронная сеть используется для автоматизации отбора признаков, но некоторые параметры настраиваются вручную.

Скорость обучения (learning rate) нейросети

Скорость обучения является очень важным гиперпараметром. Если скорость обучения слишком мала, то даже после обучения нейронной сети в течение длительного времени она будет далека от оптимальных результатов. Результаты будут выглядеть примерно так:

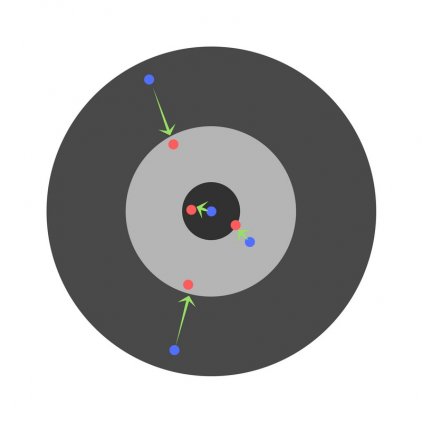
С другой стороны, если скорость обучения слишком высока, то сеть очень быстро выдаст ответы. Получится следующее:

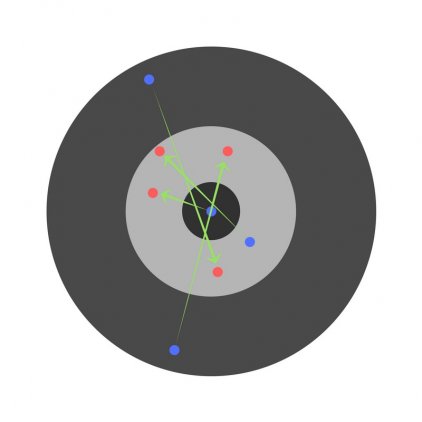
Функция активации (activation function) нейронной сети

Функция активации — это один из самых мощных инструментов, который влияет на силу, приписываемую нейронным сетям. Отчасти, она определяет, какие нейроны будут активированы, другими словами и какая информация будет передаваться последующим слоям.

Без функций активации глубокие сети теряют значительную часть своей способности к обучению. Нелинейность этих функций отвечает за повышение степени свободы, что позволяет обобщать проблемы высокой размерности в более низких измерениях. Ниже приведены примеры распространенных функций активации:

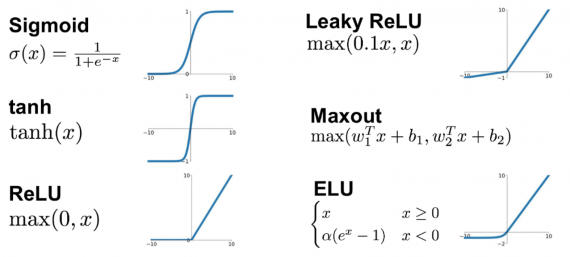
Функция потери (loss function)

Функция потерь находится в центре нейронной сети. Она используется для расчета ошибки между  реальными и полученными ответами. Наша глобальная цель — минимизировать эту ошибку. Таким образом, функция потерь эффективно приближает обучение нейронной сети к этой цели.

Функция потерь измеряет «насколько хороша» нейронная сеть в отношении данной обучающей выборки и ожидаемых ответов. Она также может зависеть от таких переменных, как веса и смещения.

Функция потерь одномерна и не является вектором, поскольку она оценивает, насколько хорошо нейронная сеть работает в целом.

Некоторые известные функции потерь:

• Квадратичная (среднеквадратичное отклонение);
• Кросс-энтропия;
• Экспоненциальная (AdaBoost);
• Расстояние Кульбака-Лейблера или прирост информации.

Cреднеквадратичное отклонение – самая простая функция потерь и наиболее часто используемая. Она задается следующим образом:

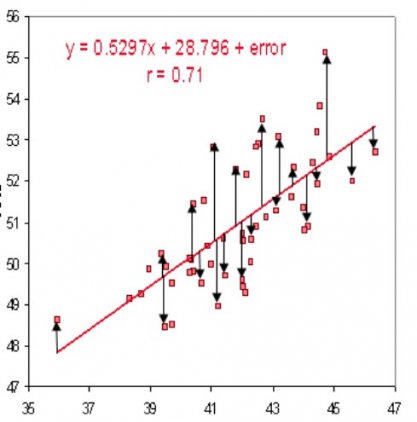
Функция потерь в нейронной сети должна удовлетворять двум условиям:

• Функция потерь должна быть записана как среднее;
• Функция потерь не должна зависеть от каких-либо активационных значений нейронной сети, кроме значений, выдаваемых на выходе.

Глубокая нейронная сеть

Глубокое обучение (deep learning) – это класс алгоритмов машинного обучения, которые учатся глубже (более абстрактно) понимать данные. Популярные алгоритмы нейронных сетей глубокого обучения представлены на схеме ниже.

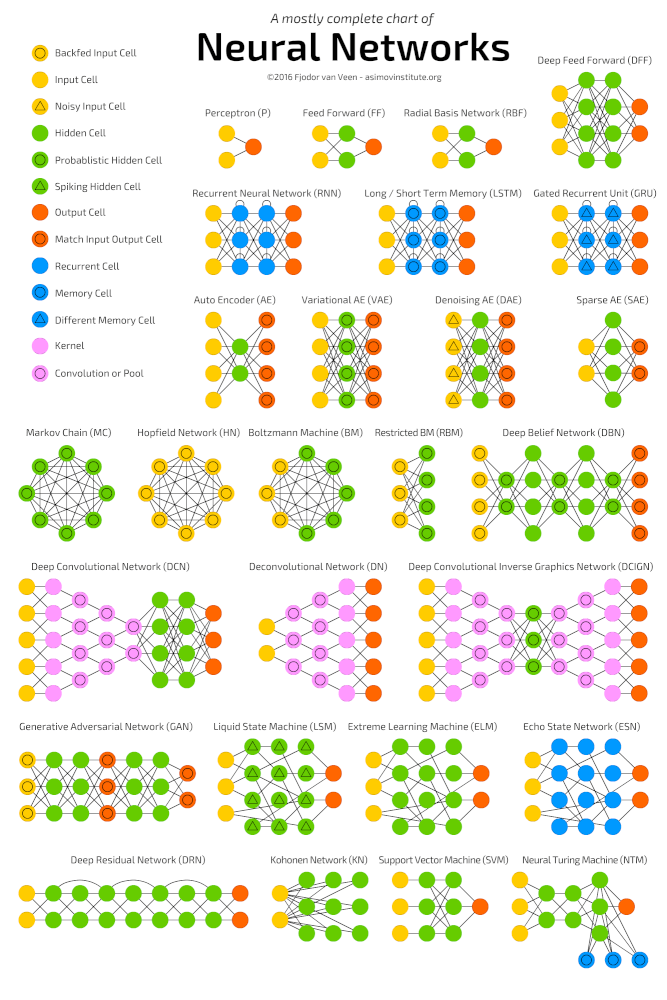
Более формально в deep learning:

• Используется каскад (пайплайн, как последовательно передаваемый поток) из множества обрабатывающих слоев (нелинейных) для извлечения и преобразования признаков;
• Основывается на изучении признаков (представлении информации) в данных без обучения с учителем. Функции более высокого уровня (которые находятся в последних слоях) получаются из функций нижнего уровня (которые находятся в слоях начальных слоях);
• Изучает многоуровневые представления, которые соответствуют разным уровням абстракции; уровни образуют иерархию представления.

Пример простой нейронной сети

Рассмотрим однослойную нейронную сеть:

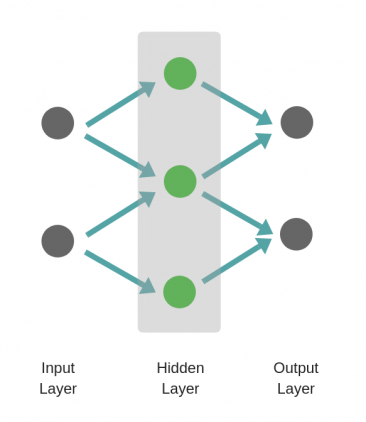
Здесь, обучается первый слой (зеленые нейроны), он просто передается на выход.

В то время как в случае двухслойной нейронной сети, независимо от того, как обучается зеленый скрытый слой, он затем передается на синий скрытый слой, где продолжает обучаться:

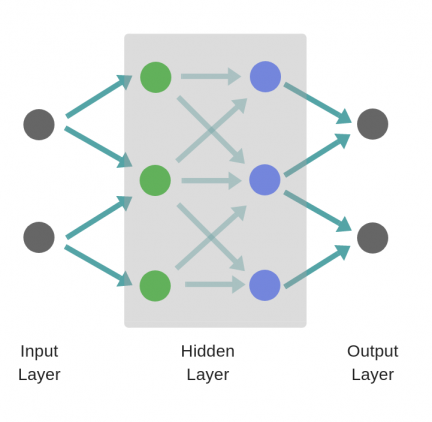
Следовательно, чем больше число скрытых слоев, тем больше возможности обучения сети.

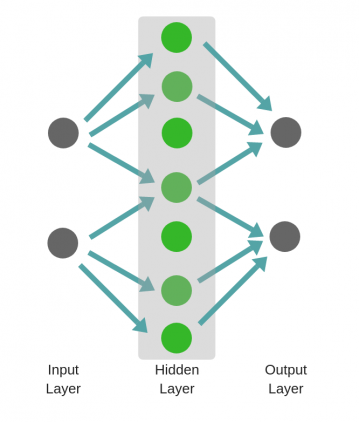
Не следует путать с широкой нейронной сетью.

В этом случае большое число нейронов в одном слое не приводит к глубокому пониманию данных. Но это приводит к изучению большего числа признаков.

Пример:

Изучая английскую грамматику, требуется знать огромное число понятий. В этом случае однослойная широкая нейронная сеть работает намного лучше, чем глубокая нейронная сеть, которая значительно меньше.

Но

В случае изучения преобразования Фурье, ученик (нейронная сеть) должен быть глубоким, потому что не так много понятий, которые нужно знать, но каждое из них достаточно сложное и требует глубокого понимания.

Главное — баланс

Очень заманчиво использовать глубокие и широкие нейронные сети для каждой задачи. Но это может быть плохой идеей, потому что:

• Обе требуют значительно большего количества данных для обучения, чтобы достичь минимальной желаемой точности;
• Обе имеют экспоненциальную сложность;
• Слишком глубокая нейронная сеть попытается сломать фундаментальные представления, но при этом она будет делать ошибочные предположения и пытаться найти псевдо-зависимости, которые не существуют;
• Слишком широкая нейронная сеть будет пытаться найти больше признаков, чем есть. Таким образом, подобно предыдущей, она начнет делать неправильные предположения о данных.

Проклятье размерности нейросети

Проклятие размерности относится к различным явлениям, возникающим при анализе и организации данных в многомерных пространствах (часто с сотнями или тысячами измерений), и не встречается в ситуациях с низкой размерностью.

Грамматика английского языка имеет огромное количество аттрибутов, влияющих на нее. В машинном обучении мы должны представить их признаками в виде массива/матрицы конечной и существенно меньшей длины (чем количество существующих признаков). Для этого сети обобщают эти признаки. Это порождает две проблемы:

• Из-за неправильных предположений появляется смещение. Высокое смещение может привести к тому, что алгоритм пропустит существенную взаимосвязь между признаками и целевыми переменными. Это явление называют недообучение.
• От небольших отклонений в обучающем множестве из-за недостаточного изучения признаков увеличивается дисперсия. Высокая дисперсия ведет к переобучению, ошибки воспринимаются в качестве надежной информации.

Компромисс

На ранней стадии обучения смещение велико, потому что выход из сети далек от желаемого. А дисперсия очень мала, поскольку данные имеет пока малое влияние.

В конце обучения смещение невелико, потому что сеть выявила основную функцию в данных. Однако, если обучение слишком продолжительное, сеть также изучит шум, характерный для этого набора данных. Это приводит к большому разбросу результатов при тестировании на разных множествах, поскольку шум меняется от одного набора данных к другому.

Действительно,

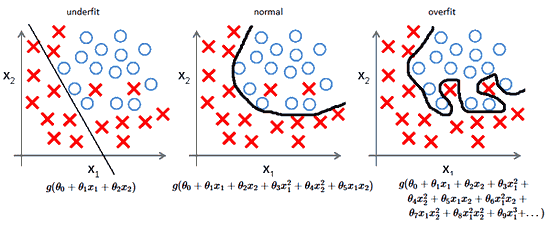
алгоритмы с большим смещением обычно в основе более простых моделей, которые не склонны к переобучению, но могут недообучиться и не выявить важные закономерности или свойства признаков. Модели с маленьким смещением и большой дисперсией обычно более сложны с точки зрения их структуры, что позволяет им более точно представлять обучающий набор. Однако они могут отображать много шума из обучающего набора, что делает их прогнозы менее точными, несмотря на их дополнительную сложность.

Как правило, невозможно иметь маленькое смещение и маленькую дисперсию одновременно.

Есть множество инструментов, с помощью которых можно легко создать сложные модели машинного обучения, переобучение занимает центральное место. Поскольку смещение появляется, когда сеть не получает достаточно информации. Но чем больше примеров, тем больше появляется вариантов зависимостей и изменчивостей в этих корреляциях.