Функции активации нейросети: сигмоида, линейная, ступенчатая, ReLu, tahn

Что делает искусственный нейрон? Простыми словами, он считает взвешенную сумму на своих входах, добавляет смещение (bias) и решает, следует это значение исключать или использовать дальше (да, функция активации так и работает, но давайте пойдем по порядку). 

Функция активации определяет выходное значение нейрона в зависимости от результата взвешенной суммы входов и порогового значения.

Рассмотрим нейрон:

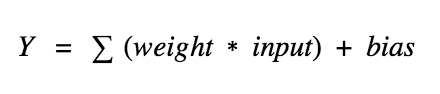
Теперь значение Y может быть любым в диапазоне от -бесконечности до +бесконечности. В действительности нейрон не знает границу, после которой следует активация. Ответим на вопрос, как мы решаем, должен ли нейрон быть активирован (мы рассматриваем паттерн активации, так как можем провести аналогию с биологией. Именно таким образом работает мозг, а мозг — хорошее свидетельство работы сложной и разумной системе).

Для этой цели решили добавлять активационную функцию. Она проверяет произведенное нейроном значение Y на предмет того, должны ли внешние связи рассматривать этот нейрон как активированный, или его можно игнорировать.

Ступенчатая функция активации

Первое, что приходит в голову, это вопрос о том, что считать границей активации для активационной функции. Если значение Y больше некоторого порогового значения, считаем нейрон активированным. В противном случае говорим, что нейрон неактивен. Такая схема должна сработать, но сначала давайте её формализуем.

• Функция А = активирована, если Y > граница, иначе нет.
• Другой способ:  A = 1, если Y > граница, иначе А = 0.

Функция, которую мы только что создали, называется ступенчатой. Такая функция представлена на рисунке ниже.

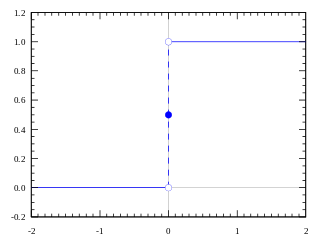
Функция принимает значение 1 (активирована), когда Y > 0 (граница), и значение 0 (не активирована) в противном случае.

Мы создали активационную функцию для нейрона. Это простой способ, однако в нём есть недостатки. Рассмотрим следующую ситуацию.

Представим, что мы создаем бинарный классификатор — модель, которая должна говорить “да” или “нет” (активирован или нет). Ступенчатая функция сделает это за вас — она в точности выводит 1 или 0.

Теперь представим случай, когда требуется большее количество нейронов для классификации многих классов: класс1, класс2, класс3 и так далее. Что будет, если активированными окажутся больше чем 1 нейрон? Все нейроны из функции активации выведут 1. В таком случае появляются вопросы о том, какой класс должен в итоге получиться для заданного объекта.

Мы хотим, чтобы активировался только один нейрон, а функции активации других нейронов были равна нулю (только в этом случае можно быть уверенным, что сеть правильно определяет класс). Такую сеть труднее обучать и добиваться сходимости. Если активационная функция не бинарная, то возможны значения “активирован на 50%”, “активирован на 20%” и так далее. Если активированы несколько нейронов, можно найти нейрон с наибольшим значением активационной функции (лучше, конечно, чтобы это была softmax функция, а не max. Но пока не будем заниматься этими вопросами).

Но в таком случае, как и ранее, если более одного нейрона говорят “активирован на 100%”, проблема по прежнему остается. Так как существуют промежуточные значения на выходе нейрона, процесс обучения проходит более гладко и быстро, а вероятность появления нескольких полностью активированных нейронов во время тренировки снижается по сравнению со ступенчатой функцией активации (хотя это зависит от того, что вы обучаете и на каких данных).

Мы определились, что хотим получать промежуточные значения активационной функции (аналоговая функция), а не просто говорить “активирован” или нет (бинарная функция).

Первое, что приходит в голову — линейная функция.

Линейная функция активации

A = cx

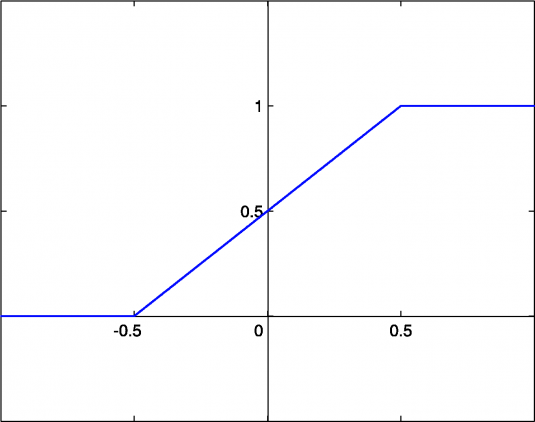
Линейная функция представляет собой прямую линию и пропорциональна входу (то есть взвешенной сумме на этом нейроне).

Такой выбор активационной функции позволяет получать спектр значений, а не только бинарный ответ. Можно соединить несколько нейронов вместе и, если более одного нейрона активировано, решение принимается на основе применения операции max (или softmax). Но и здесь не без проблем.

Если вы знакомы с методом градиентного спуска для обучения, то можете заметить, что для этой функции производная равна постоянной.

Производная от A=cx по x равна с. Это означает, что градиент никак не связан с Х. Градиент является постоянным вектором, а спуск производится по постоянному градиенту. Если производится ошибочное предсказание, то изменения, сделанные обратным распространением ошибки, тоже постоянны и не зависят от изменения на входе delta(x).

Это не есть хорошо (не всегда, но в большинстве случаев). Но существует и другая проблема. Рассмотрим связанные слои. Каждый слой активируется линейной функцией. Значение с этой функции идет в следующий слой в качестве входа, второй слой считает взвешенную сумму на своих входах и, в свою очередь, включает нейроны в зависимости от другой линейной активационной функции.

Не имеет значения, сколько слоев мы имеем. Если все они по своей природе линейные, то финальная функция активации в последнем слое будет просто линейной функцией от входов на первом слое! Остановитесь на мгновение и обдумайте эту мысль.

Это означает, что два слоя (или N слоев) могут быть заменены одним слоем. Мы потеряли возможность делать наборы из слоев. Не важно, как мы стэкаем, вся нейронная сеть все равно будет подобна одному слою с линейной функцией активации (комбинация линейных функций линейным образом — другая линейная функция).

Сигмоида

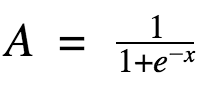
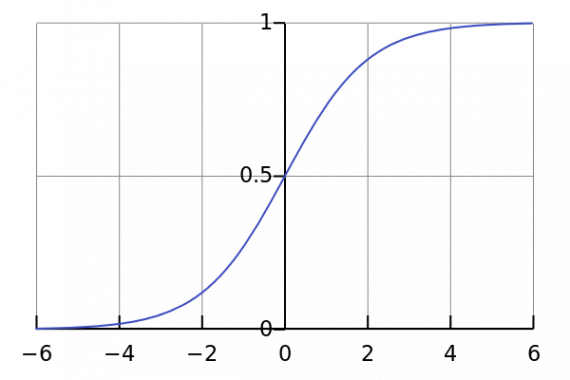
Сигмоида выглядит гладкой и подобна ступенчатой функции. Рассмотрим её преимущества.

Во-первых, сигмоида — нелинейна по своей природе, а комбинация таких функций производит тоже нелинейную функцию. Теперь мы можем стэкать слои.

Еще одно достоинство такой функции — она не бинарна, что делает активацию аналоговой, в отличие от ступенчатой функции. Для сигмоиды также характерен гладкий градиент.

Если вы заметили, в диапазоне значений X от -2 до 2 значения Y меняется очень быстро. Это означает, что любое малое изменение значения X в этой области влечет существенное изменение значения Y. Такое поведение функции указывает на то, что Y имеет тенденцию прижиматься к одному из краев кривой.

Сигмоида действительно выглядит подходящей функцией для задач классификации. Она стремиться привести значения к одной из сторон кривой (например, к верхнему при х=2 и нижнему при х=-2). Такое поведение позволяет находить четкие границы при предсказании.

Другое преимущество сигмоиды над линейной функцией заключается в следующем. В первом случае имеем фиксированный диапазон значений функции — [0,1], тогда как линейная функция изменяется в пределах (-inf, inf). Такое свойство сигмоиды очень полезно, так как не приводит к ошибкам в случае больших значений активации.

Сегодня сигмоида является одной из самых частых активационных функций в нейросетях. Но и у неё есть недостатки, на которые стоит обратить внимание.

Вы уже могли заметить, что при приближении к концам сигмоиды значения Y имеют тенденцию слабо реагировать на изменения в X. Это означает, что градиент в таких областях принимает маленькие значения. А это, в свою очередь, приводит к проблемам с градиентом исчезновения. Рассмотрим подробно, что происходит при приближении активационной функции к почти горизонтальной части кривой на обеих сторонах.

В таком случае значение градиента мало или исчезает (не может сделать существенного изменения из-за чрезвычайно малого значения). Нейросеть отказывается обучаться дальше или делает это крайне медленно (в зависимости от способа использования или до тех пор, пока градиент/вычисление не начнет страдать от ограничений на значение с плавающей точкой). Существуют варианты работы над этими проблемами, а сигмоида всё ещё очень популярна для задач классификации.

Гиперболический тангенс

Еще одна часто используемая активационная функция — гиперболический тангенс.

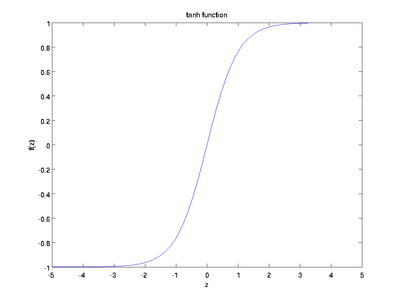
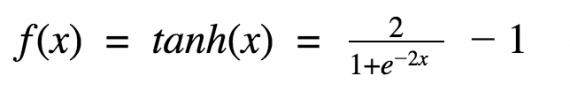
Гиперболический тангенс очень похож на сигмоиду. И действительно, это скорректированная сигмоидная функция.

Поэтому такая функция имеет те же характеристики, что и у сигмоиды, рассмотренной ранее. Её природа нелинейна, она хорошо подходит для комбинации слоёв, а диапазон значений функции -(-1, 1). Поэтому нет смысла беспокоиться, что активационная функция перегрузится от больших значений. Однако стоит отметить, что градиент тангенциальной функции больше, чем у сигмоиды (производная круче). Решение о том, выбрать ли сигмоиду или тангенс, зависит от ваших требований к амплитуде градиента. Также как и сигмоиде, гиперболическому тангенсу свойственная проблема исчезновения градиента.

Тангенс также является очень популярной и используемой активационной функцией.

ReLu

Следующая в нашем списке — активационная функция ReLu,

A(x) = max(0,x)

Пользуясь определением, становится понятно, что ReLu возвращает значение х, если х положительно, и 0 в противном случае. Схема работы приведена ниже.

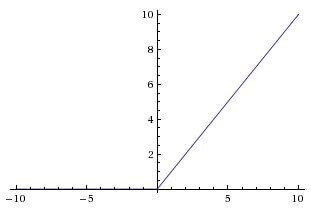
На первый взгляд кажется, что ReLu имеет все те же проблемы, что и линейная функция, так как ReLu линейна в первом квадранте. Но на самом деле, ReLu нелинейна по своей природе, а комбинация ReLu также нелинейна! (На самом деле, такая функция является хорошим аппроксиматором, так как любая функция может быть аппроксимирована комбинацией ReLu). Это означает, что мы можем стэкать слои. Область допустимых значений ReLu — [0,inf), то есть активация может “взорваться”.

Следующий пункт — разреженность активации. Представим большую нейронную сеть с множеством нейронов. Использование сигмоиды или гиперболического тангенса будет влечь за собой активацию всех нейронов аналоговым способом. Это означает, что почти все активации должны быть обработаны для описания выхода сети. Другими словами, активация плотная, а это затратно. В идеале мы хотим, чтобы некоторые нейроны не были активированы, это сделало бы активации разреженными и эффективными.

ReLu позволяет это сделать. Представим сеть со случайно инициализированными весами (или нормализированными), в которой примерно 50% активаций равны 0 из-за характеристик ReLu (возвращает 0 для отрицательных значений х). В такой сети включается меньшее количество нейронов (разреженная активация), а сама сеть становится легче. Отлично, кажется, что ReLu подходит нам по всем параметрам. Но ничто не безупречно, в том числе и ReLu.

Из-за того, что часть ReLu представляет из себя горизонтальную линию (для отрицательных значений X), градиент на этой части равен 0. Из-за равенства нулю градиента, веса не будут корректироваться во время спуска. Это означает, что пребывающие в таком состоянии нейроны не будут реагировать на изменения в ошибке/входных данных (просто потому, что градиент равен нулю, ничего не будет меняться). Такое явление называется проблемой умирающего ReLu (Dying ReLu problem). Из-за этой проблемы некоторые нейроны просто выключатся и не будут отвечать, делая значительную часть нейросети пассивной. Однако существуют вариации ReLu, которые помогают эту проблему избежать. Например, имеет смысл заменить горизонтальную часть функции на линейную. Если выражение для линейной функции задается выражением y = 0.01x для области x < 0, линия слегка отклоняется от горизонтального положения. Существует и другие способы избежать нулевого градиента. Основная идея здесь — сделать градиент неравным нулю и постепенно восстанавливать его во время тренировки.

ReLu менее требовательно к вычислительным ресурсам, чем гиперболический тангенс или сигмоида, так как производит более простые математические операции. Поэтому имеет смысл использовать ReLu при создании глубоких нейронных сетей.

Как выбрать функцию активации?

Настало время решить, какую из функций активации использовать. Следует ли для каждого случая использовать ReLu? Или сигмоиду? Или tanh? На эти вопросы нельзя дать однозначного ответа. Когда вы знаете некоторые характеристики функции, которую пытаетесь аппроксимировать, выбирайте активационную функцию, которая аппроксимирует искомую функцию лучше и ведет к более быстрому обучению.

Например, сигмоида хорошо показывает себя в задачах классификации (посмотрите еще раз на пункт про сигмоиду. Не присущи ли ей свойства идеального классификатора?), так как аппроксимацию классифицирующей функции комбинацией сигмоид можно провести легче, чем используя ReLu, например.

Используйте функцию, с которой процесс обучения и сходимость будут быстрее. Более того, вы можете использовать собственную кастомную функцию! Если вы не знаете природу исследуемой функции, в таком случае начните с ReLu и потом работайте в обратном направлении. В большинстве случаев ReLu работает как хороший аппроксиматор.

Создавайте уникальные видео, изображения и аватары с помощью онлайн-сервиса FabulaAI. Получите 10 бесплатных генераций сразу после регистрации!