В туториале показано, как с нуля построить искусственную нейронную сеть на Python с помощью библиотеки NumPy. Сеть будет классифицировать изображения из датасета Fruit360.
Материалы туториала, за исключением цветных изображений из сета Fruit360, взяты из книги «Practical Computer Vision Applications Using Deep Learning with CNNs» автора Ahmed Fawzy Gad.
Исходных код сети доступен странице автора на GitHub.
В туториале рассмотрен пример классификации изображений из датасета Fruit360 с помощью искусственной нейронной сети (Artificial Neural Network, ANN) — выбор признаков и реализация сети с нуля с помощью NumPy.
Объекты в наборе Fruit360 разбиты на 60 классов: яблоко, гуава, банан, финик, киви и другие категории фруктов. Мы будем работать с четырьмя классами: яблоко Braeburn, лимон Meyer, манго, малина. Каждый класс имеет порядка 491 изображений для обучения и 162 изображения для тестирования. Размер изображений 100х100 пикселей.
Извлечение признаков
Начнем с выбора подходящего набора признаков, чтобы достичь наибольшей точности классификации.
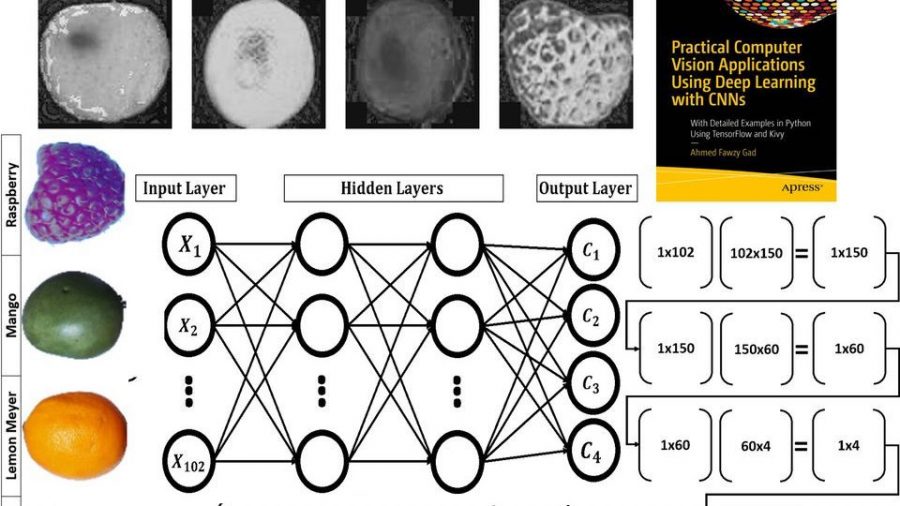
На рисунке ниже у объектов из 4 классов разные цвета. Поэтому цвет является подходящим признаком для данной задачи.

Пространство цветов RGB не изолирует информацию о цвете от другой информации, например, освещения. Если использовать RGB для представления изображения, в расчетах нужно учитывать все 3 канала. Поэтому намного удобнее работать с цветовым пространством HSV, которое изолирует информацию о цвете в единый канал. В таком случае за цвет отвечает канал hue (H), оттенок. Следующие изображения показывают, как будет выглядеть канал hue для примера фруктов, представленного выше. Значение оттенка отличается для каждого из изображений.
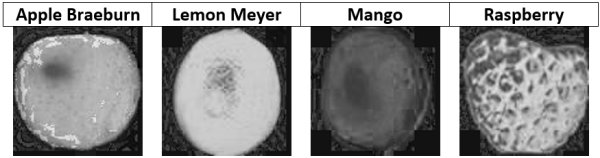
Канал hue также имеет размер 100×100 пикселей. Если в ANN использовать канал целиком, тогда входной слой должен иметь 10000 нейронов. Это большая сеть. Чтобы уменьшить количество используемых данных, можно использовать гистограмму для представления канала оттенка. Такая гистограмма будет иметь 360 ячеек (bin), что отражает количество возможных значений для канала hue.
Ниже представлена гистограмма для 4 выбранных фруктов. Каждому фрукту соответствует заполнение конкретной ячейки гистограммы. Теперь классы в данных меньше пересекаются друг с другом по выбранному признаку, чего нельзя сказать о цветовом пространстве RGB. Например, для яблока заполняются ячейки в диапазоне от 0 до 10, для манго — от 90 до 110. Поскольку в пространстве HSV между классами наблюдается такое различие в представлении, задача классификации упрощается, так как уменьшается неоднозначность, а качество предсказания увеличивается.

С помощью этого кода можно можно вывести диаграмму канала hue для 4 изображений.
import numpy
import skimage.io, skimage.color
import matplotlib.pyplot
raspberry = skimage.io.imread(fname="raspberry.jpg", as_grey=False)
apple = skimage.io.imread(fname="apple.jpg", as_grey=False)
mango = skimage.io.imread(fname="mango.jpg", as_grey=False)
lemon = skimage.io.imread(fname="lemon.jpg", as_grey=False)
apple_hsv = skimage.color.rgb2hsv(rgb=apple)
mango_hsv = skimage.color.rgb2hsv(rgb=mango)
raspberry_hsv = skimage.color.rgb2hsv(rgb=raspberry)
lemon_hsv = skimage.color.rgb2hsv(rgb=lemon)
fruits = ["apple", "raspberry", "mango", "lemon"]
hsv_fruits_data = [apple_hsv, raspberry_hsv, mango_hsv, lemon_hsv]
idx = 0
for hsv_fruit_data in hsv_fruits_data:
fruit = fruits[idx]
hist = numpy.histogram(a=hsv_fruit_data[:, :, 0], bins=360)
matplotlib.pyplot.bar(left=numpy.arange(360), height=hist[0])
matplotlib.pyplot.savefig(fruit+"-hue-histogram.jpg", bbox_inches="tight")
matplotlib.pyplot.close("all")
idx = idx + 1
Проходя в цикле через все изображения четырех классов, можно извлечь признаки со всех изображений. Следующий код проделывает это. В соответствии с числом изображений в 4 классах (1962) и длиной вектора признаков, извлеченных из каждого изображения (360), создаем массив NumPy из нулей и сохраняем его в переменной dataset_features.
Чтобы хранить метки классов для каждого изображения, создаем еще один NumPy массив и сохраняем его в переменной outputs. Яблоку соответствует метка 0, лимону — 1, манго — 2, малине — 3. Код запускается из корневой директории, в которой находятся 4 папки с именами, соответствующими названиям фруктов, записанным в списке fruits.
В коде проходится цикл по всем изображениям во всех папках:
- с каждого изображения извлекается диаграмма канала hue;
- каждому изображению приписывается метка класса;
- извлеченные признаки и метки классов сохраняются с помощью библиотеки pickle.
Можно также использовать NumPy для сохранения результирующих массивов.
import numpy
import skimage.io, skimage.color, skimage.feature
import os
import pickle
fruits = ["apple", "raspberry", "mango", "lemon"]
#492+490+490+490=1,962
dataset_features = numpy.zeros(shape=(1962, 360))
outputs = numpy.zeros(shape=(1962))
idx = 0
class_label = 0
for fruit_dir in fruits:
curr_dir = os.path.join(os.path.sep, fruit_dir)
all_imgs = os.listdir(os.getcwd()+curr_dir)
for img_file in all_imgs:
fruit_data = skimage.io.imread(fname=os.getcwd()+curr_dir+img_file, as_grey=False)
fruit_data_hsv = skimage.color.rgb2hsv(rgb=fruit_data)
hist = numpy.histogram(a=fruit_data_hsv[:, :, 0], bins=360)
dataset_features[idx, :] = hist[0]
outputs[idx] = class_label
idx = idx + 1
class_label = class_label + 1
with open("dataset_features.pkl", "wb") as f:
pickle.dump("dataset_features.pkl", f)
with open("outputs.pkl", "wb") as f:
pickle.dump(outputs, f)
Теперь каждое изображение представлено вектором признаков, состоящим из 360 элементов. Вектор фильтруется таким образом, чтобы сохранять наиболее релевантные элементы для разделения 4 классов. Новый укороченный вектор признаков имеет длину 102 вместо 360. Использование меньшего количества элементов помогает ускорить работу алгоритма. Переменная dataset_features будет иметь размер 1962х102.
Данные для тренировки (признаки и метки классов) готовы. Следующий шаг — реализация ANN с помощью NumPy.
Реализация нейронной сети
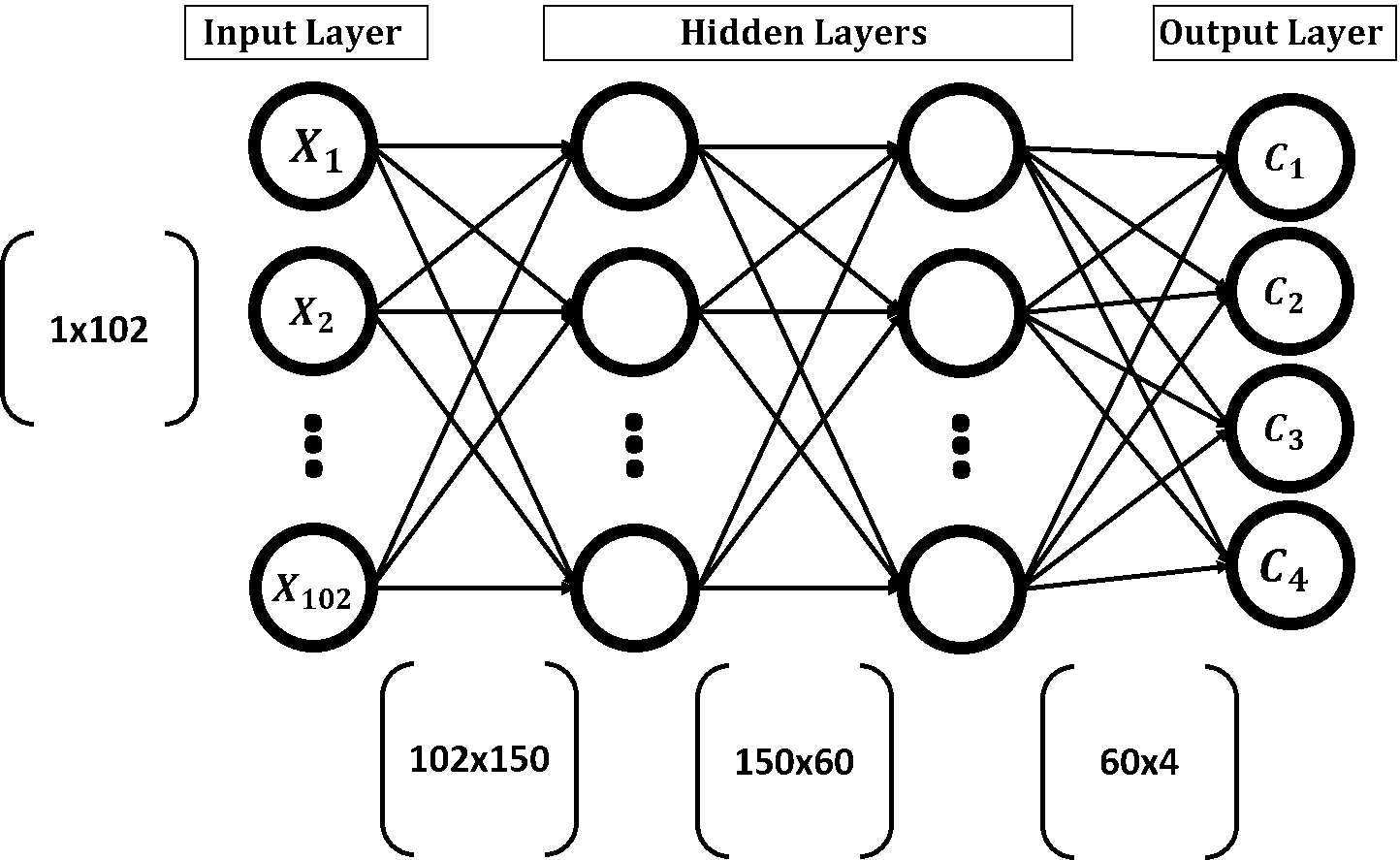
На рисунке представлена структура нейронной сети. Входной слой имеет 102 входных нейрона, два скрытых слоя состоят из 150 и 60 нейронов, соответственно, выходной слой имеет 4 выхода (по одному на каждый класс).
Входной вектор в любом слое умножается на матрицу весов; такая операция производит вектор локального выхода. Этот вектор выхода далее снова умножается на матрицу весов в следующем слое. Процесс продолжается до тех пор, пока не достигнут выходной слой. Лучше понять эту цепочку матричных перемножений помогает картинка:
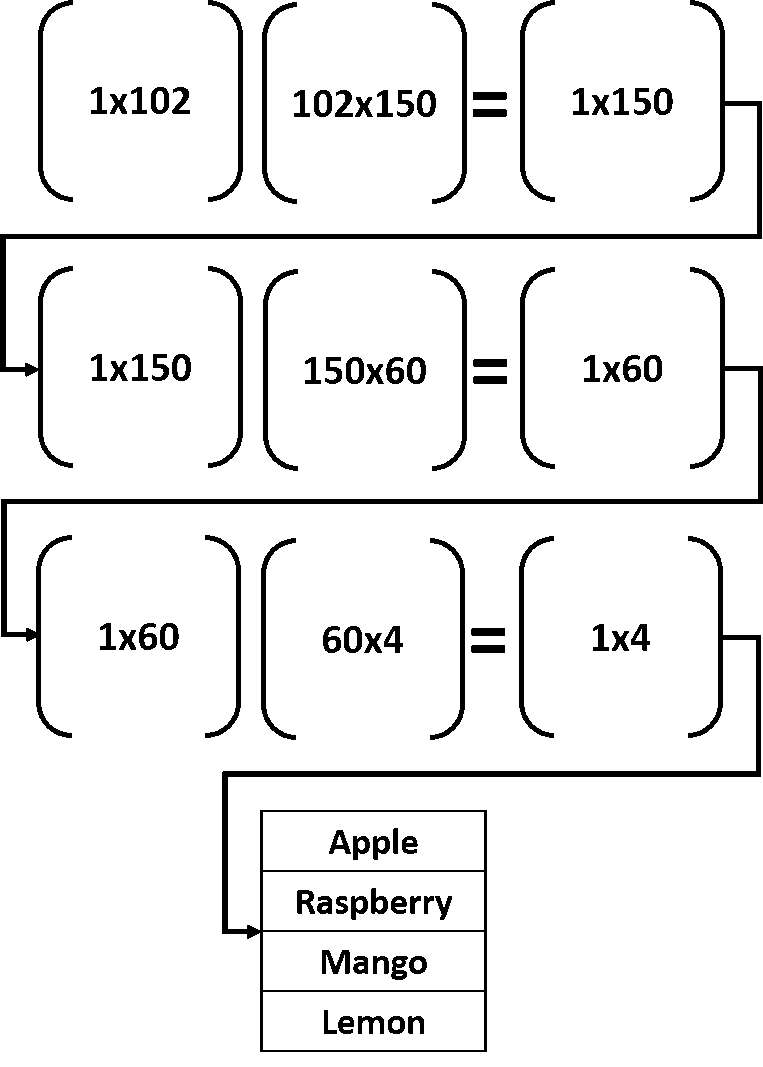
Входной вектор размера 1х102 умножается на матрицу весов первого скрытого слоя размером 102х150. Под умножением подразумевается матричное умножение. После этой операции на выходе получается массив 1х150. Такой массив далее используется в качестве входа, подаваемого на второй скрытый слой, где он умножается на матрицу весов размера 150х60. Результатом станет массив 1х60.
Затем этот массив умножается на весовую матрицу между вторым скрытым и выходным слоем, имеющую размер 60х4. Результатом таких операций станет вектор 1х4. Каждый элемент результирующем векторе соответствует определенному классу. Подаваемому на вход объекту приписывается метка, имеющая наибольшее значение в результирующем векторе.
Код, реализующий умножение, представлен ниже.
import numpy
import pickle
def sigmoid(inpt):
return 1.0 / (1 + numpy.exp(-1 * inpt))
f = open("dataset_features.pkl", "rb")
data_inputs2 = pickle.load(f)
f.close()
features_STDs = numpy.std(a=data_inputs2, axis=0)
data_inputs = data_inputs2[:, features_STDs > 50]
f = open("outputs.pkl", "rb")
data_outputs = pickle.load(f)
f.close()
HL1_neurons = 150
input_HL1_weights = numpy.random.uniform(low=-0.1, high=0.1,
size=(data_inputs.shape[1], HL1_neurons))
HL2_neurons = 60
HL1_HL2_weights = numpy.random.uniform(low=-0.1, high=0.1,
size=(HL1_neurons, HL2_neurons))
output_neurons = 4
HL2_output_weights = numpy.random.uniform(low=-0.1, high=0.1,
size=(HL2_neurons, output_neurons))
H1_outputs = numpy.matmul(a=data_inputs[0, :], b=input_HL1_weights)
H1_outputs = sigmoid(H1_outputs)
H2_outputs = numpy.matmul(a=H1_outputs, b=HL1_HL2_weights)
H2_outputs = sigmoid(H2_outputs)
out_otuputs = numpy.matmul(a=H2_outputs, b=HL2_output_weights)
predicted_label = numpy.where(out_otuputs == numpy.max(out_otuputs))[0][0]
print("Predicted class : ", predicted_label)
После считывания ранее сохраненных признаков и меток, фильтрации признаков определяются весовые матрицы в каждом слое. Им случайным образом приписываются значения в диапазоне от -0.1 до 0.1. Например, переменная input_HL1_weights хранит матрицу весов при переходе от входного к первому скрытому слою. Размер этой матрицы определяется в соответствии с количеством элементов в векторе признаков и числом нейронов в скрытом слое.
После создания матриц весов следующим шагом является матричное умножение. Переменная H1_outputs хранит выходы от перемножения вектора признаков выбранного объекта и матрицей весов между входным и первым скрытым слоями.
Обычно, чтобы выявить нелинейные зависимости между входами и выходами, функция активации применяется к выходам каждого скрытого слоя. Результаты матричного умножения проходят через сигмоидную функцию активации.
После генерации выходов на финальном слое делается предсказание. Предсказываемая метка класса сохраняется в переменной predicted_label. Все перечисленные выше шаги повторяются для каждого входного объекта. Полный код, проделывающий эту процедуру, представлен ниже.
import numpy
import pickle
def sigmoid(inpt):
return 1.0 / (1 + numpy.exp(-1 * inpt))
def relu(inpt):
result = inpt
result[inpt < 0] = 0
return result
def update_weights(weights, learning_rate):
new_weights = weights - learning_rate * weights
return new_weights
def train_network(num_iterations, weights, data_inputs, data_outputs, learning_rate, activation="relu"):
for iteration in range(num_iterations):
print("Itreation ", iteration)
for sample_idx in range(data_inputs.shape[0]):
r1 = data_inputs[sample_idx, :]
for idx in range(len(weights) - 1):
curr_weights = weights[idx]
r1 = numpy.matmul(a=r1, b=curr_weights)
if activation == "relu":
r1 = relu(r1)
elif activation == "sigmoid":
r1 = sigmoid(r1)
curr_weights = weights[-1]
r1 = numpy.matmul(a=r1, b=curr_weights)
predicted_label = numpy.where(r1 == numpy.max(r1))[0][0]
desired_label = data_outputs[sample_idx]
if predicted_label != desired_label:
weights = update_weights(weights,
learning_rate=0.001)
return weights
def predict_outputs(weights, data_inputs, activation="relu"):
predictions = numpy.zeros(shape=(data_inputs.shape[0]))
for sample_idx in range(data_inputs.shape[0]):
r1 = data_inputs[sample_idx, :]
for curr_weights in weights:
r1 = numpy.matmul(a=r1, b=curr_weights)
if activation == "relu":
r1 = relu(r1)
elif activation == "sigmoid":
r1 = sigmoid(r1)
predicted_label = numpy.where(r1 == numpy.max(r1))[0][0]
predictions[sample_idx] = predicted_label
return predictions
f = open("dataset_features.pkl", "rb")
data_inputs2 = pickle.load(f)
f.close()
features_STDs = numpy.std(a=data_inputs2, axis=0)
data_inputs = data_inputs2[:, features_STDs > 50]
f = open("outputs.pkl", "rb")
data_outputs = pickle.load(f)
f.close()
HL1_neurons = 150
input_HL1_weights = numpy.random.uniform(low=-0.1, high=0.1,
size=(data_inputs.shape[1], HL1_neurons))
HL2_neurons = 60
HL1_HL2_weights = numpy.random.uniform(low=-0.1, high=0.1,
size=(HL1_neurons, HL2_neurons))
output_neurons = 4
HL2_output_weights = numpy.random.uniform(low=-0.1, high=0.1,
size=(HL2_neurons, output_neurons))
weights = numpy.array([input_HL1_weights,
HL1_HL2_weights,
HL2_output_weights])
weights = train_network(num_iterations=10,
weights=weights,
data_inputs=data_inputs,
data_outputs=data_outputs,
learning_rate=0.01,
activation="relu")
predictions = predict_outputs(weights, data_inputs)
num_flase = numpy.where(predictions != data_outputs)[0]
print("num_flase ", num_flase.size)
Переменная weights хранит все веса нейросети. На основе размера каждой весовой матрицы структура сети может меняться динамически. Если размер переменной input_HL1_weights равен 102х80, то первый скрытый слой имеет 80 нейронов.
Главной функцией в нашем коде является train_network, так как в ней происходит обучение сети через прохождение в цикле по всем объектам датасета. Для каждого объекта выполняются рассмотренные выше шаги. Количество итераций, признаки, метки классов, веса, скорость обучения и функция активации остаются постоянными. В качестве функции активации берется ReLU или сигмоида. ReLU — функция с порогом значения, она возвращает входное значение, когда оно больше нуля. В противном случае ReLU возвращает 0.
Если сеть делает ошибочное предсказание для определенного объекта, веса обновляются с помощью функции update_weights. Для обновления весов не используется алгоритм оптимизации. Веса просто обновляются в соответствии с параметром learning rate (скорость обучения). Точность не превышает 45%. Для достижения лучшей точности уже используется алгоритм оптимизации. Например, в реализации ANN в библиотеке scikit-learn используется градиентный спуск.
