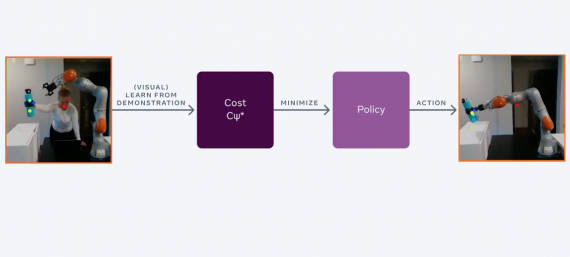
While a great number of researchers in Artificial Intelligence have focused their efforts on Deep Reinforcement Learning trying to beat human players on Atari games, researchers from the University of Toulouse and the University of York have proposed a different approach using Evolutionary Algorithms. Using Cartesian Genetic Programming (CGP) they achieve state-of-the-art results on a number of games and are competitive on many other.
Not only that this represents the first (as the authors’ report) use of Cartesian Genetic Programming as a game playing agent, but also one of the few studies where CGP is used in reinforcement learning tasks. Surprisingly, this evolutionary approach beats Deep Reinforcement Learning (Deep-Q Networks) approaches many benchmark games in the Arcade Learning Environment (ALE). Taking into account the fact that Deep RL methods have been applied to this problem for quite some time, gradually improving the results through many refinements, combining many techniques, the success of the proposed CGP approach is remarkable as it is the first attempt towards this problem.
What is Cartesian Genetic Programming?
As the name suggests, Cartesian Genetic Programming is a special form of Genetic Programming where programs are encoded as directed, acyclic graphs indexed by Cartesian Coordinates. The idea is to represent a program as a graph in which exist three types of nodes: input nodes, output nodes and functional nodes (which are defined by a set of evolved genes) in a Cartesian coordinate system. The functional nodes encode an operation (function) and connect to input nodes or other functional nodes via their cartesian coordinates.
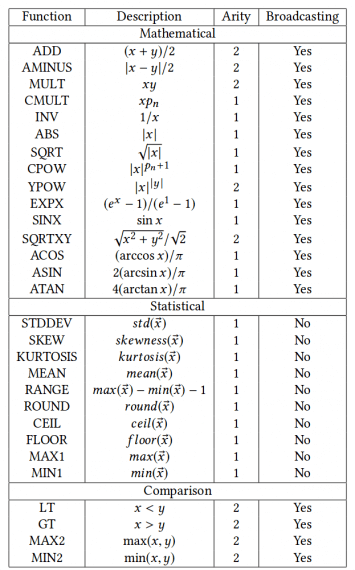
As in all evolutionary algorithms, defining a proper genotype is very important and sometimes crucial in the process of finding an optimal solution by evolution. In CGP, the choice of a function set is important and in this work, many of the standard mathematical and comparison functions are used as well as a list of list processing functions. The researchers tried to keep the function set as simple as possible, however, they report that the function set used in this work is pretty large and they leave the search for a minimal necessary function set as a future work. The function set used is given in the tables below.
The Method
The Arcade Learning Environment (ALE) provides games where playing can be seen as processing an image input and giving a specific command for playing at different time step. As mentioned before, playing Arcade games requires learning how to play by maximizing the game score. That is why RL has been used in most of the previous approaches as well as in this work.
The Genotype
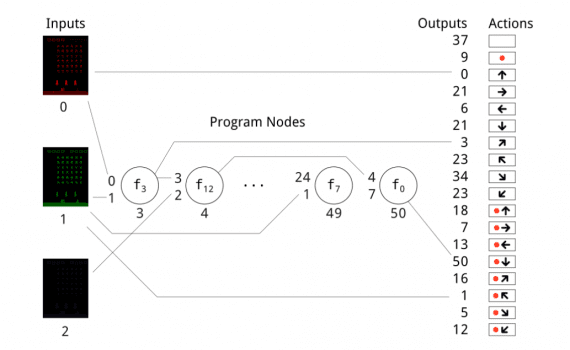
As discussed above, in CGP a program is defined by a graph, and this graph is positioned in a rectangular grid with R rows and C columns. Each node is allowed to connect to any node of the previous columns based on a distance – connectivity parameter. A node is represented by four float numbers in the range [0.0, 0.1] corresponding to x input, y input, function, p parameter. The x and y values are used to determine the inputs to n. The function gene is cast to an integer and used to index into the list of available functions, determining the function that the node uses. The parameter p is passed to the function as additional input as some functions require.
In the Cartesian grid, C columns are used and 1 row, where all the nodes are arranged. It starts with input nodes that are not evolved and continues with functional nodes ordered by the ordering in the genome. Output genes are rounded down to determine the indices of the nodes which will give the final program output. Each node in the graph has an output value, which is initially set to the scalar 0. At each step, first, the output values of the program input nodes are set to the program inputs. Then, the function of each program node is computed once, using the outputs from connected nodes of the previous step as inputs. The scheme of an active graph is given in the image.
Evolution
At initialization, a random genome is created using G uniformly distributed values in [0.0, 1.0]. This individual is evaluated and is considered the first elite individual. At each generation, λ offspring are generated using genetic mutation. These offspring are each evaluated and, if their fitness is greater than or equal to that of the elite individual, they replace the elite. This process is repeated until Neval individuals have been evaluated; in other words, for Neval / λ generations.
Evolution Parameters
The genetic mutation operator randomly selects M nodes of the program node genes and sets them to new random values, drawn from a uniform random distribution in [0.0, 1.0]. The final parameters used are:
- C = 40 (40 active nodes)
- r = 0.1
- λ = 10 (number of offspring generated at each generation).
- M nodes = 0.1
- M output = 0.6
Playing Atari Games
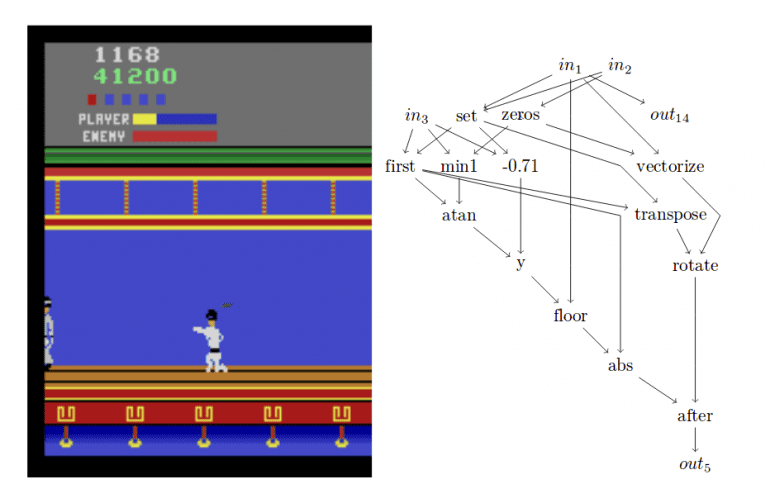
Given the genotype and evolution parameters, the CGP approach was evaluated on Arcade Games in the ALE environment where exist 18 actions: directional movements of the controller (8), button pressing (1), no action (1), and controller movement while button pressing (8). The ALE game screen is represented by RGB channels of a sequence of images defining the input to the method. To be able to compare with human-players frame skipping was introduced with the probability of 0.25 to simulate delay or control lag.
The success of many of the arcade games is explained by the researchers by the evolution process which selects individuals based on their overall performance and not based on individual actions. The policy which the agent represents will, therefore, tend towards actions which, on average, give very good rewards. In the paper, they show that the agents very often employ simple playing strategies, that are on average effective.
In conclusion, the success of Cartesian Genetic Programming in RL task is remarkable and its capability to evolve simple, yet effective programs is very clear. This interesting approach raises again the question if we need evolutionary algorithms to push further the capabilities of AI.