From a data structure point of view, point clouds are unordered sets of vectors. They are specific and differ very much from other data types such as images and videos. Still, many sensors such as Microsoft’s Kinect, LIDAR (used in the autonomous driving industry) provide a point cloud as output data. This kind of specific data requires specific data processing techniques that will be able to exploit and extract as much information as possible.
Typically, a convolutional neural network operates using 2D image data, and it learns by taking pixels as input. Over time, researchers in the deep learning community have found ways to use a different kind of data such as videos, binary images, etc., with convolutional architectures. Convolutional neural networks are designed and proved to be very successful in exploiting the spatiality in the data, i.e., capturing the spatial information. They are able to learn a hierarchy of features directly from the pixel data by applying kernel operations in well-defined local regions (called local receptive fields).
Talking about the spatial information, we have seen that convolutional neural networks achieved greater success with 2D data than 3D spatial data and this raises a question — “Why CNNs are worse with 3D data?”.
Well, recently two types of CNN networks have been developed for learning over 3D data: volumetric representation-based CNNs and multi-view based CNNs. Empirical results have shown that there is a considerable gap between the two and that existing volumetric CNN architectures are unable to fully exploit the power of 3D representations. This comes mostly from the computational and storage costs of the network, that grows cubically with the input resolution. In this context, processing of point clouds (which represent 3D spatial data) is very computationally costly, and 3D-CNN architectures have been applied only to low input resolution point clouds ranging from 30x30x30 to 256x256x256. 3D-CNN kernels typically are applied to volumetric representations of 3D data, which makes the task of learning over point clouds even more difficult and unfeasible.
In a novel approach, researchers from the University of Western Australia proposed an innovative way of handling point clouds in CNNs by introducing spherical convolutions. The key idea is to traverse the 3D space with a spherical kernel and partition the space using octree data structure.
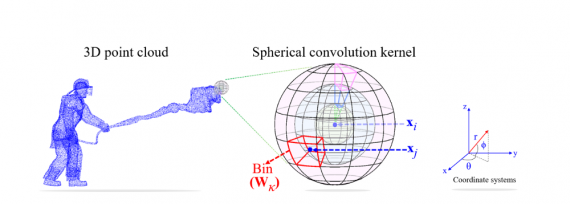
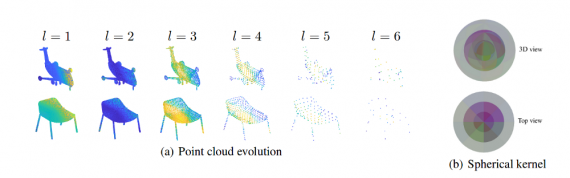
According to the authors, spherical regions are suitable for computing geometrically meaningful features from unstructured 3D data. They propose an approach that takes each point in space (with x, y, z coordinates) and defines a spherical region around it. Then, they divide the sphere into n x p x qbins by partitioning the space uniformly along azimuth and elevation dimensions. For each of the bins, they define a weight matrix of learnable parameters(weights). Together these matrices from all the bins form a single spherical convolutional kernel. To compute the activation of a single point in the point cloud, they take the relevant weight matrices of all neighbouring points (which are defined as neighbourhood points if they exist in the sphere). Then they represent each of the nearby points with the relative spherical coordinates to the point of interest.
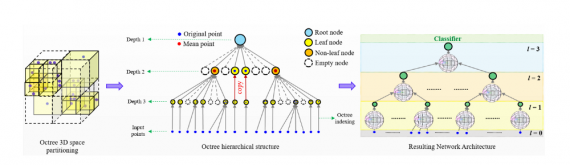
Since point clouds are not in a regular format, most researchers typically transform such data to regular 3D voxel grids or collections of images (e.g, views) before feeding them to a deep net architecture. In contrast, the authors use a different approach by representing the point cloud with octree structure. As mentioned before, this is less costly in terms of computation and storage than voxel grids as a volumetric representation and moreover, it can successfully handle irregular 3D point clouds (Note: most of the point clouds coming from sensors are irregular having highly variable point density). They use an octree of depth L, where each depth level represents a partitioning of the 3D space — from coarser to finer (top to bottom). The network is trained such that kernels are applied in the neighbourhood of each point. The matrices assigned to each bin when applying the kernel are learned during training and they represent the weights.
Evaluation and Conclusions
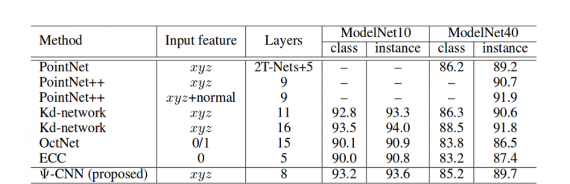
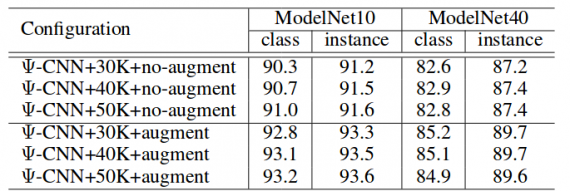
This work shows promising results in the classification of objects in (irregular) 3D point clouds. The evaluation was done on the standard benchmark datasets comparing with state-of-the-art methods. The architecture outperforms ECC and OctNet but fails to outperform the PointNet which is current state-of-the-art network architecture evaluated on ModelNet10 and ModelNet40. Also, the training experiments presented show that data augmentation improves results significantly.
Finally, this approach shows very good results for what seems to be a very difficult task: finding an efficient way to use convolutional neural networks with 3D point clouds. In fact, it shows that the difficulty in the learning of the point cloud structure can be reduced by keeping and learning a set of points that represent the skeleton of an object. Thus, a suitable data representation (that will capture this) is necessary and in this case, it is the octree. The authors show the evolution of the point cloud as a function of the depth of the octree.
The novel approach opens the doors for further investigation and use of non-conventional deep learning techniques (like the spherical kernel) as well as efficient processing of irregular 3D point cloud data. It shows that a point cloud can be processed with a convolutional neural network in a scalable manner, proving that with the results on the task of object recognition.