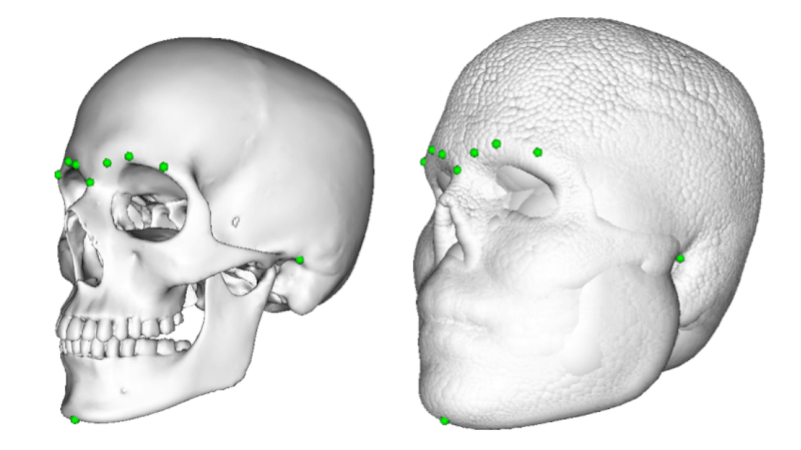
Facial reconstruction is mainly used in two principal branches of science: forensic science and anthropology. Remains of a human skull act as input to reconstruct the most likely corresponding facial appearance of the dead person to enable recognition. Traditional methods rely on manual sculpturing a moldable substance onto the replica of the unknown skull using anatomic clues and reference data.
Previous Work
Computer-aided facial reconstruction methods have been previously proposed. Related work uses different techniques for the underlying registration as well as for the subsequent facial reconstruction. Turner in A novel method of automated skull registration for forensic facial approximation introduced a technique for automated skull registration and craniofacial reconstruction based on extracted surfaces from CT data that was applied to a large CT database consisting of 280 individuals. For registration of a known skull to a question one, the authors use a heuristic to find crest lines in combination with a two-step ICP registration followed by a thin-plate spline warping process.
Shui in Densely Calculated Facial Soft Tissue Thickness for Craniofacial Reconstruction in Chinese Adults presented an approach for craniofacial reconstruction based on dense FSTT statistics, utilizing CT data. Their method depends on 78 manually selected and marks placed on the skull, which guides the course registration of a template skull to each skull, followed by a fine registration using ICP and thin plate splines (TPS).
The FSTT measurement is performed for each vertex of the deformed skull in the direction defined by the geometric coordinate. A coarse reconstruction of a face from an unidentified skull is achieved by translating each skull vertex in the specified direction by the length of the FSTT measured at this position. To achieve a smooth appearance, six additional points have to be marked manually for guiding a TPS deformation of a template face to the coarse reconstruction. Finally, the recovery of mouth, eyes, and nose has to be performed by a forensic expert, which makes the method not fully automatic.
State-of-the-art Idea
The approach to forensic facial reconstruction is divided into two parts: model generation and forensic facial reconstruction. The method is fully automated, from the initial skull registration up to the final face reconstruction, and thus does not require any manual interaction. Only the initial model generation (preprocessing or training phase) requires a few manual steps. Below are the three models as are necessary for automated facial reconstruction approach:
- the parametric skull model,
- the statistic of FSTT, and
- the parametric head model.
Model generation
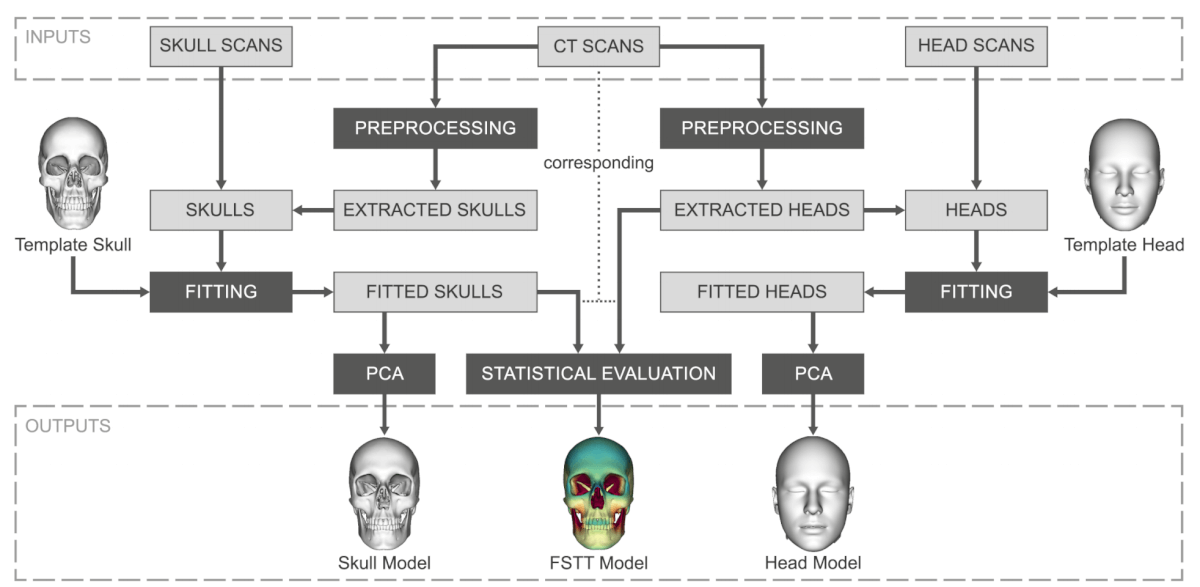
The next step is to establish the relationship between different skulls as well as between different heads. For this purpose, in a fitting process, an appropriate template model is registered to each given mesh of a specific input type. After that, we can utilize the fitted templates to determine the geometric variability of the skulls respectively heads performing a PCA. As result, we derive two parametric models: a parametric skull model and a parametric head model. Based on corresponding skulls and heads extracted from CT scans, a dense FSTT map is built in the statistical evaluation step.
Generating a parametric skull model
To generate a parametric skull model, a relationship is established between the different skulls from our database. For this purpose, a single template skull is a register to each skull individually. This template model has to be a volumetric tetrahedral mesh to accurately represent the solid nature of a bony skull. The fitting process comprises the following two main stages for an input skull with vertex positions P={p1,…,pM}:
- A rigid global transformation that coarsely aligns the input skull to the template skull. The registration starts with the fast global registration approach, followed by a refinement step using the well known Iterative Closest Point(ICP) algorithm
- A fine registration of the template skull to the input skull, which consists of several non-rigid transformation steps, computed by minimizing the energy:
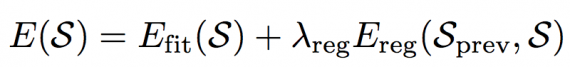
consisting of a fitting term E(fit) and a regularization term E(reg). In the non-rigid step, the fitting term is :
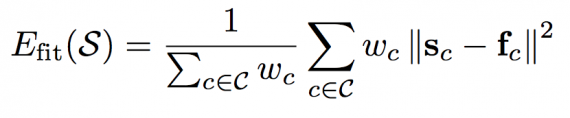
penalizes the squared distance between a vertex on the template skull s(c) and its corresponding point f(c), which is a point on or close to the mesh of the input skull. The regularization term
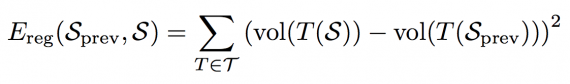
penalizes geometric distortion of the template skull during the fitting.
Generating a statistic of a facial soft tissue thickness
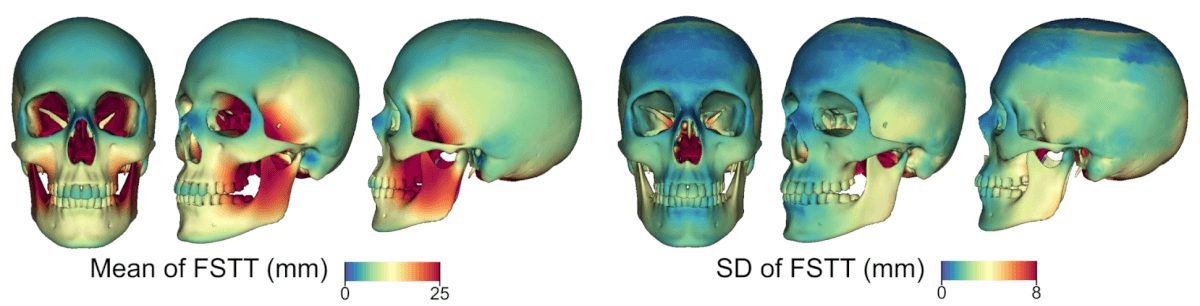
In a statistical evaluation process, the distances between 43 corresponding skulls and heads extracted from the CT scans are measured. To this end, each vertex is determined of a fitted skull the shortest distance to the surface of the extracted skin surface. Finally, the mean and standard deviation of the FSTT are computed per vertex. Fig 2 shows the mean skull ̄s with color-coded mean and standard deviation of the obtained FSTT.
Generating a parametric head model
Similar to the skull model, the parametric head model is generated by fitting a template head to head scans of real subjects, which establishes the correspondence between them, and then perform statistical analysis using PCA. For the model generation, the skin surfaces are extracted from the 43 CT scans used for building the FSTT statistics (26 male, 17 female). In the following, a head scan (extracted from CT or generated through the optical scan) is represented by its point set Q={q1,…,qN}. Since the head models are skin surfaces only, the head template is a surface triangle mesh consisting of n≈6 k vertices with positions H={h1,…,hn}. The template fitting process consists of two stages, similar to the skull fitting:
- We first optimize scaling, rotation, and translation of the template model to align it to the point set Q by minimizing the sum of squared distances between points q(c) on the point set Q and their corresponding points h(c) on the template model H using ICP.
- After this coarse initialization, we perform a fine-scale non-rigid registration to update the vertex positions H, such that the template model better fits the points Q. The non-linear objective function is
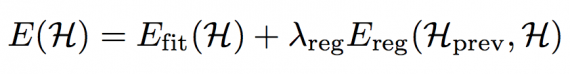
The fitting term E(fit) penalizes squared distances between points qc on the point set Q and corresponding points hc on the template model H:
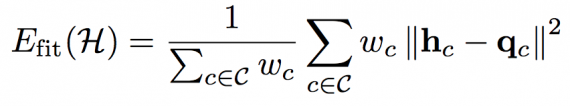
The regularization term E(reg) penalizes the geometric distortion of the undeformed model H(prev) (the result of the previous rigid/similarity transformation) to the deformed state H.
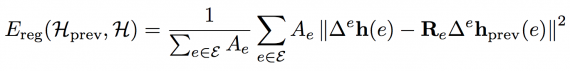
Conclusion
In this Research, an automated method based on a parametric skull model, a parametric head model, and a statistic of FSTT for reconstructing the face for a given skull is presented.
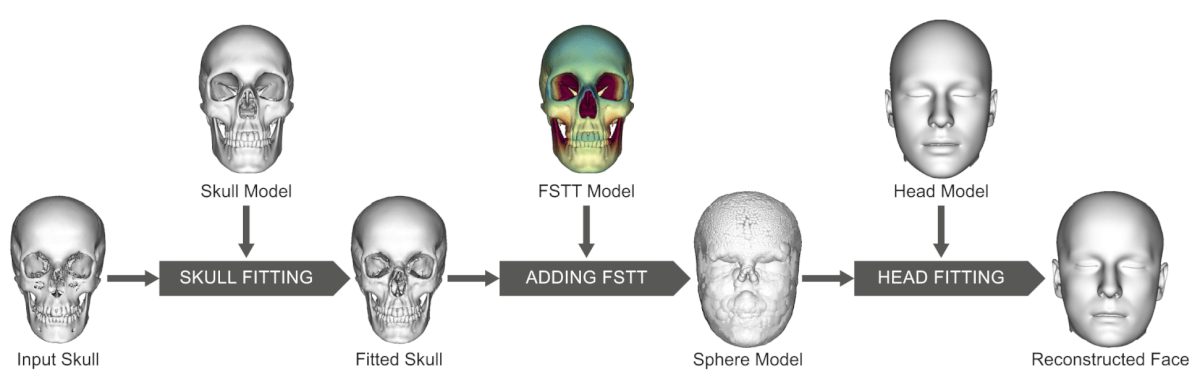
The automated technique suggested aids recognition of unknown skull remains by providing statistical estimates derived from a CT head database and 3D surface scans. By creating a range of plausible heads in the sense of statistical estimates, a “visual guess” of likely heads can be used for recognition of the individual represented by the unknown skull.
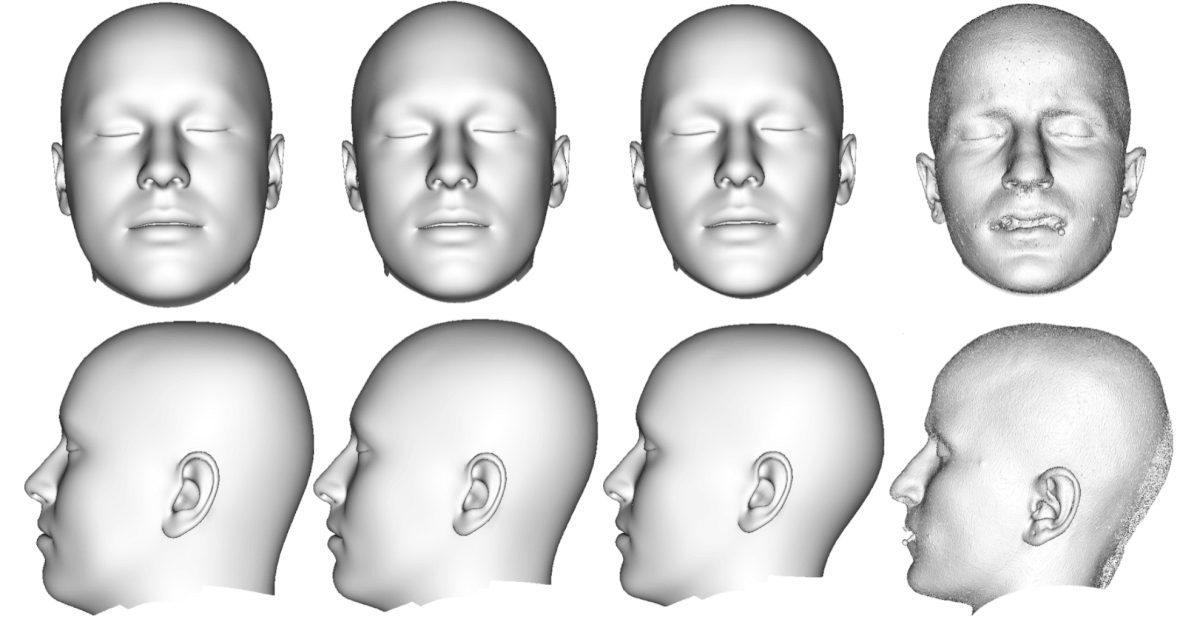
The main advantage of this approach over landmark-based FSTT measurements is the density of the FSTT map without the need for normal error-prone information. For any vertex of the parametric skull model, an FSTT value can be derived from the statistic of FSTT.


