Градиентый бустинг — просто о сложном

Хотя большинство победителей соревнований на Kaggle используют композицию разных моделей, одна из них заслуживает особого внимания, так как является почти обязательной частью. Речь, конечно, про Градиентный бустинг (GBM) и его вариации. Возьмем, например. победителя Safe Driver Prediction, Michael Jahrer. Его решение — это комбинация шести моделей. Одна LightGBM (вариация GBM) и пять нейронных сетей. Хотя его успех в большей мере принадлежит полуконтролируемому обучению, которое он использовал для упорядочивания данных, градиентный бустинг сыграл свою роль.

Даже несмотря на то, что градиентный бустинг используется повсеместно, многие практики до сих пор относятся к нему, как к сложному алгоритму в черном ящике и просто запускают готовые модели из предустановленных библиотек. Цель этой статьи — дать понимание как же работает градиентный бустинг. Разбор будет посвящен чистому “vanilla” GMB.

Ансамбли, бэггинг и бустинг

Когда мы пытаемся предсказать целевую переменную с помощью любого алгоритма машинного обучения, главные причины отличий реальной и предсказанной переменной — это noise, variance и bias. Ансамбль помогает уменьшить эти факторы (за исключением noise — это неуменьшаемая величина).

Ансамбль

Ансамбль — это набор предсказателей, которые вместе дают ответ (например, среднее по всем). Причина почему мы используем ансамбли — несколько предсказателей, которые пытаюсь получить одну и ту же переменную дадут более точный результат, нежели одиночный предсказатель. Техники ансамблирования впоследствии классифицируются в Бэггинг и Бустинг.

Бэггинг

Бэггинг — простая техника, в которой мы строим независимые модели и комбинируем их, используя некоторую модель усреднения (например, взвешенное среднее, голосование большинства или нормальное среднее).

Обычно берут случайную подвыборку данных для каждой модели, так все модели немного отличаются друг от друга. Выборка строится по модели выбора с возвращением. Из-за того что данная техника использует множество некореллириющих моделей для построения итоговой модели, это уменьшает variance. Примером бэггинга служит модель случайного леса (Random Forest, RF)

Бустинг

Бустинг — это техника построения ансамблей, в которой предсказатели построены не независимо, а последовательно

Это техника использует идею о том, что следующая модель будет учится на ошибках предыдущей. Они имеют неравную вероятность появления в последующих моделях, и чаще появятся те, что дают наибольшую ошибку. Предсказатели могут быть выбраны из широкого ассортимента моделей, например, деревья решений, регрессия, классификаторы и т.д. Из-за того, что предсказатели обучаются на ошибках, совершенных предыдущими, требуется меньше времени для того, чтобы добраться до реального ответа. Но мы должны выбирать критерий остановки с осторожностью, иначе это может привести к переобучению. Градиентный бустинг — это пример бустинга.

Алгоритм градиентного бустинга

Градиентный бустинг — это техника машинного обучения для задач классификации и регрессии, которая строит модель предсказания в форме ансамбля слабых предсказывающих моделей, обычно деревьев решений.

Цель любого алгоритма обучения с учителем — определить функцию потерь и минимизировать её. Давайте обратимся к математике градиентного бустинга. Пусть, например, в качестве функции потерь будет среднеквадратичная ошибка (MSE):

Мы хотим, чтобы построить наши предсказания таким образом, чтобы MSE была минимальна. Используя градиентный спуск и обновляя предсказания, основанные на скорости обучения (learning rate), ищем значения, на которых MSE минимальна.

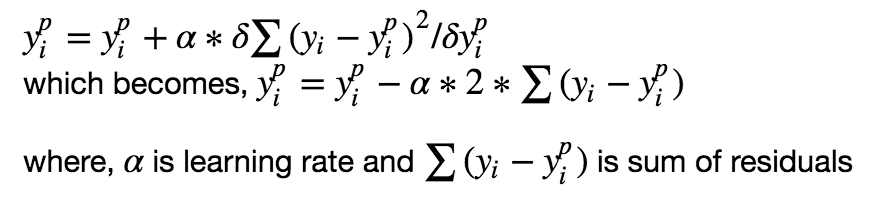
Итак, мы просто обновляем предсказания таким образом, что сумма наших отклонений стремилась к нулю и предсказанные значения были близки к реальным.

Интуиция за градиентным бустингом

Логика, что стоит за градиентым бустингом, проста, ее можно понять интуитивно, без математического формализма. Предполагается, что читатель знаком с простой линейной регрессией.

Первое предположение линейной регресии, что сумма отклонений = 0, т.е. отклонения должны быть случайно распределены в окрестности нуля.

Теперь давайте думать о отклонениях, как об ошибках, сделанных нашей моделью. Хотя в моделях основанных на деревьях не делается такого предположения, если мы будем размышлять об этом предположении логически (не статистически), мы можем понять, что увидив принцип распределения отклонений, сможем использовать данный паттерн для модели.

Итак, интуиция за алгоритмом градиентного бустинга — итеративно применять паттерны отклонений и улучшать предсказания. Как только мы достигли момента, когда отклонения не имеют никакого паттерна, мы прекращаем достраивать нашу модель (иначе это может привести к переобучению). Алгоритмически, мы минимизируем нашу функцию потерь.

В итоге,

• Сначала строим простые модели и анализируем ошибки;
• Определяем точки, которые не вписываются в простую модель;
• Добавляем модели, которые обрабатывают сложные случаи, которые были выявлены на начальной модели;
• Собираем все построенные модели, определяя вес каждого предсказателя.

Шаги построения модели градиентного спуска

Рассмотрим смоделированные данные, как показано на диаграмме рассеивания ниже с 1 входным (x) и 1 выходной (y) переменными.

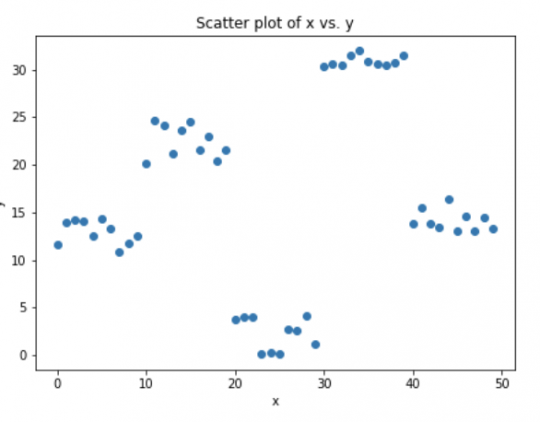
Данные для показанного выше графика генерируются с использованием кода python:

1. Установите линейную регрессию или дерево решений на данные (здесь выбрано дерево решений в коде) [вызов x как input и y в качестве output]

2. Вычислите погрешности ошибок. Фактическое целевое значение, минус прогнозируемое целевое значение [e1 = y — y_predicted1]

3. Установите новую модель для отклонений в качестве целевой переменной с одинаковыми входными переменными [назовите ее e1_predicted]

4. Добавьте предсказанные отклонения к предыдущим прогнозам
[y_predicted2 = y_predicted1 + e1_predicted]

5. Установите еще одну модель оставшихся отклонений. т.е. [e2 = y — y_predicted2], и повторите шаги с 2 по 5, пока они не начнутся overfitting, или сумма не станет постоянной. Управление overfitting-ом может контролироваться путем постоянной проверки точности на данных для валидации.

Чтобы помочь понять базовые концепции, вот ссылка с полной реализацией простой модели градиентного бустинга с нуля.

Приведенный код — это неоптимизированная vanilla реализация повышения градиента. Большинство моделей повышения градиента, доступных в библиотеках, хорошо оптимизированы и имеют множество гиперпараметров.

Визуализация работы Gradient Boosting Tree:

• Синие точки (слева) отображаются как вход (x) по сравнению с выходом (y);
• Красная линия (слева) показывает значения, предсказанные деревом решений;
• Зеленые точки (справа) показывают остатки по сравнению с вводом (x) для i-й итерации;
• Итерация представляет собой последовательное заполнения дерева Gradient Boosting.

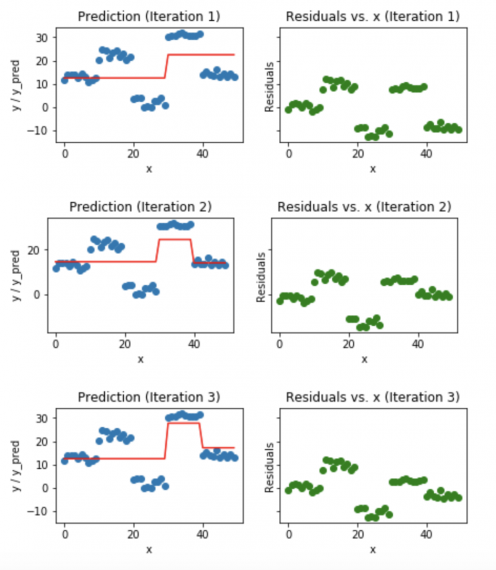
Заметим, что после 20-й итерации отклонения распределены случайным образом (здесь не говорим о случайной норме) около 0, и наши прогнозы очень близки к истинным значениям (итерации называются n_estimators в реализации sklearn). Возможно, это хороший момент для остановки, или наша модель начнет переобучаться.

Посмотрим, как выглядит наша модель после 50-й итерации.

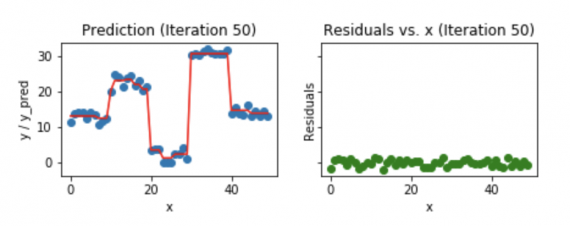
Мы видим, что даже после 50-й итерации отклонения по сравнению с графиком x похожи на то, что мы видим на 20-й итерации. Но модель становится все более сложной, и предсказания перерабатывают данные обучения и пытаются изучить каждый учебный материал. Таким образом, было бы лучше остановиться на 20-й итерации.

Фрагмент кода Python, используемый для построения всех вышеперечисленных графиков.

Видео Александра Ихлера:

Генерируйте видео, изображения и аватары с помощью сервиса FabulaAI. Получите 10 бесплатных генераций сразу после регистрации!