Как применять теорему Байеса для решения реальных задач

Возможно, вы никогда не слышали про теорему Байеса, но пользовались ей постоянно. Например, изначально вы оценили вероятность получения прибавки к зарплате как 50%. Получив положительные отзывы от менеджера, вы скорректировали оценку в лучшую сторону, и, наоборот, уменьшили ее, если сломали кофеварку на работе. Так происходит уточнение значения вероятности по мере аккумулирования информации.

Основная идея теоремы Байеса состоит в том, чтобы получить большую точность оценки вероятности события путем учета дополнительных данных.

Принцип прост: есть первоначальная основная оценка вероятности, которую уточняют c получением большего количества информации.

Формула Байеса

Интуитивные действия формализуются в простом, но мощном уравнении (формула вероятности Байеса):

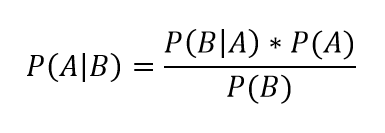
Левая часть уравнения — апостериорная оценка вероятности события А при условии наступления события В (т. н. условная вероятность).

• P(A)  — вероятность события А (основная, априорная оценка);
• P(B|A) — вероятность (также условная), которую мы получаем из наших данных;
• а P(B) — константа нормировки, которая ограничивает вероятность значением 1.

Это короткое уравнение является основой байесовского метода.

Абстрактность событий А и В не позволяет четко осознать смысл этой формулы. Для понимания сути теоремы Байеса рассмотрим реальную задачу.

Пример

Одной из тем, над которой я работаю, является изучение моделей сна. У меня есть данные за два месяца, записанные с помощью моих часов Garmin Vivosmart, показывающие, во сколько я засыпаю и просыпаюсь. Окончательная модель, показывающая наиболее вероятное распределение вероятности сна как функцию времени (MCMC — приблизительный метод), приведена ниже.

На графике приведена вероятность того, что я сплю, в зависимости лишь от времени. Как она изменится, если учесть время, в течение которого включен свет в спальне? Для уточнения оценки и нужна теорема Байеса. Уточненная оценка основана на априорной и имеет вид:

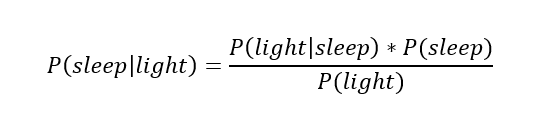
Выражение слева — вероятность того, что я сплю, при условии, что известно, включен ли свет в моей спальне. Априорная оценка в данный момент времени (приведена на графике выше) обозначена как P(sleep). Например, в 10:00 вечера априорная вероятность того, что я сплю, равна 27,34%.

Добавим больше информации, используя вероятность P(bedroom light|sleep), полученную из наблюдаемых данных.

Из собственных наблюдений мне известно следующее: вероятность того, что я сплю, когда свет включен, равна 1%.

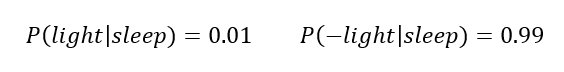
Вероятность того, что свет выключен во время сна, равна 1-0,01 = 0,99 (знак «-» в формуле означает противоположное событие), потому что сумма вероятностей противоположных событий равна 1. Когда я сплю, то свет в спальне либо включен, либо выключен.

Наконец, уравнение также включает в себя константу нормировки P(light) — вероятность того, что свет включен. Свет бывает включен и когда я сплю, и когда бодрствую. Поэтому, зная априорную вероятность сна, вычислим константу нормировки так:

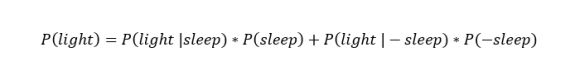
Вероятность того, что свет включен, учтена в обоих вариантах: либо я сплю, либо нет (P (-sleep) = 1 — P (sleep) — это вероятность того, что я не сплю.)

Вероятность того, что свет включен в тот момент, когда я не сплю, равна P(light|-sleep), и определяется путем наблюдения. Мне известно, что свет горит, когда я бодрствую, с вероятностью 80% (это означает, что есть 20% вероятность того, что свет не включен, если я бодрствую).

Окончательное уравнение Байеса принимает вид:

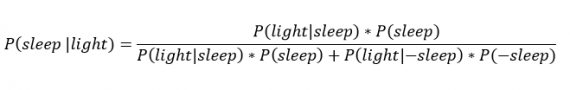
Оно позволяет вычислить вероятность того, что я сплю, при условии, что свет включен. Если нас интересует вероятность того, что свет выключен, нужно каждую конструкцию P(light|… заменить на P(-light|….

Давайте посмотрим, как используют полученные символьные уравнения на практике.

Применим формулу к моменту времени 22:30 и учтем, что свет включен. Мы знаем, вероятность того, что я спал, равна 73,90%. Это число — отправная точка для нашей оценки.

Уточним его, учтя информацию об освещении. Зная, что свет включен, подставим числа в формулу Байеса:

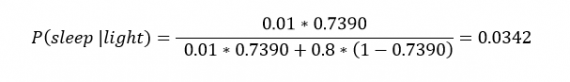
Дополнительные данные резко изменили оценку вероятности: от более 70% до 3,42%. Это показывает силу теоремы Байеса: мы смогли уточнить нашу первоначальную оценку ситуации, включив в нее больше информации. Возможно, мы уже интуитивно делали это раньше, но теперь, рассуждая об этом в терминах формальных уравнений, мы смогли подтвердить наши прогнозы.

Python

Рассмотрим еще один пример. Что если на часах 21:45 и свет выключен? Попытайте рассчитать вероятность самостоятельно, считая априорную оценку равной 0.1206.

Вместо того, чтобы каждый раз считать вручную, я написал простой код на Python для выполнения этих вычислений, который вы можете попробовать в Jupyter Notebook. Вы получите следующий ответ:

Time: 09:45:00 PM            Light is OFF.

The prior probability of sleep: 12.06%
The updated probability of sleep: 40.44%

И снова дополнительная информация меняет нашу оценку. Теперь, если моя сестра захочет позвонить мне в 21:45 зная, что мой свет включен, она может воспользоваться этим уравнением, чтобы определить, смогу ли я взять трубку (предполагая, что я беру трубку только бодрствующим)! Кто говорит, что статистика неприменима повседневной жизни?

Визуализация вероятности

Наблюдение за вычислениями полезно, но визуализация помогает добиться более глубокого понимания результата. Я всегда стараюсь использовать графики, чтобы генерировать идеи, если они сами не приходят при простом изучении уравнений. Мы можем визуализировать априорное и апостериорное распределения вероятности сна с использованием дополнительных данных:

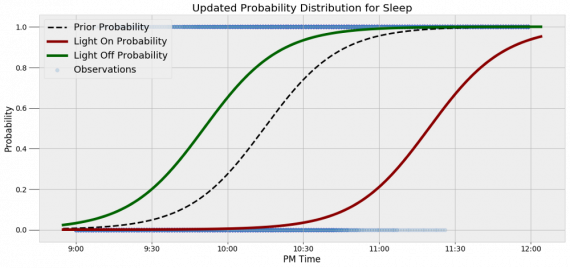
Когда свет включен, график смещается вправо, указывая на то, что я с меньшей вероятностью сплю в данный момент времени. Аналогично, график смещается влево, если мой свет выключен. Понять смысл теоремы Байеса непросто, но эта иллюстрация наглядно демонстрирует, зачем ее нужно использовать. Формула Байеса — инструмент для уточнения прогнозов с помощью дополнительных данных.

Что, если есть еще больше данных?

Зачем останавливаться на освещении в спальне? Мы можем использовать еще больше данных в нашей модели для дальнейшего уточнения оценки (пока данные остаются полезными для рассматриваемого случая). Например, я знаю, что если мой телефон заряжается, то я сплю с вероятностью 95%. Этот факт можно учесть в нашей модели.

Предположим, что вероятность того, что мой телефон заряжается, не зависит от освещения в спальне (независимость событий — это достаточно сильное упрощение, но оно позволит сильно облегчить задачу). Составим новое, еще более точное выражение для вероятности:

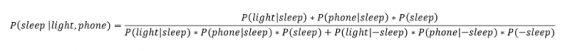
Получившаяся формула выглядит громоздко, но, используя код на Python, мы можем написать функцию, которая будет производить расчет. Для любого момента времени и любой комбинации наличия освещения/зарядки телефона эта функция возвращает уточненную вероятность того, что я сплю.

Пропустим математику (все равно считать будет компьютер) и перейдем к результатам:

Time is 11:00:00           PM Light is ON           Phone IS NOT charging.

The prior probability of sleep: 95.52%
The updated probability of sleep: 1.74%

В 23:00 без дополнительной информации мы могли почти с полной вероятностью сказать, что я сплю. Однако, как только у нас будет дополнительная информация о том, что свет включен, а телефон не заряжается, мы заключаем, что вероятность того, что я сплю, практически равна нулю. Вот еще один пример:

Time is 10:15:00 PM           Light is OFF           Phone IS charging.

The prior probability of sleep: 50.79%
The updated probability of sleep: 95.10%

Вероятность смещается вниз или вверх в зависимости от конкретной ситуации. Чтобы продемонстрировать это, рассмотрим четыре конфигурации дополнительных данных и то, как они изменяют распределение вероятности:

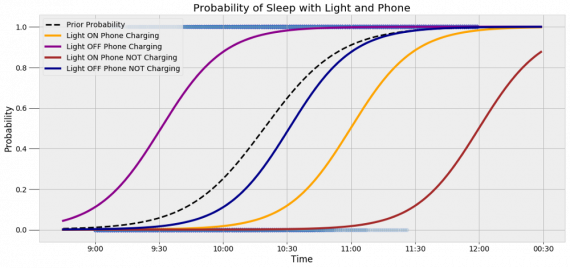
На этом графике представлено много информации, но главный смысл состоит в том, что кривая вероятности изменяется в зависимости от дополнительных факторов. По мере добавления других данных мы будем  получать более точную оценку.

Заключение

Теорема Байеса и другие статистические понятия могут быть трудными для понимания, когда они представлены абстрактными уравнениями, использующими только буквы или выдуманные ситуации. Настоящее обучение приходит, когда мы применяем абстрактные понятия в реальных задачах.

Успех в области data science — это непрерывное обучение, добавление новых методов в набор навыков и поиск оптимального метода для решения задач. Теорема Байеса позволяет уточнять наши оценки вероятности с помощью дополнительной информации для более качественного моделирования реальности. Увеличение количества информации позволяет получать более точные прогнозы, и метод Байеса оказывается полезным инструментом для решения этой задачи.

Я приветствую обратную связь, дискуссию и конструктивную критику. Связаться со мной можно в Twitter: @koehrsen_will.

Оригинал

Может быть интересно:

• Недавно ученые смоделировали поведение религиозных групп, и предсказали вероятность этнического конфликта европейцев с беженцами с Ближнего востока.
• Как работать с векторными представлениями слов;
• Как работает нейронная сеть — алгоримы, обучение, активация