Джеймс Лой, Технологический университет штата Джорджия. Руководство для новичков, после которого вы сможете создать собственную нейронную сеть на Python.
Мотивация: ориентируясь на личный опыт в изучении глубокого обучения, я решил создать нейронную сеть с нуля без сложной учебной библиотеки, такой как, например, TensorFlow. Я считаю, что для начинающего Data Scientist-а важно понимание внутренней структуры нейронной сети.
Эта статья содержит то, что я усвоил, и, надеюсь, она будет полезна и для вас! Другие полезные статьи по теме:
- Обучение с подкреплением на Python с библиотекой Keras
- Пример решения задачи по машинному обучению на Python
Что такое нейронная сеть?
Большинство статей по нейронным сетям при их описании проводят параллели с мозгом. Мне проще описать нейронные сети как математическую функцию, которая отображает заданный вход в желаемый результат, не вникая в подробности.
Нейронные сети состоят из следующих компонентов:
- входной слой, x
- произвольное количество скрытых слоев
- выходной слой, ŷ
- набор весов и смещений между каждым слоем W и b
- выбор функции активации для каждого скрытого слоя σ; в этой работе мы будем использовать функцию активации Sigmoid
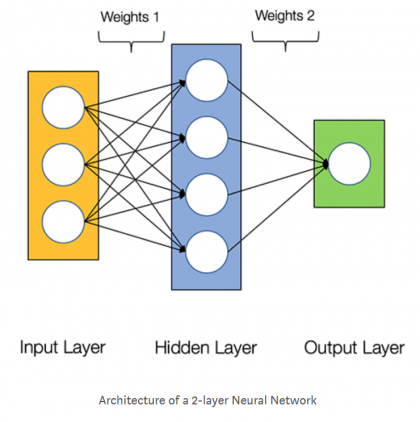
На приведенной ниже диаграмме показана архитектура двухслойной нейронной сети (обратите внимание, что входной уровень обычно исключается при подсчете количества слоев в нейронной сети).
Создание класса Neural Network на Python выглядит просто:
Обучение нейронной сети
Выход ŷ простой двухслойной нейронной сети:
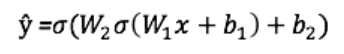
В приведенном выше уравнении, веса W и смещения b являются единственными переменными, которые влияют на выход ŷ.
Естественно, правильные значения для весов и смещений определяют точность предсказаний. Процесс тонкой настройки весов и смещений из входных данных известен как обучение нейронной сети.
Каждая итерация обучающего процесса состоит из следующих шагов
- вычисление прогнозируемого выхода ŷ, называемого прямым распространением
- обновление весов и смещений, называемых обратным распространением
Последовательный график ниже иллюстрирует процесс:
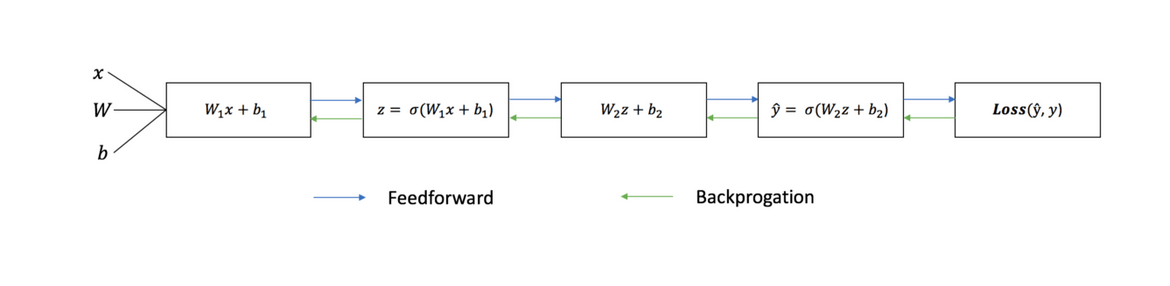

Прямое распространение
Как мы видели на графике выше, прямое распространение — это просто несложное вычисление, а для базовой 2-слойной нейронной сети вывод нейронной сети дается формулой:
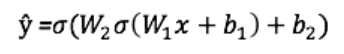
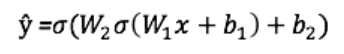
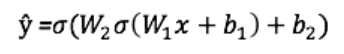
Давайте добавим функцию прямого распространения в наш код на Python-е, чтобы сделать это. Заметим, что для простоты, мы предположили, что смещения равны 0.
Однако нужен способ оценить «добротность» наших прогнозов, то есть насколько далеки наши прогнозы). Функция потери как раз позволяет нам сделать это.
Функция потери
Есть много доступных функций потерь, и характер нашей проблемы должен диктовать нам выбор функции потери. В этой работе мы будем использовать сумму квадратов ошибок в качестве функции потери.


Сумма квадратов ошибок — это среднее значение разницы между каждым прогнозируемым и фактическим значением.
Цель обучения — найти набор весов и смещений, который минимизирует функцию потери.
Обратное распространение
Теперь, когда мы измерили ошибку нашего прогноза (потери), нам нужно найти способ распространения ошибки обратно и обновить наши веса и смещения.
Чтобы узнать подходящую сумму для корректировки весов и смещений, нам нужно знать производную функции потери по отношению к весам и смещениям.
Напомним из анализа, что производная функции — это тангенс угла наклона функции.
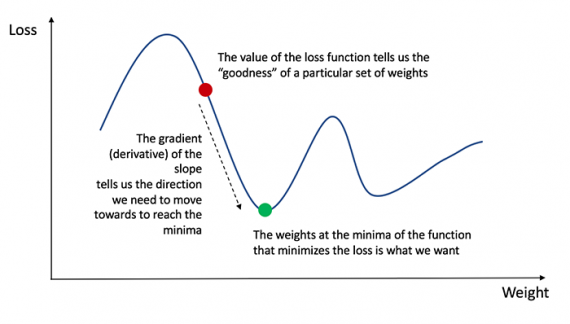

Если у нас есть производная, то мы можем просто обновить веса и смещения, увеличив/уменьшив их (см. диаграмму выше). Это называется градиентным спуском.
Однако мы не можем непосредственно вычислить производную функции потерь по отношению к весам и смещениям, так как уравнение функции потерь не содержит весов и смещений. Поэтому нам нужно правило цепи для помощи в вычислении.
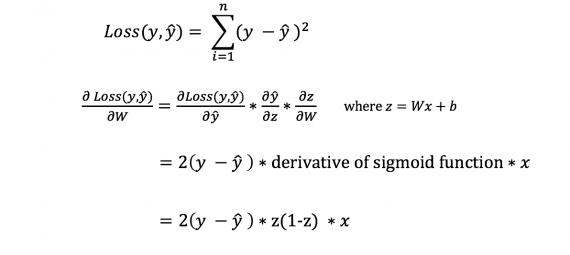
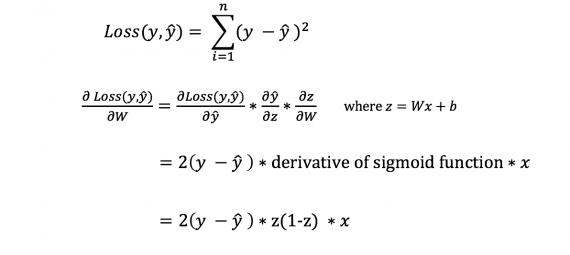
Фух! Это было громоздко, но позволило получить то, что нам нужно — производную (наклон) функции потерь по отношению к весам. Теперь мы можем соответствующим образом регулировать веса.
Добавим функцию backpropagation (обратного распространения) в наш код на Python-е:
Проверка работы нейросети
Теперь, когда у нас есть наш полный код на Python-е для выполнения прямого и обратного распространения, давайте рассмотрим нашу нейронную сеть на примере и посмотрим, как это работает.
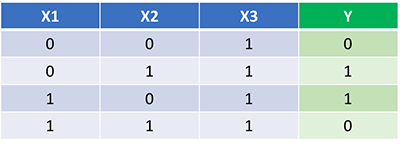

Наша нейронная сеть должна изучить идеальный набор весов для представления этой функции.
Давайте тренируем нейронную сеть на 1500 итераций и посмотрим, что произойдет. Рассматривая график потерь на итерации ниже, мы можем ясно видеть, что потеря монотонно уменьшается до минимума. Это согласуется с алгоритмом спуска градиента, о котором мы говорили ранее.
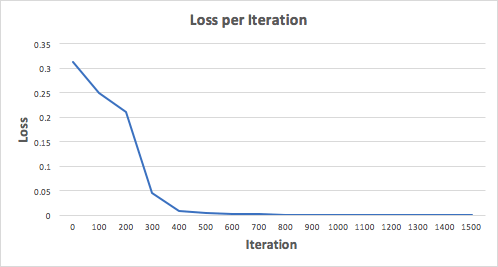

Посмотрим на окончательное предсказание (вывод) из нейронной сети после 1500 итераций.
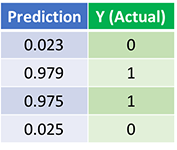

Мы сделали это! Наш алгоритм прямого и обратного распространения показал успешную работу нейронной сети, а предсказания сходятся на истинных значениях.
Заметим, что есть небольшая разница между предсказаниями и фактическими значениями. Это желательно, поскольку предотвращает переобучение и позволяет нейронной сети лучше обобщать невидимые данные.
Финальные размышления
Я многому научился в процессе написания с нуля своей собственной нейронной сети. Хотя библиотеки глубинного обучения, такие как TensorFlow и Keras, допускают создание глубоких сетей без полного понимания внутренней работы нейронной сети, я нахожу, что начинающим Data Scientist-ам полезно получить более глубокое их понимание.
Я инвестировал много своего личного времени в данную работу, и я надеюсь, что она будет полезной для вас!