Градиентный спуск: всё, что нужно знать

Градиентный спуск — самый используемый алгоритм обучения нейронных сетей, он применяется почти в каждой модели машинного обучения. Метод градиентного спуска с некоторой модификацией широко используется для обучения персептрона и глубоких нейронных сетей, и известен как метод обратного распространения ошибки.

В этом посте вы найдете объяснение градиентного спуска с небольшим количеством математики. Краткое содержание:

• Смысл ГС — объяснение всего алгоритма;
• Различные вариации алгоритма;
• Реализация кода: написание кода на языке Python.

Что такое градиентный спуск

Градиентный спуск — метод нахождения минимального значения функции потерь (существует множество видов этой функции). Минимизация любой функции означает поиск самой глубокой впадины в этой функции. Имейте в виду, что функция используется, чтобы контролировать ошибку в прогнозах модели машинного обучения. Поиск минимума означает получение наименьшей возможной ошибки или повышение точности модели. Мы увеличиваем точность, перебирая набор учебных данных при настройке параметров нашей модели (весов и смещений).

Итак, градиентный спуск нужен для минимизации функции потерь.

Суть алгоритма – процесс получения наименьшего значения ошибки. Аналогично это можно рассматривать как спуск во впадину в попытке найти золото на дне ущелья (самое низкое значение ошибки).

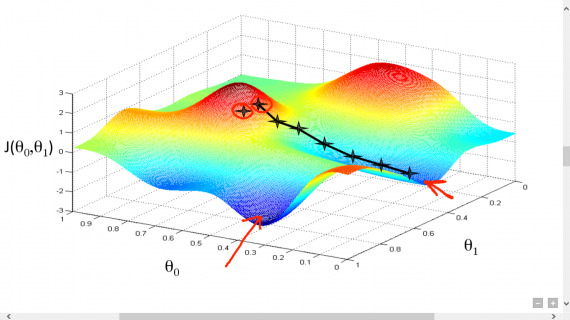
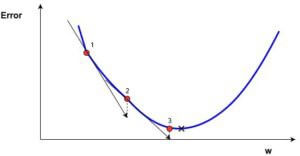
В дальнейшем, чтобы найти самую низкую ошибку (глубочайшую впадину) в функции потерь (по отношению к одному весу), нужно настроить параметры модели. Как мы их настраиваем? В этом поможет математический анализ. Благодаря анализу мы знаем, что наклон графика функции – производная от функции по переменной. Это наклон всегда указывает на ближайшую впадину!

На рисунке мы видим график функции потерь (названный «Ошибка» с символом «J») с одним весом. Теперь, если мы вычислим наклон (обозначим это dJ/dw) функции потерь относительно одного веса, то получим направление, в котором нужно двигаться, чтобы достичь локальных минимумов. Давайте пока представим, что наша модель имеет только один вес.

Важно: когда мы перебираем все учебные данные, мы продолжаем добавлять значения  dJ/dw для каждого веса. Так как потери зависят от примера обучения, dJ/dw также продолжает меняться. Затем делим собранные значения на количество примеров обучения для получения среднего. Потом мы используем это среднее значение (каждого веса) для настройки каждого веса.

Также обратите внимание: Функция потерь предназначена для отслеживания ошибки с каждым примером обучениям, в то время как производная функции относительного одного веса – это то, куда нужно сместить вес, чтобы минимизировать ее для этого примера обучения. Вы можете создавать модели даже без применения функции потерь. Но вам придется использовать производную относительно каждого веса (dJ/dw).

Теперь, когда мы определили направление, в котором нужно подтолкнуть вес, нам нужно понять, как это сделать. Тут мы используем коэффициент скорости обучения, его называют гипер-параметром. Гипер-параметр – значение, требуемое вашей моделью, о котором мы действительно имеем очень смутное представление. Обычно эти значения могут быть изучены методом проб и ошибок. Здесь не так: одно подходит для всех гипер-параметров. Коэффициент скорости обучения можно рассматривать как «шаг в правильном направлении», где направление происходит от dJ/dw.

Это была функция потерь построенная на один вес. В реальной модели мы делаем всё перечисленное выше для всех весов, перебирая все примеры обучения. Даже в относительно небольшой модели машинного обучения у вас будет более чем 1 или 2 веса. Это затрудняет визуализацию, поскольку график будет обладать размерами, которые разум не может себе представить.

Подробнее о градиентах

Кроме функции потерь градиентный спуск также требует градиент, который является dJ/dw (производная функции потерь относительно одного веса, выполненная для всех весов). dJ/dw зависит от вашего выбора функции потерь. Наиболее распространена функция потерь среднеквадратичной ошибки.

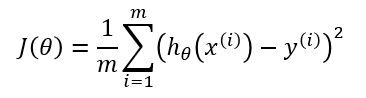
Производная этой функции относительно любого веса (эта формула показывает вычисление градиента для линейной регрессии):

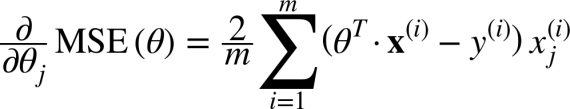
Это – вся математика в ГС. Глядя на это можно сказать, что по сути, ГС не содержит много математики. Единственная математика, которую он содержит  в себе – умножение и деление, до которых мы доберемся. Это означает, что ваш выбор функции повлияет на вычисление градиента каждого веса.

Коэффициент скорости обучения

Всё, о чём написано выше, есть в учебнике. Вы можете открыть любую книгу о градиентном спуске, там будет написано то же самое. Формулы градиентов для каждой функции потерь можно найти в интернете, не зная как вывести их самостоятельно.

Однако проблема у большинства моделей возникает с коэффициентом скорости обучения. Давайте взглянем на обновленное выражение для каждого веса (j лежит в диапазоне от 0 до количества весов, а Theta-j это j-й вес в векторе весов, k лежит в диапазоне от 0 до количества смещений, где B-k — это k-е смещение в векторе смещений). Здесь alpha – коэффициент скорости обучения. Из этого можно сказать, что мы вычисляем dJ/dTheta-j ( градиент веса Theta-j), и затем шаг размера alpha в этом направлении. Следовательно, мы спускаемся по градиенту. Чтобы обновить смещение, замените Theta-j на B-k.

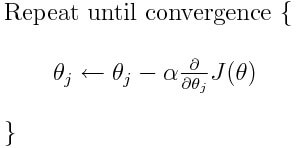
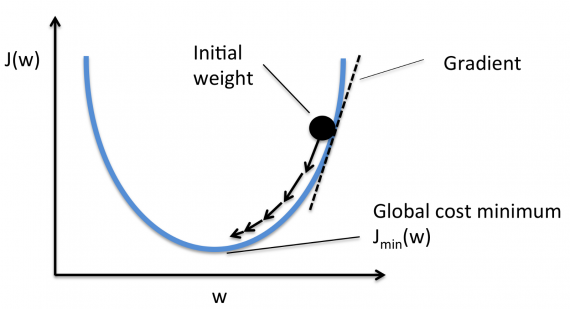
Если этот размера шага alpha слишком велик, мы преодолеем минимум: то есть промахнемся мимо минимума. Если alpha слишком мала, мы используем слишком много итераций, чтобы добраться до минимума. Итак, alpha должна быть подходящей.

Использование градиентного спуска

Что ж, вот и всё. Это всё, что нужно знать про градиентный спуск. Давайте подытожим всё в псевдокоде.

Примечание: Весы здесь представлены в векторах. В более крупных моделях они, наверное, будут матрицами.

От i = 0 до «количество примеров обучения»

1. Вычислите градиент функции потерь для i-го примера обучения по каждому весу и смещению. Теперь у вас есть вектор, который полон градиентами для каждого веса и переменной, содержащей градиент смещения.

2. Добавьте градиенты весов, вычисленные для отдельного аккумулятивного вектора, который после того, как вы выполнили итерацию по каждому учебному примеру, должен содержать сумму градиентов каждого веса за несколько итераций.

3. Подобно ситуации с весами, добавьте градиент смещения к аккумулятивной переменной.

Теперь, ПОСЛЕ перебирания всех примеров обучения, выполните следующие действия:

1. Поделите аккумулятивные переменные весов и смещения на количество примеров обучения. Это даст нам средние градиенты для всех весов и средний градиент для смещения. Будем называть их обновленными аккумуляторами (ОА).

2. Затем, используя приведенную ниже формулу, обновите все веса и смещение. Вместо dJ / dTheta-j вы будете подставлять ОА (обновленный аккумулятор) для весов и ОА для смещения. Проделайте то же самое для смещения.

Это была только одна итерация градиентного спуска.

Повторите этот процесс от начала до конца для некоторого количества итераций. Это означает, что для 1-й итерации ГС вы перебираете все примеры обучения, вычисляете градиенты, потом обновляете веса и смещения.  Затем вы проделываете это для некоторого количества итераций ГС.

Различные типы градиентного спуска

Существует 3 варианта градиентного спуска:

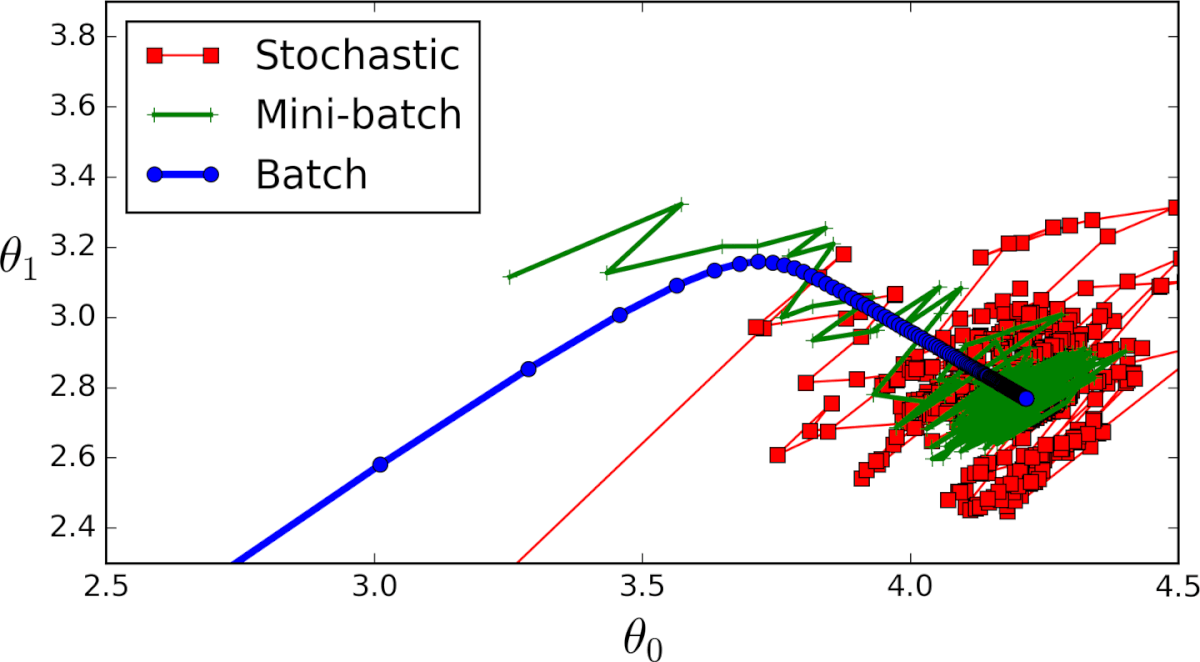
1. Мini-batch: тут, вместо поочерёдного перебора всех примеров обучения и произведения необходимых вычислений для каждого из них, мы производим вычисления для n примеров обучения сразу. Этот выбор подходит для очень больших наборов данных.

2. Стохастический градиентный спуск: в этом случае вместо перебора и использования всего набора примеров обучения мы применяем подход “используй только один”. Здесь нужно отметить несколько моментов:

• Набор примеров обучения необходимо перемешать перед каждым его проходом в ГС, чтобы перебирать их каждый раз в случайном порядке.
• Поскольку каждый раз используется только один пример обучения, то ваш путь к локальному минимуму будет очень неоптимальным;
• С каждой итерацией ГС вам нужно перемешать набор обучения и выбрать случайный пример обучения;
• Поскольку вы используете только один пример обучения, ваш путь к локальным минимумам будет очень шумным.

3. Серия ГС: это то, о чем написано в предыдущих разделах. Цикл на каждом примере обучения.

Пример кода на python

Применимо к cерии ГС, так будет выглядеть блок учебного кода на Python.

def train(X, y, W, B, alpha, max_iters):
'''
Performs GD on all training examples,
X: Training data set,
y: Labels for training data,
W: Weights vector,
B: Bias variable,
alpha: The learning rate,
max_iters: Maximum GD iterations.
'''
dW = 0 # Weights gradient accumulator
dB = 0 # Bias gradient accumulator
m = X.shape[0] # No. of training examples
for i in range(max_iters):
dW = 0 # Reseting the accumulators
dB = 0
for j in range(m):
# 1. Iterate over all examples,
# 2. Compute gradients of the weights and biases in w_grad and b_grad,
# 3. Update dW by adding w_grad and dB by adding b_grad,
W = W - alpha * (dW / m) # Update the weights
B = B - alpha * (dB / m) # Update the bias return W, B # Return the updated weights and bias.

Вот и всё. Теперь вы должны хорошо понимать, что такое метод градиентного спуска.