Капсульная нейронная сеть или CapsNet

Сверточные сети сделали потрясающую работу, но завязли в проблемах. Настало время начать думать о новых решениях или улучшениях. Эта статья — введение в капсульные нейронные сети. После прочтения вы поймете, как работают CapsNet и в чем их приципиальное отличие.

Чтобы легче воспринимать материал и следовать статье, я подготовил инструмент визуализации, который позволит вам увидеть происходящее в каждом слое. В паре с визуализацией идет простая реализация сети. Все это вы можете найти в этом репозитории на GitHub.

Ниже представлена архитектура сети CapsNet. Не беспокойтесь, если вы не понимаете, что здесь представлено. Я расскажу про каждую деталь настолько много, насколько это возможно, проходя слой за слоем.

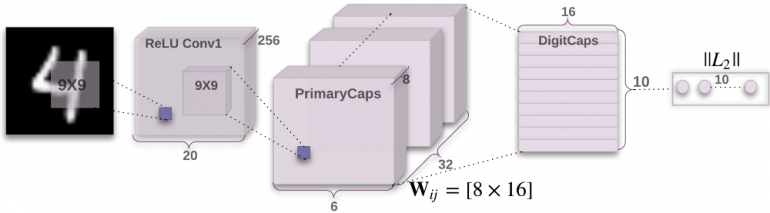
Часть 0: Вход

На вход нейронной сети CapsNet подается изображение. В этом примере входное изображение имеет размер 28 пикселей в высоту и 28 в ширину. Но в действительности, изображения находятся в трехмерном пространстве, где третье пространство содержит цветовые каналы.

Изображение в нашем примере имеет только один канал, так как оно черно-белое. Большинство известных вам изображений имеют 3 или 4 канала: RGB и, возможно, дополнительный канал альфа, отвечающий за прозрачность.

Каждый из этих пикселей представлен как число в диапазоне от 0 до 255 и хранится в матрице размера [28, 28, 1]. Чем светлее пиксель, тем больше его значение.

Часть 1а: Свертка

Первая часть CapsNet — традиционный сверточный слой. Возникают вопросы:

• Что такое сверточный слой?
• Как он работает?
• Зачем он вообще нужен?

Цель состоит в извлечении из входного изображения самых базовых признаков — грани или кривые.

Как можно это сделать? Посмотрим на грань:

Если посмотреть на несколько точек на изображении, можно начать улавливать паттерн. Возьмем цвета слева и справа от выбранной точки:

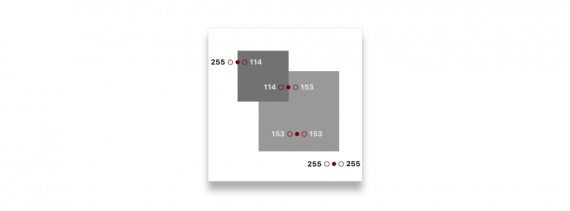
Можно заметить большую разницу в случае, если выбранная точка — грань:

255 - 114 = 141
114 - 153 = -39
153 - 153 = 0
255 - 255 = 0

Что будет, если мы пройдем по всем пикселям изображения и заменим их значения на значения разности между левым и правым пикселем? В теории изображение должно целиком стать черным за исключением граней.

Мы можем реализовать такую операцию с помощью цикла, проходя по каждому пикселю изображения:

for pixel in image {
result[pixel] = image[pixel - 1] - image[pixel + 1]
}

Но такой способ не самый эффективный. Вместо этого разумнее использовать свертку. Говоря техническим языком, это взаимная корреляция, но все любят называть эту операцию сверткой.

Свертка по сути делает тоже самое, что и цикл, но получает преимущества за счет матричной математики. Операция свертки выполняется за счет встраивания маленького окна в углу изображения, которое позволяет видеть только пиксели в этой области. Затем окно перемещается через все пиксели изображения, умножая каждый пиксель на набор весов и складывая все значения в этом окне.

Окно представляет собой матрицу весов, называемую кернелом (kernel, ядро).

Нас волнуют только 2 пикселя, но когда мы направляем окно вокруг них, оно инкапсулирует пиксель между ними.

Window:
┌─────────────────────────────────────┐
│ left_pixel middle_pixel right_pixel │
└─────────────────────────────────────┘

Можете ли вы представить себе такой набор весов, на который умножаются эти пиксели, чтобы получившаяся сумма складывалась в ожидаемое значение?

Window:
┌─────────────────────────────────────┐
│ left_pixel middle_pixel right_pixel │
└─────────────────────────────────────┘
(w1 * 255) + (w2 * 255) + (w3 * 114) = 141

Можно сделать, например, так:

Window:
┌─────────────────────────────────────┐
│ left_pixel middle_pixel right_pixel │
└─────────────────────────────────────┘
(1 * 255) + (0 * 255) + (-1 * 114) = 141

С этими весами кернел будет выглядеть следующим образом:

kernel = [1 0 -1]

Однако, кернелы обычно квадратные. Можем просто заполнить пустые места нулями вот так:

kernel = [
[0 0 0]
[1 0 -1]
[0 0 0]
]

Анимация помогает разобраться в процессе:

Отметим: размерность выхода уменьшается на размер кернела и добавляется 1. Например: (7-3) + 1 = 5 (подробнее об этом речь пойдет ниже).

Вот так будет выглядеть оригинальное изображение после действия на него свертки с нашим кернелом:

Вы можете заметить, что пропала пара граней. Более точно, пропали горизонтальные грани. Чтобы решить эту проблему, необходимо добавить другой кернел, который смотрит на верхний и нижний пиксели указанной точки. Такой кернел может выглядеть:

kernel = [
[0 1 0]
[0 0 0]
[0 -1 0]
]

Стоит сказать, что оба этих кернела не будут хорошо работать с размытыми гранями или расположенными под другими углами. По этой причине используется много кернелов (в нашей реализации CapsNet кернелов 256 штук). Для достижения большей гибкости операции кернелы обычно делаются больше чем 3х3 (наши кернелы будут иметь размер 9х9).

Так выглядит один из кернелов после тренировки модели. Может быть не совсем очевидно, но это просто увеличенная версия нашего детектора граней. В таком виде детектор более надежный и способен находить и светлые и темные грани.

kernel = [
[ 0.02 -0.01 0.01 -0.05 -0.08 -0.14 -0.16 -0.22 -0.02]
[ 0.01 0.02 0.03 0.02 0.00 -0.06 -0.14 -0.28 0.03]
[ 0.03 0.01 0.02 0.01 0.03 0.01 -0.11 -0.22 -0.08]
[ 0.03 -0.01 -0.02 0.01 0.04 0.07 -0.11 -0.24 -0.05]
[-0.01 -0.02 -0.02 0.01 0.06 0.12 -0.13 -0.31 0.04]
[-0.05 -0.02 0.00 0.05 0.08 0.14 -0.17 -0.29 0.08]
[-0.06 0.02 0.00 0.07 0.07 0.04 -0.18 -0.10 0.05]
[-0.06 0.01 0.04 0.05 0.03 -0.01 -0.10 -0.07 0.00]
[-0.04 0.00 0.04 0.05 0.02 -0.04 -0.02 -0.05 0.04]
]

Отметим: значения матрицы кернела округлены, так как они слишком длинные. Например: 0.01783941

Нам не надо вручную выбирать кернелы. За нас это сделает тренировочный код. В самом начале все кернелы пустые (или имеют случайные значения) и в процессе обучения они постепенно изменяются, чтобы сделать выход ближе к тому, что мы хотим.

Вот так в конечном итоге выглядят 256 кернелов (для лучшего усвоения я раскрасил их как пиксели), где размер каждого кернела 9х9. Чем меньше число, тем оно голубее. 0 — зеленый цвет, положительное число — желтый:

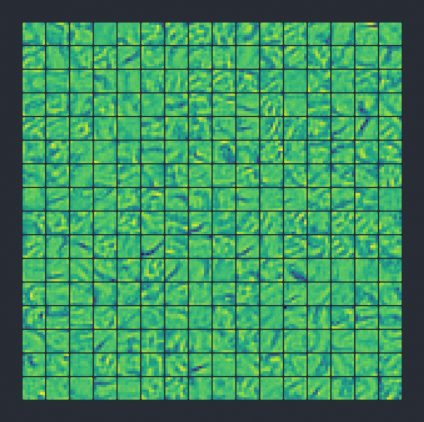
После фильтрации изображения всеми этими кернелами мы получим набор из 256 выходных изображений.

Часть 2б: ReLU

ReLU (формально известный как линейный выпрямитель) достаточно простая вещь. Это активационная функция, аргументом которой является значение. Если это значение отрицательно, ReLU зануляется, если положительное — принимает значение аргумента.

То есть:

x = max(0, x)

Графически ReLU выглядит так:

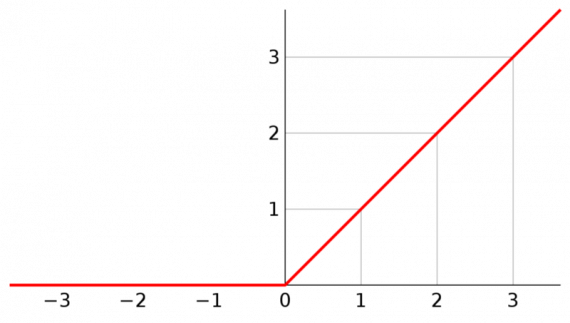
Мы применяем эту функцию ко всем выходам наших сверток.

Зачем мы это делаем? Если мы не будем применять никакую функцию активации к выходу слоя, тогда вся нейронная сеть может быть описана линейной функцией. В таком случае всё что мы здесь делаем бессмысленно.

Добавление нелинейности позволяет описывать все виды функций. Существует большое количество типов активационных функций, которые можно применить в сети. Среди этого множества ReLU — самая популярная функция, так как проста в вычислении.

Так выглядит выход из сверточного слоя Conv1 (256 выходов размером 20х20 пикселей) после применения ReLU:

Часть 2а: PrimaryCaps

Слой PrimaryCaps начинает как обычный сверточный слой, но в этот раз проводится свертывание по стеку из 256 выходов из предыдущих сверток. Вместо кернела 9х9 имеем кернел размера 9х9х256.

Что именно мы ищем? В первом сверточном слое мы искали простые грани и кривые. Сейчас же нам интересны более сложные формы, состоящие из ранее найденных граней.

Теперь шаг равен 2. Это означает, что вместо перемещения на 1 пиксель, кернел каждый раз перемещается на 2. Больший шаг был выбран, чтобы обрабатывать входные данные быстрее:

Отметим: в обычном случае размерность выхода равна 12. Но мы должны разделить это число на 2 из-за шага. Например, ((20 — 9) + 1) / 2 = 6

Будем производить свертку по выходам еще 256 раз. Результатом этого шага должен стать набор из 256х6х6 выходов.

Теперь мы нарежем стек на 32 колоды по 8 карт в каждой. Будем называть каждую колоду капсульным слоем. Каждый такой слой имеет 36 капсул.

Если вы не отстаете от меня (и являетесь гением математики), то понимаете, что каждая капсула — массив из 8 значений. Можем называть этот массив вектором.

Для лучшего понимания я показал это так:

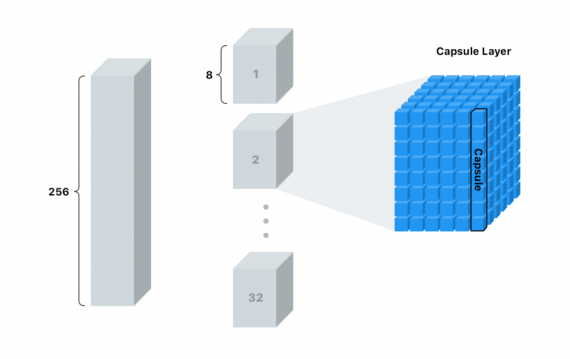
Капсулы — наши новые пиксели.

Используя один пиксель, мы можем быть уверены только в том, нашли ли мы грань в этой области или нет. Чем больше число, тем больше эта уверенность.

В капсуле мы можем хранить 8 значений для данной локации! Это дает возможность хранить больше информации, чем просто знание о наличии или отсутствии формы в этом месте. Но какую еще информацию можно хранить?

Смотря на фигуру ниже, что вы можете сказать о ней? Если бы вам пришлось объяснить человеку, ни разу не видевшему эту фигуру, как её нарисовать, чтобы вы сказали?

Хотя это изображение очень простое, отметим несколько деталей, требуемых для описания фигуры:

• Тип фигуры
• Положение
• Ориентация
• Цвет
• Размер

Для конкретизации можно назвать эти параметры. Чем сложнее изображения, тем больше деталей необходимо указывать. Этими параметрами могут быть: расположение, размер, ориентация, деформация, альбедо, оттенок, текстура и тому подобное.

Вы наверное помните, что наш кернел для детектирования граней работает только под определенным углом. Поэтому требуется кернел для каждого угла. Мы бы могли избежать неприятностей при работе с гранями, так как существует очень мало способов их описания. Когда мы поднимаемся на уровень фигур, нет желания делать кернел для каждого угла прямоугольника, овала, треугольника и прочих. Это было бы слишком затратно, и ситуация осложнялась бы при работе с более сложными фигурами, которые имеют трехмерные вращения и признаки, такие как освещенность.

Это еще одна из причин, почему традиционные нейронные сети плохо справляются с вращениями:

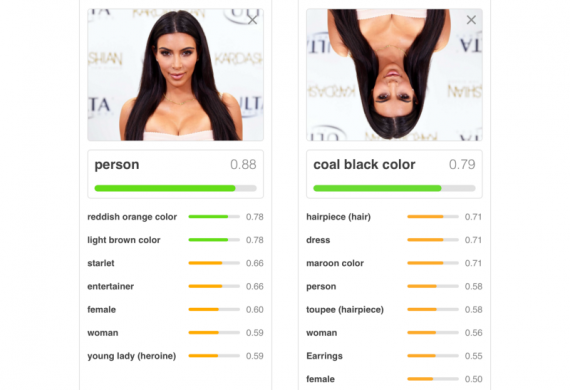
Поскольку мы уходим от граней к фигурам, а от фигур к объектам, неплохо иметь больше пространства для хранения дополнительной полезной информации.

Ниже представлено упрощенное сравнение выходов 2 капсульных слоев (один для прямоугольников, другой для треугольников) против 2 традиционных пикселей:

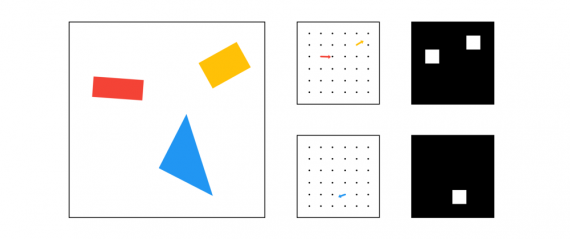
Также как в традиционных двумерных или трехмерных векторах, этот вектор имеет угол и длину. Длина описывает вероятность, а угол — вспомогательные параметры. В примере, показанном сверху, угол действительно соответствует углу фигуры, но такое бывает не всегда.

На практике не удается (или это сделать не просто) визуализировать вектор, как это сделано сверху, так как такие вектора в 8-мерном пространстве.

Так как в капсуле находится вся дополнительная информация, можно попытаться пересоздать изображение.

Звучит неплохо, но как уговорить сеть начать изучать эти штуки?

Тренируя традиционную сверточную сеть, нас заботит только правильность предсказания модели. В капсульной сети появляется новый прием — реконструкция. Реконструкция берет созданный вектор и пытается воссоздать оригинальное изображение только по этому вектору. Далее происходит оценка модели на основе того, насколько точно изображение после реконструкции совпадает с оригинальным изображением.

Я более подробно опишу этот процесс в следующем разделе, а пока покажу простой пример:

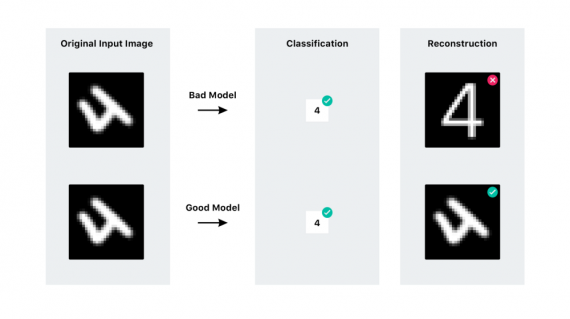
Часть 2б: Сжатие

Теперь у нас есть капсулы и есть необходимость использовать еще одну нелинейную функцию на них (можно ReLU). Только в этот раз уравнение немного сложнее. Функция преобразует значения вектора таким образом, что меняется только его длина, а углы остаются постоянными. Таким получается вектор в диапазоне от 0 до 1, что соответствует вероятности.

Так выглядит длина капсульного вектора после сжатия. На этом моменте уже практически невозможно определить, на что каждая капсула обращает внимание.

Обратите внимание, что каждый пиксель теперь является вектором длины 8

Часть 3: Направление по соглашению

Следующий шаг — решить, какую информацию отправить в следующий слой. В традиционных сетях мы бы использовали операцию max pooling. Это отличный способ уменьшить размер при помощи отправления в следующий слой только пикселя с максимальным значением в выбранной области.

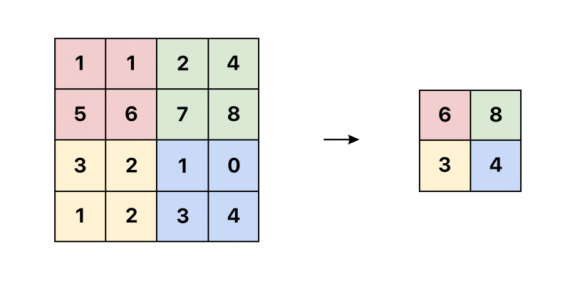
Однако в капсульных сетях мы собираемся реализовать другой метод — направление по соглашению (routing by agreement). Лучший пример такого метода — пример с лодкой и домом, показанный Aurélien Géron в этом замечательном видео. Каждая капсула, основываясь на самой себе, пытается предсказать активацию следующего слоя:

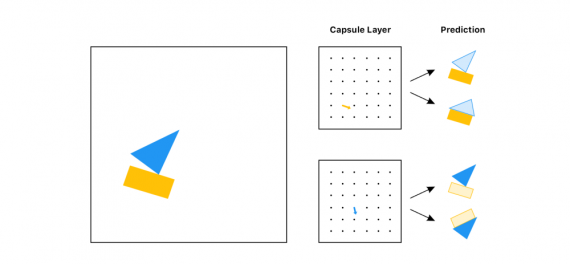
Смотря на эти предсказания, какой бы объект вы передали в следующий слой (не зная входа)?  Лодку, правильно? И прямоугольная и треугольная капсулы сходятся во мнении, как будет выглядеть лодка. Но не могут прийти к единому мнению, как будет выглядеть дом, поэтому вряд ли объект является домом.

С routing by agreement мы передаем только полезную информацию, а плохие данные, которые добавляют шум в результат, выбрасываем. Так мы выполняем отбор значений умнее, чем просто выбор наибольшего значения, как делает max pooling.

В традиционных нейросетях, перепутанные элементы нас не беспокоят:

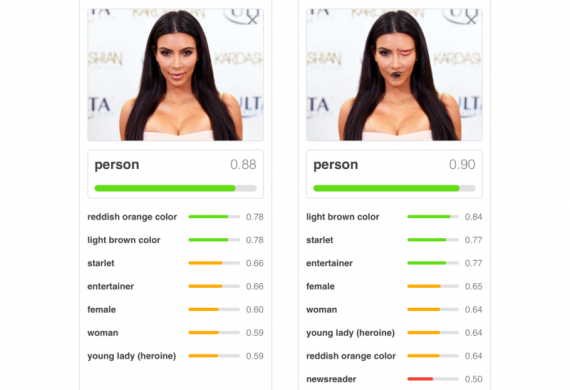
В капсульных сетях такие признаки не будут согласовываться друг с другом:

Надеюсь, у вас появилось интуитивное представление. Что насчет математики этой модели?

Имеем 10 различных классов символов, которые хотим предсказать:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Отметим: в примере с домом и лодкой предсказывались 2 объекта, сейчас же — 10.

В отличии от примера с лодкой и домом предсказания в действительности не являются изображениями. Вместо этого пытаемся предсказать вектор, который уже описывает изображение.

Предсказание капсулы для каждого класса создается путем перемножения соответствующего вектора на матрицу весов для каждого класса, который мы пытаемся предсказать.

Вспомним, что в сети 32 капсульных слоя, в каждом из которых 36 капсул. Всего получается 1152 капсул.

cap_1 * weight_for_0 = prediction
cap_1 * weight_for_1 = prediction
cap_1 * weight_for_2 = prediction
cap_1 * ...
cap_1 * weight_for_9 = prediction
cap_2 * weight_for_0 = prediction
cap_2 * weight_for_1 = prediction
cap_2 * weight_for_2 = prediction
cap_2 * ...

В конечном итоге получаем список из 11520 предсказаний.

Каждый вес представляет собой такую матрицу 16х8, что предсказание — матричное умножение капсульного вектора и весовой матрицы:

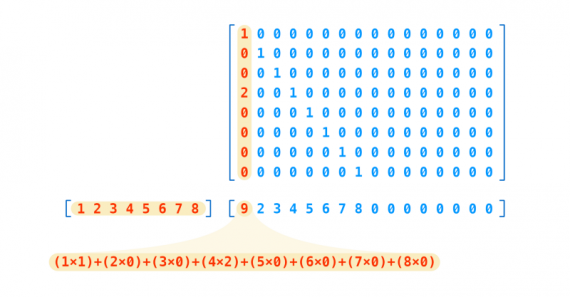
Как можно видеть, наше предсказание — вектор с 16 элементами. Откуда взялось число 16? Это произвольный выбор, также как и 8 для оригинальных капсул.

Стоит сказать, что мы хотим увеличивать число измерений наших капсул по мере продвижения внутрь сети. Это должно быть интуитивно понятно. Чем глубже мы погружаемся, тем сложнее становятся наши признаки и тем большее количество параметров нам нужно для их воссоздания. Например, необходимо больше информации для описания всего лица, чем просто для описания глаза.

Следующий шаг — определить, какие из 11520 предсказаний лучше других согласуются друг с другом.

В данном случае тяжело визуализировать решение этой задачи,так как мы работаем с векторами в многомерном пространстве. Давайте для простоты начнем с представления вектора, как точки в двумерном пространстве:

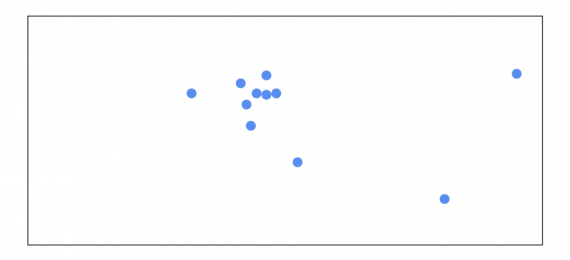
Начинаем подсчитываь среднее всех точек. В самом начале все точки имеют одинаковую важность:

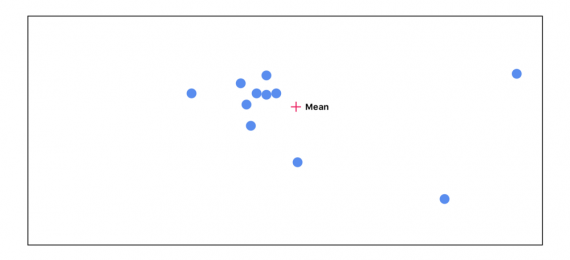
Далее считаем расстояние между каждой точкой и средним. Чем дальше расположена точка от среднего, тем менее важной она становится:

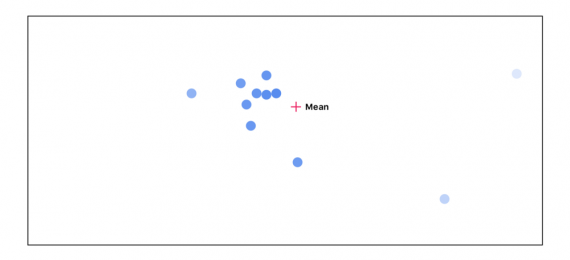
Снова пересчитываем среднее, учитывая важность каждой точки:

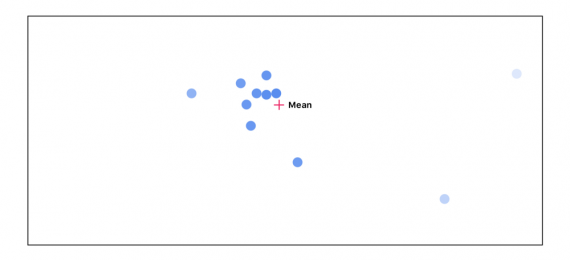
Проходим этот цикл 3 раза:

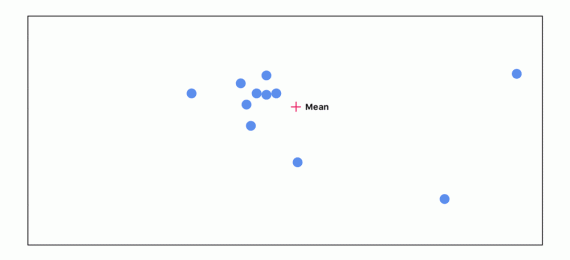
Можно видеть, по мере прохождения цикла точки, которые не согласуются с остальными, исчезают. Точки наибольшего согласия отправляются в следующий слой.

Часть 4: DigitCaps

После процедуры соглашения получаем десять 16-мерных векторов, по одному на каждый знак. Эта матрица — наше финальное предсказание. Длина вектора представляет собой уверенность в найденном знаке — чем длиннее, тем лучше. Кроме этого, вектор может быть использован для генерации реконструкции входного изображения.

Так выглядят длины векторов, если подать на вход цифру 4:

Пятый блок самый яркий, вызывает наибольшую уверенность. Вспомним, что 0 — первый класс, тогда по вектору определяется, что предсказывается цифра 4 (5 класс).

Часть 5: Реконструкция

Часть кода, реализующая реконструкцию, не представляет большого интереса. Это просто несколько полносвязных слоев. Но само по себе это занятие очень веселое. Вы можете с этим поиграть самостоятельно.

Если мы хотим воссоздать подаваемую на вход цифру 4 из её вектора, получится следующее:

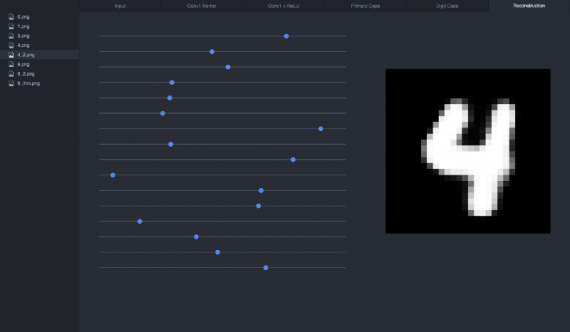
Манипулируя слайдером (меняя один из параметров вектора), можно проследить, как изменение параметра влияет на цифру 4:

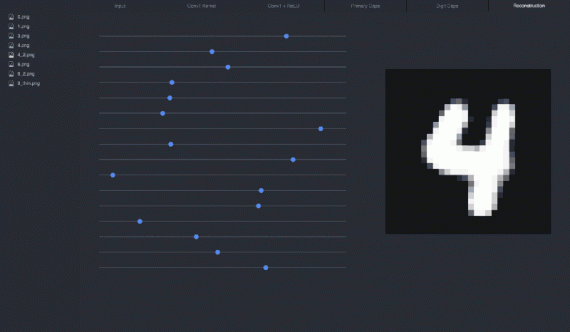
Я рекомендую скачать репозиторий с визуализацией и поиграться с параметрами, чтобы увидеть влияние их на реконструкцию:

git clone https://github.com/bourdakos1/CapsNet-Visualization.git
cd CapsNet-Visualization
pip install -r requirements.txt

Запуск инструмента:

python run_visualization.py

После этого откройте в браузере следующую ссылку: http://localhost:5000

Некоторые мысли

Думаю, реконструкции в капсульных сетях — отличный инструмент. Хотя текущая модель обучена только на простых символах, она заставляет задумываться о возможностях, которые открываются перед зрелыми архитектурами, обученными на больших датасетах.

Интересно увидеть, какой эффект будут оказывать на более сложные изображения манипуляции с реконструкционными векторами. По этой причине моим следующим проектом будет использование капсульных нейросетей для работы с датасетами CIFAR и smallNORB.