Представьте, что вы альпинист на вершине горы и наступает ночь. Вам нужно добраться до лагеря, что внизу скалы, но в свете тусклого фонарика вы можете видеть лишь на несколько метров. Так как же спуститься вниз? Одна из стратегий — оглядеться и понять, какой склон наиболее крутой, но не слишком, и сделать шаг туда. Повторить данный процесс много раз и постепенно вы доберетесь до подножья горы. Если вы застрянете в долине, это немного замедлит вас.
Обучение нейронной сети — это поиск наилучшего набора весов для максимизации точности предсказания.
Нейронные сети могут быть использованы и без четкого понимания, как именно они обучаются, так же как вы используете фонарик без четкого понимания, как работает микросхема внутри него. Современные библиотеки машинного обучения значительно автоматизируют процесс обучения нейронных сетей. Хотя обычно хочется пропустить математическую часть и поскорее приступить к практике, все же стоит внимательно прочитать об этом, так как это конвертируется в значительное преимущество при перенастройке и конфигурации сетей. Более того обучение нейросетей было описано много лет назад, но только сейчас оно стало доступным, став новой вехой в развитии DS.
Цель статьи — дать интуитивное понимание о том, как работают нейросети. Больше визуала, меньше уравнений. Поговорим о том, почему обучение нейросетей представляет сложность.
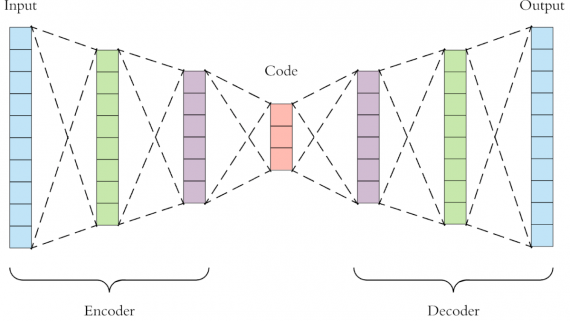
Обучение глубокой нейронной сети
Веса в скрытых слоях сильно зависимы. Чтобы понять почему, взгляните на картинку ниже, небольшое изменение веса в первом слое, окажет значительное влияние на дальнейшее распространение.

Именно поэтому мы не можем получить идеальный набор весов просто подгоняя по одному. Мы должны найти комбинацию весов сразу. Но как это сделать?
Давайте начнем с самого наивного метода: случайный перебор. Установим веса случайным образом и подсчитаем результаты. Повторить много раз, сохранить все результаты, выбрать наиболее точные. На первый взгляд это кажется не таким уж плохим подходом. И действительно, компьютеры уже очень мощные, может быть мы можем получить решение брутфорсом? Для небольших нейронок (~30 нейронов) это и вправду работает. Но для задач из реального мира, где нейронов под 12,000 , случайный перебор теряет свою актуальность. Попробуйте найти иголку в 12000-мерном стоге сена методом простого перебора.
N-мерное пространство — одинокое место
Если наша стратегия наугад найти веса, то логично задаться вопросом, сколько нужно сделать попыток для получения приемлемого набора весов. Интуитивно мы ожидаем, что сделав достаточно попыток мы покроем все пространство и найдем идеальный набор весов. Без априорных знаний веса могут быть в любой точке пространства, поэтому имеет смысл рассматривать как можно больше разных весов из пространства.
Чтобы проиллюстрировать это, давайте рассмотрим несколько простых однослойных нейросетей: с тремя и с двумя нейронами.

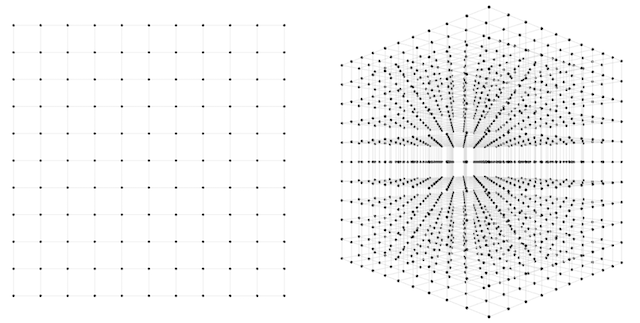
В первом случае нужно найти всего два веса. Как много попыток нужно сделать, чтобы угадать идеальный набор? Один из подходов — представить двумерное пространство возможных весов и до изнеможения искать нужную комбинацию при некотором разбиении. Возможно, мы можем разбить каждую ось на 10 частей. Тогда попыток всего будет 10^2 = 100. Не так уж и плохо, но давайте сделаем разбиение более мелким, чтобы подобрать веса корректнее, например на 100 частей. Тогда уже комбинаций может быть 10,000. Достаточно маленькое число, компьютер сможет обработать его меньше, чем за секунду.
Так, а что же со второй сетью? Теперь нам нужно подобрать уже 3 веса и, следовательно, работать в трехмерном пространстве. Проделаем такие же операции 10*10*10 = 1000 вариантов и 100*100*100 = 1,000,000 вариантов соответственно при разных вариантах разбиения. Миллион вариантов — не так уж и страшно, но рост пугающий. И что же произойдет, когда мы перейдем к реальным сеткам?
Проклятие размерности
Что же будет, когад мы попробуем классифицировать цифры из датасета MNIST? Cеть будет содержать 784 входных нейронов, 15 нейронов в 1 скрытом слое и 10 выходных нейронов. Итого 784*15 + 15*10 = 11910 весов. Получается, чтобы угадать, нужно сделать 10^11910 попыток… Это 1 почти с 12,000 нулями. Для сравнения атомов в видимой Вселенной всего 10^80. Никакой суперкомпьютер не справится с таким перебором. И эта простая сетка даже близко не сравнится с самыми современными, где десятки и тысячи миллионов весов!
В машинном обучении данная проблема носит название “проклятие размерности”. Каждое измерение, которое мы добавляем, экспоненциально увеличивает количество требуемых для обобщения образцов. Проклятие размерности чаще всего применяется к наборам данных: чем больше столбцов или переменных, тем экспоненциально больше выборок в этом датасете нам нужно проанализировать. В нашем случае мы говорим о весах, а не о входных данных, но принцип остается неизменным — многомерное пространство огромно!
Очевидно, что для решения этой проблемы должно быть более элегантное решение, чем случайные догадки. Но об этом — в следующих статьях.