Большие языковые модели хорошо справляются с математическими бенчмарками вроде AIME, однако задачи Международной математической олимпиады (IMO) требуют глубокого понимания, креативности и формального рассуждения. Китайские исследователи использовали Google Gemini 2.5 Pro на недавно опубликованных задачах IMO 2025, избегая загрязнения данных. Применив пайплайн самопроверки с тщательным дизайном промптов, они корректно решили 5 из 6 задач. Этот результат подчеркивает важность разработки оптимальных стратегий для использования полного потенциала мощных LLM в сложных задачах рассуждения.
Стратегия и методологиия решения
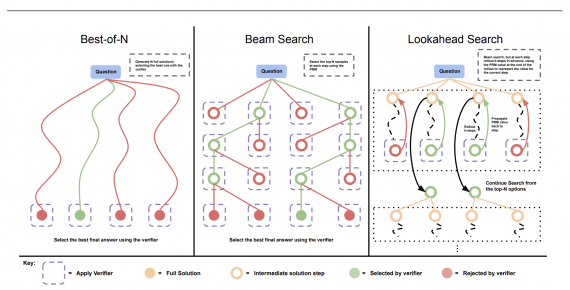
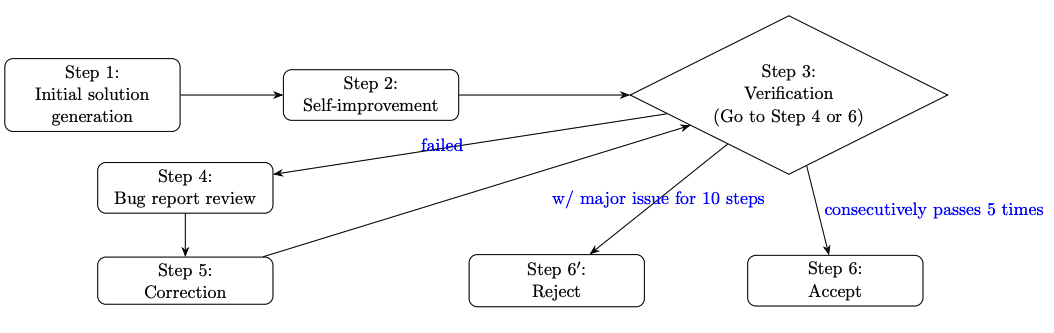
Исследователи разработали многоэтапный пайплайн для решения олимпиадных задач:
Пайплайн самопроверки включает следующие этапы:
- Генерация начального решения с акцентом на строгость;
- Самосовершенствование модели;
- Верификация решения и создание отчета об ошибках;
- Анализ отчета об ошибках;
- Исправление и улучшение решения;
- Принятие или отклонение решения.
Ключевые принципы промптинга:
- Строгость превыше всего — каждый шаг должен быть логически обоснован;
- Честность о полноте — лучше представить частичный, но строгий результат;
- Использование верстки TeX для всех математических выражений;
- Структурированный формат ответа с резюме и детальным решением.
Роль верификатора
Верификатор играет критическую роль в пайплайне, классифицируя проблемы на: критические ошибки — нарушающие логическую цепочку доказательства (логические ошибки, фактические неточности) и пробелы в обосновании — шаги, где вывод может быть корректным, но аргументация неполная или недостаточно строгая.
Система запускает верификатор пять раз на финальной стадии и принимает решение только при успешном прохождении всех проверок.
Анализ решений задач IMO 2025 моделью Gemini 2.5 Pro
Задача 1 (Комбинаторная геометрия)
Задача требовала определить все неотрицательные целые числа k для конфигураций прямых на плоскости. Gemini 2.5 Pro успешно применила математическую индукцию, сведя проблему к базовому случаю и показав, что возможными значениями являются k ∈ {0, 1, 3}.
Ключевой инсайт заключался в том, что любая конфигурация может быть сведена к случаю, когда ни одна из прямых не является «главной граничной прямой» множества точек. Через тщательный анализ ограничений на пересечения и использование свойств «солнечных» прямых (не параллельных осям x, y и прямой x+y=0), модель доказала невозможность конфигураций с k=2 или k≥4, построив при этом явные примеры для допустимых случаев.
Задача 2 (Аналитическая геометрия)
Геометрическая задача о касательности решалась методами аналитической геометрии. Модель установила систему координат и использовала алгебраические вычисления для доказательства условия касательности.
Сложность задачи заключалась в необходимости координировать взаимное расположение двух окружностей, их центров, точек пересечения и ортоцентра треугольника. Gemini 2.5 Pro методично вычислила координаты всех ключевых точек, включая центр описанной окружности треугольника ACD и ортоцентр треугольника PMN, а затем использовала условие касательности через равенство квадрата расстояния от центра окружности до прямой квадрату радиуса для завершения доказательства.
Задача 3 (Теория чисел)
Функциональное уравнение требовало найти минимальную константу c. Исследование показало, что f(1) = 1, проанализировало возможные структуры для множества простых чисел и определило c = 4.
Наиболее технически сложная часть решения включала анализ множества простых чисел Sf = {p простое | ∃n ∈ N, p | f(n)} и доказательство того, что возможны только три случая: Sf = ∅, Sf = {2}, или Sf содержит все простые числа. Через глубокий анализ сравнений по модулю и применение теоремы Дирихле о простых числах в арифметических прогрессиях, модель исключила большинство промежуточных случаев и построила максимальную функцию f₀(n), достигающую границы c = 4.
Задача 4 (Последовательности)
Анализ рекуррентной последовательности с ограничениями на собственные делители. Решение установило, что все элементы должны быть четными и делиться на 3, но не на 5, что привело к полной характеризации возможных начальных значений.
Изящность решения проявилась в систематическом доказательстве необходимых условий делимости через анализ рекуррентного соотношения an+1 = f(an), где f(N) — сумма трех наибольших собственных делителей. Модель показала, что если последовательность содержит нечетный элемент, то она становится строго убывающей и обрывается, аналогично для элементов, не делящихся на 3. Конструктивная часть доказательства включала построение явных примеров бесконечных последовательностей для каждого допустимого типа начальных значений.
Задача 5 (Теория игр)
Игра между Алисой и Баззой с различными ограничениями. Анализ показал, что исход зависит от параметра λ: при λ > √2/2 выигрывает Алиса, при λ < √2/2 — Базза, при λ = √2/2 — ничья.
Решение потребовало глубокого анализа оптимальных стратегий для обеих сторон. Для случая λ > √2/2 модель разработала winning strategy для Алисы, основанную на выборе достаточно большого m и игре нулями до хода 2m-1, а затем выборе значения, делающего следующий ход Баззы невозможным. Ключевым элементом было доказательство того, что максимальное значение защитной функции Баззы равно m√2, что позволило установить точное условие победы. Критический случай λ = √2/2 потребовал доказательства того, что ни один из игроков не имеет выигрышной стратегии.
Задача 6 (Комбинаторная оптимизация)
Модель сообщила только тривиальную верхнюю границу 4048 для задачи о минимальном числе плиток.
Эта задача оказалась наиболее проблематичной для модели, поскольку требовала сложной комбинаторной оптимизации размещения прямоугольных плиток на сетке 2025×2025 таким образом, чтобы в каждой строке и столбце был ровно один непокрытый квадрат. Тривиальная верхняя граница 4048 получается из подхода размещения по одной плитке в каждой строке и столбце, но оптимальное решение, вероятно, значительно меньше. Неспособность модели найти более точную оценку указывает на ограничения текущих LLM в задачах дискретной оптимизации высокой размерности.
Преодоление ограничений
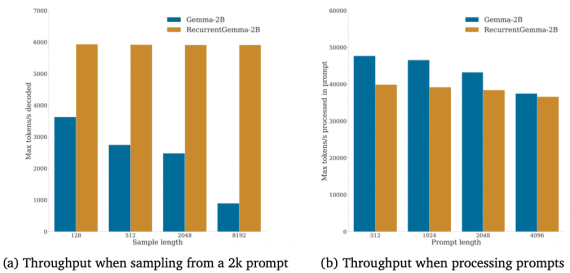
Ограничения вычислительного бюджета: максимальное количество токенов размышления Gemini 2.5 Pro составляет 32768, что недостаточно для полного решения типичной задачи IMO. Разбиение процесса на этапы позволяет эффективно использовать дополнительные бюджеты для продолжения размышления.
Избежание загрязнения данных: использование реальных задач IMO 2025 обеспечивает чистое тестирование способностей модели без утечки данных.
Значение результатов
Исследование продемонстовали, что мощные существующие модели уже способны решать сложные задачи математического рассуждения, но прямое их использование может приводить к плохим результатам. Разработанный подход показывает значительный прогресс в математическом рассуждении для LLM.
Результаты указывают на то, что при правильной методологии современные LLM могут достигать уровня, сопоставимого с медалистами математических олимпиад, открывая новые возможности для применения ИИ в математических исследованиях и образовании.