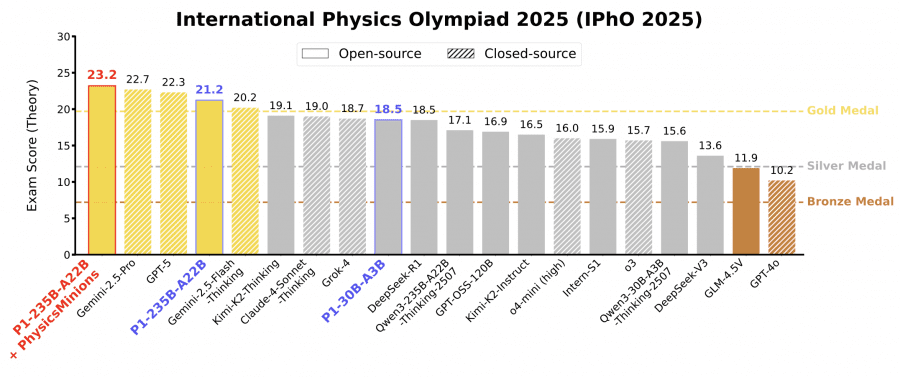
Модель P1-235B-A22B от Shanghai AI Laboratory стала первой открытой моделью, которая получила золотую медаль на последней Международной физической олимпиаде IPhO 2025, набрав 21.2 балла из 30 и заняв третье место после Gemini-2.5-Pro и GPT-5. Это довольно неожиданный результат для открытой модели. Версия P1-30B-A3B, тоже показала отличные результаты — серебряную медаль на IPhO 2025, обойдя практически все другие открытые модели. В сочетании с агентной системой PhysicsMinions модель P1-235B-A22B заняла первое место на IPhO 2025. Семейство моделей и веса P1 опубликованы в открытом доступе на Github и HuggingFace.
Что такое P1 и зачем это нужно
ИИ сделал важный шаг: от простого решения головоломок к настоящему научному мышлению. Теперь важно не просто получить ответ, который засчитают по критериям, а найти решение, которое реально работает по законам физики.
Физика — это самый строгий тест такой способности, потому что она фундаментально связывает абстрактные символы с реальностью и служит основой большинства современных технологий.
Освоение физики требует не просто запоминания фактов или применения формул — нужно концептуальное понимание, декомпозиция системы и точное многошаговое рассуждение, основанное на физических законах. Эти навыки наиболее строго проверяются на олимпиадах, таких как Международная физическая олимпиада International Physics Olympiad, IPhO, где решение каждой задачи требует и аналитической точности, и творческого подхода.
Исследователи создали P1 — семейство моделей, обученных полностью через обучение с подкреплением (RL) на базе моделей Qwen3 с режимом развернутого мышления. P1-30B-A3B обучалась на базе Qwen3-30B-A3B-Thinking-2507, а P1-235B-A22B — на базе Qwen3-235B-A22B-Thinking-2507. Модели комбинируют train-time scaling — улучшение во время обучения через RL, и test-time scaling — адаптивное развертывание через агентное управление во время инференса.
Датасет для обучения
Для обучения P1 исследователи собрали специальный датасет из 5,065 текстовых задач физического уровня олимпиад. Датасет включает 4,126 задач с физических олимпиад и 939 задач из учебников для соревнований, охватывая 5 областей физики и 25 подобластей. Вместо того чтобы гнаться за широким охватом, исследователи сосредоточились на глубине и строгости — физические олимпиады уникально сочетают абстрактное мышление с эмпирическими законами, предоставляя требовательный тренировочный датасет для улучшения и оценки способности моделей к рассуждениям в рамках физических ограничений.
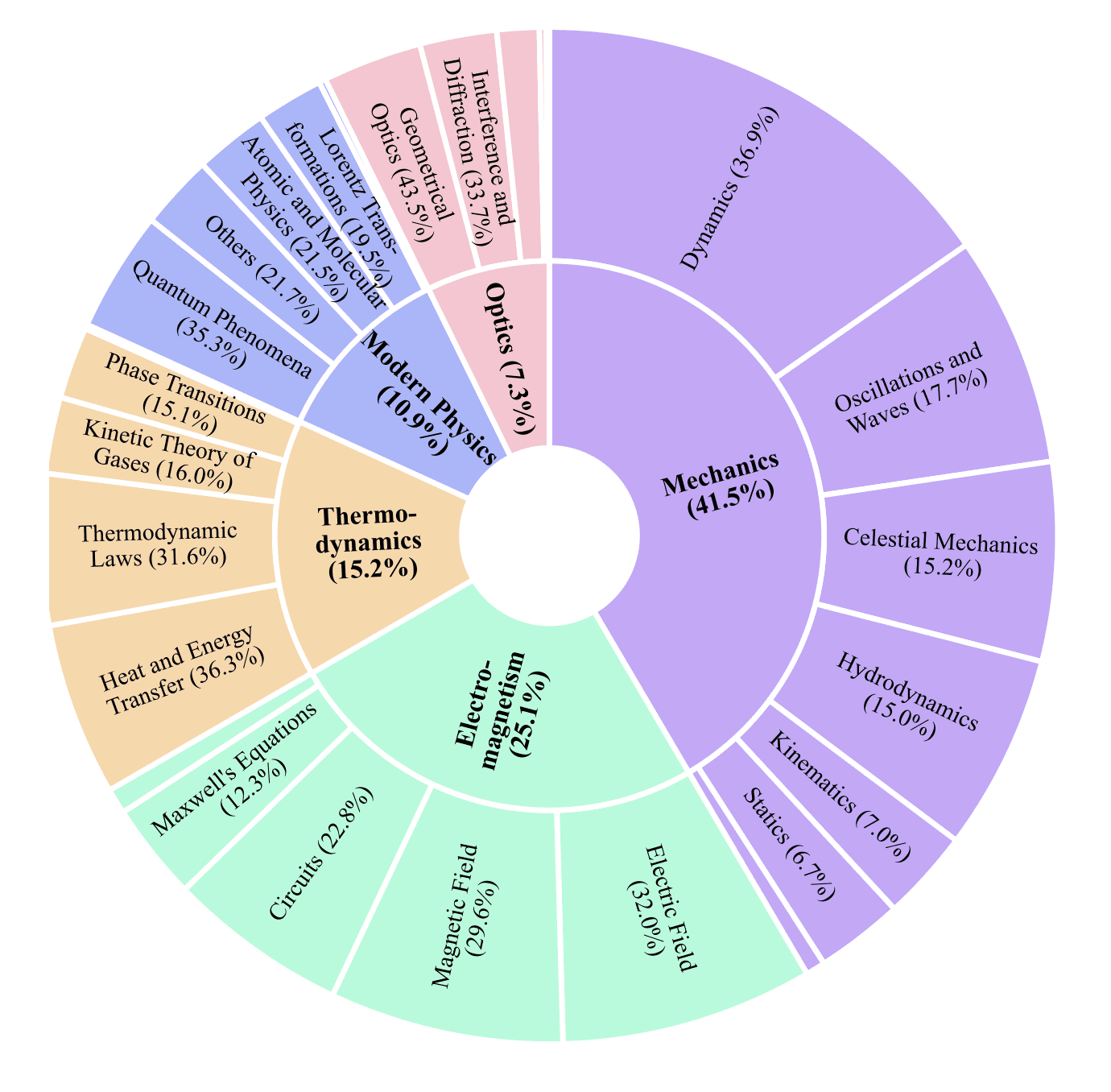
Каждый образец в датасете следует структурированной схеме Вопрос-Решение-Ответ с метаданными. Формулировки задач сохранены в оригинальном виде, когда это возможно. Решения написаны экспертами-физиками, обеспечивая аутентичные траектории рассуждений. Верифицируемые финальные ответы предоставляют однозначные критерии правильности, необходимые для обучения с подкреплением через верификацию вознаграждений (Reinforcement Learning with Verifiable Rewards, RLVR). Аннотации типа, единиц измерения и оценочных баллов поддерживают надежную валидацию и отражают взвешенные критерии человеческого оценивания. Каждый образец помечен областью физики и источником, что позволяет анализировать охват предметной области и изучать влияние происхождения данных на динамику обучения.
Подход к обучению
P1 обучается через многоэтапный фреймворк reinforcement learning (обучение с подкреплением, RL). Исследователи формулируют задачу решения физических олимпиадных задач как процесс Марковского процесса принятия решений (Markov Decision Process, MDP), где состояние — это контекст модели (включая формулировку задачи и все ранее сгенерированные шаги рассуждения), действие — это следующий токен из словаря, а функция вознаграждения оценивает правильность и качество финального решения.
Для оптимизации используется Group Sequence Policy Optimization (GSPO) — метод, который поднимает оптимизацию с уровня токенов на уровень последовательностей, используя соотношения важности правдоподобия последовательностей, нормализованные по длине. Это помогает снизить дисперсию и улучшить стабильность обучения.
Дизайн функции вознаграждения
Следуя дизайну «правильно-или-нет» в методах RLVR, исследователи используют бинарную схему вознаграждений, основанную на правильности ответа. Однако физические задачи часто включают несколько подвопросов или требуют нескольких финальных результатов. Чтобы учесть эту структуру, применяется аггрегация вознаграждений в стиле тест-кейсов, похожая на оценку программ: финальное вознаграждение R = (1/N) × Σr_i, где N — количество требуемых подответов в задаче, а r_i — индикатор правильности для i-го подответа.
Дизайн верификатора
Для обработки присущей сложности физических ответов, которые часто появляются как символьные выражения, а не одиночные числовые значения, исследователи применили гибридный фреймворк верификации, интегрирующий как rule-based (основанные на правилах), так и model-based (основанные на моделях) компоненты. Rule-based верификатор комбинирует символьные вычисления с проверками на основе правил, используя SymPy и эвристики math-verify. Model-based верификатор использует большую языковую модель Qwen3-30B-A3B-Instruct-2507 как верификатор на уровне ответов, улучшая робастность в случаях, которые сложны для чисто символьных методов.
Механизмы стабилизации обучения
Обучение через reinforcement learning часто сталкивается с проблемой: модель быстро улучшается поначалу, но потом упирается в «потолок» и перестает учиться. Это происходит из-за коллапса энтропии, разреженных вознаграждений или плохого качества данных.
Исследователи придумали два способа решить эту проблему. Первый — фильтрация датасета перед обучением. Они убирают слишком легкие задачи (которые модель решает в 70%+ случаев) и слишком сложные (которые вообще не решаются), оставляя только те, на которых модель может реально учиться. Второй способ — динамическое расширение пространства поиска по мере того, как модель становится умнее: увеличивают количество попыток на задачу и максимальную длину ответа.
Стабилизация обучения
Обнаружилась проблема с инфраструктурой. Современные RL-системы для производительности разделяют процессы: быстрые движки (vllm, SGLang) генерируют ответы модели, а тяжелые системы обучения (Megatron) обновляют веса. Но они работают с разной числовой точностью и используют разные оптимизации вычислений. В результате одна и та же операция даёт чуть-чуть разные результаты в двух системах — и это накапливается, создавая шум в градиентах. Метод Truncated Importance Sampling решает проблему, пересчитывая веса с учётом этих расхождений.
Результаты на физических олимпиадах
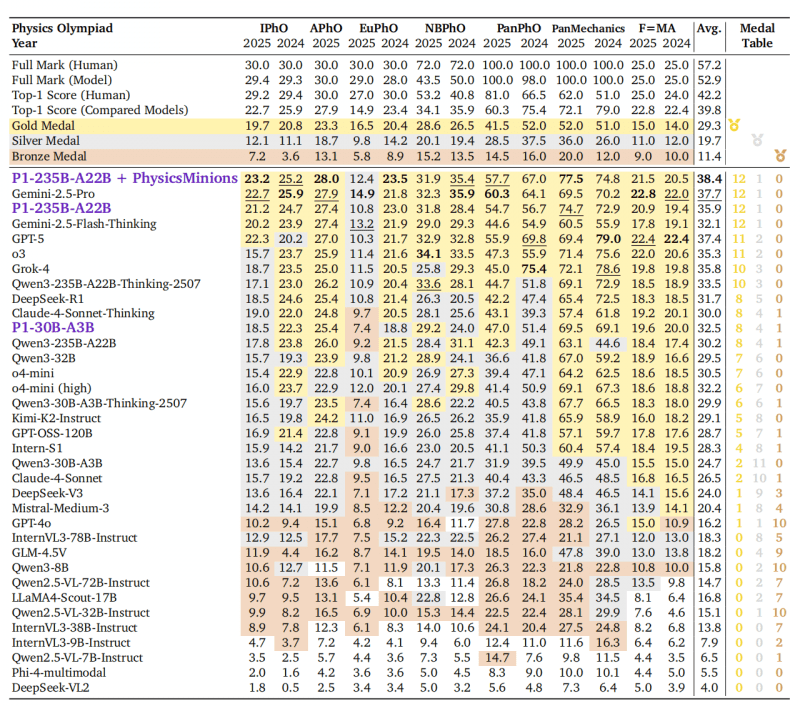
Для оценки P1 исследователи использовали бенчмарк HiPhO — набор из 13 недавних физических олимпиад 2024-2025 годов, от международных до региональных.
P1-235B-A22B показала выдающиеся результаты: набрала 21.2 из 30 баллов на Международной физической олимпиаде (IPhO 2025) и заняла 3-е место в мире — после Gemini-2.5-Pro (22.7) и GPT-5 (22.3). Это первая открытая модель, получившая золотую медаль на IPhO 2025. Всего на 13 олимпиадах модель выиграла 12 золотых и 1 серебряную медаль, обойдя проприетарные модели Grok-4 и Claude-4-Sonnet-Thinking.
P1-30B-A3B, младшая версия, заработала серебро на IPhO 2025, заняв 8-е место из 35 протестированных моделей. Она обошла почти все другие open-source модели, включая сопоставимые по размеру Qwen3-32B и Qwen3-30B-A3B-Thinking-2507, что показывает высокую эффективность обучения.
Усиление через агентов
В комбинации с агентской системой PhysicsMinions средний результат P1 улучшается с 35.9% до 38.4%, что выводит модель на первое место среди всех моделей, впереди Gemini-2.5-Pro (37.7%) и GPT-5 (37.4%).
PhysicsMinions включает три взаимодействующих компонента: Visual Studio для визуального анализа, Logic Studio для логических рассуждений и Review Studio для проверки решений. Система реализует итеративную рефлексию — P1 может рассуждать, критиковать собственные решения и улучшать их, подобно тому, как работают физики-исследователи.
Обобщаемость P1
Исследователи провели пост-тренинг на специализированном датасете для улучшения способностей решения физических задач. Помимо улучшений в конкретной предметной области, они дополнительно исследовали: сохраняет ли или даже улучшает ли модель P1 свою общую способность к рассуждениям в математике, STEM и областях программирования? Модели P1 сравнили с их соответствующими базовыми моделями на разнообразных бенчмарках: шести математических датасетах (AIME24, AIME25, HMMT, IMO-AnswerBench, AMOBench, BeyondAIME), двух STEM-ориентированных оценках (GPQA, HLE), одном бенчмарке программирования (LiveCodeBench) и задаче общего рассуждения (LiveBench).
Примечательно, что модели P1 последовательно демонстрируют преимущества над своими базовыми аналогами: P1-30B-A3B превосходит Qwen3-30B-A3B-Thinking-2507 по всем метрикам, в то время как P1-235B-A22B достигает лучшей производительности по сравнению с Qwen3-235B-A22B-Thinking-2507 в части категорий. Этот паттерн подчеркивает, что модели P1 не только поддерживают, но и улучшают общие способности к рассуждениям за пределами целевой области — даже на более сложных математических бенчмарках (например, IMO-AnswerBench, AMOBench), которые тестируют продвинутые навыки решения задач.
Эти результаты предполагают, что сфокусированный на предметной области пост-тренинг может индуцировать переносимые улучшения в общем рассуждении. Исследователи выдвигают гипотезу о двух способствующих факторах. Во-первых, процесс оптимизации уточняет траектории рассуждений способом, который выходит за границы предметных областей, позволяя стратегиям, полезным для математики, STEM и задач программирования, появляться. Во-вторых, тренировочный датасет, хотя и специализированный, разделяет структурные сходства с другими областями — такие как строгая символьная манипуляция, многошаговая логическая дедукция и абстрактное моделирование задач — которые лежат в основе общего рассуждения.
Важный урок про верификаторы
Из-за сложности реализации всеобъемлющего и полностью правильного механизма верификации, основанного исключительно на правилах, исследователи разработали гибридный верификатор, интегрирующий рассуждения как на основе правил, так и на основе моделей для достижения более широкого охвата. Однако они обнаружили, что применение model-based верификатора непосредственно в процессе пост-тренинга может быть рискованным.
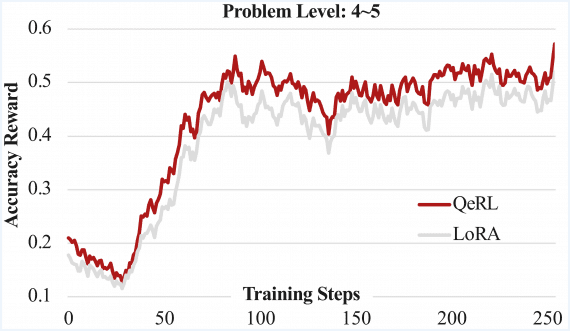
При сравнении динамики тренировки с model-based верификатором и без него наблюдается, что вариант, использующий model-based верификатор, демонстрирует взрывной рост длины ответа, но его производительность на валидации ухудшается по сравнению с настройкой, использующей только rule-based верификатор.
Исследователи приписывают этот феномен двум основным причинам:
- Model-based верификатор восприимчив к взлому со стороны модели политики. Поскольку сам верификатор является языковой моделью, он может развить непреднамеренные смещения, предпочитая нетипичные паттерны ответов, такие как чрезмерно многословные или стилистически своеобразные ответы, которые могут быть использованы policy model для получения искусственно высоких вознаграждений.
- Негативное влияние false positive срабатываний, то есть неправильного вознаграждения неправильных ответов, существенно более вредно, чем false negatives, то есть пропуска некоторых правильных ответов.
Это можно понять в терминах verification precision (точности верификации) и verification recall (полноты верификации). Rule-based верификатор обычно предлагает высокую точность, но ограниченную полноту, в то время как model-based верификатор увеличивает полноту за счет точности. Во время обучения с подкреплением этот дисбаланс может легко дестабилизировать оптимизацию: несколько высоковознаграждаемых false positives могут доминировать в сигнале обучения, направляя политику к вырожденным паттернам решений.
Выводы
P1 представляет собой значительный шаг к LLM, которые могут участвовать в настоящем научном мышлении и в конечном итоге внести вклад во фронтир физических исследований. Успех P1 в освоении физики олимпиадного уровня представляет ключевую веху: если модели могут строго решать хорошо определенные задачи, основанные на естественных законах, они в конечном итоге могут внести вклад в исследование неизведанных научных границ.
Команда выпустила две версии моделей P1 и оценила их на HiPhO — новом бенчмарке, агрегирующем последние 13 олимпиадных экзаменов с 2024-2025 годов. Флагманская модель P1-235B-A22B достигает milestone (важной вехи) для open-source сообщества — становясь первой открытой моделью, достигшей Gold-medal performance на IPhO 2025, зарабатывая 12 золотых и 1 серебряную на полном наборе HiPhO. Облегченный вариант P1-30B-A3B достигает Silver-medal performance на IPhO 2025, превосходя практически все предыдущие open baselines. В сочетании с агентной системой PhysicsMinions P1 достигает общего места No.1 как на IPhO 2025, так и на лидербордах HiPhO.
Помимо физики, модели P1 демонстрируют замечательную обобщаемость. 30B вариант значительно превосходит свою базовую модель (Qwen3-30B-A3B-Thinking-2507) на семи бенчмарках математики, программирования и общего рассуждения, предполагая, что пост-тренинг по физике культивирует переносимые навыки рассуждения, а не переобучение на предметной области.