В предыдущем вводном туториале по нейронным сетям была создана трехслойная архитектура для классификации рукописных символов датасета MNIST. В конце туториала была показана точность приблизительно 86%. Для простого датасета, как MNIST, это плохое качество. Дальнейшая оптимизация смогла улучшить результат плотно соединенной сети до 97-98% точности. Это уже намного лучше, но всё еще не достаточно для MNIST. Требуется более современный метод, который может действительно называться глубоким обучением. В данном туториале представлен такой метод — сверточная нейронная сеть (Convolutional Neural Network, CNN), который достигает высоких результатов в задачах классификации картинок. В частности, будет рассмотрена и теория, и практика реализации CNN при помощи PyTorch.
PyTorch — набирающий популярность мощный фреймворк глубокого машинного обучения. Его особенность — он чувствует себя как дома в Python, а прототипирование осуществляется очень быстро. Туториал не предполагает больших знаний PyTorch. Весь код для сверточной нейронной сети, рассмотренной здесь, находится в этом репозитории. Давайте приступим.
Особенности CNN
Полностью соединенная нейросеть с несколькими слоями может много, но чтобы показать действительно выдающиеся результаты в задачах классификации, необходимо идти глубже. Другими словами, требуется использовать намного больше слоев в сети. Однако, добавление многих новых слоев влечет проблемы. Во-первых, сталкиваемся с проблемой забывания градиента, хотя это и можно решить при помощи чувствительной функции активации — семейства ReLU функций. Другая проблема с глубокими полностью соединенными сетями — количество весов для тренировки быстро растет. Это означает, что процесс тренировки замедляется или становится практически невыполнимым, а модель может переобучаться. Тем не менее, решение есть.
Сверточные нейронные сети пытаются решить вторую проблему, используя корреляции между смежными входами в картинках или временных рядах. Например, на картинке с котиком и собачкой пиксели, близкие к глазам котика, более вероятно будут коррелировать с расположенными рядом пикселями на его носу, чем с пикселями носа собаки на другой стороне картинки. Это означает, что нет необходимости соединять каждый узел с каждым в следующем слое. Такой прием уменьшает количество весовых параметров для тренировки модели. CNN также имеют и другие особенности, улучшающие процесс тренировки, которые будут рассмотрены в других главах.
Принцип работы CNN
Свертка — фактически главное, что необходимо понять о сверточных нейронных сетях. Этот замысловатый математический термин нужен для движущегося окна или фильтра по исследуемому изображению. Перемещающееся окно применяется к определенному участку узлов, как показано ниже. Где примененный фильтр — ( 0.5 * значение в узле):
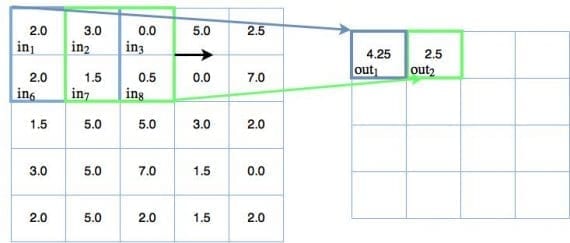
На диаграмме показаны только два выходных значения, каждое из которых отображает входной квадрат размера 2×2. Вес отображения для каждого входного квадрата, как ранее упоминалось, равен 0.5 для всех четырех входов (inputs). Поэтому выход может быть посчитан так:
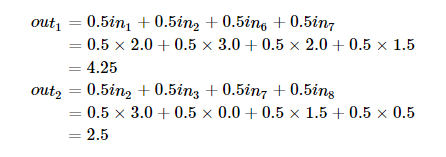
В сверточной части нейронной сети можно представить, что такой движущийся 2 х 2 фильтр скользит по всем доступным узлам или пикселям входного изображения. Такая операция может быть проиллюстрирована с использованием стандартных диаграмм узлов нейронных сетей:
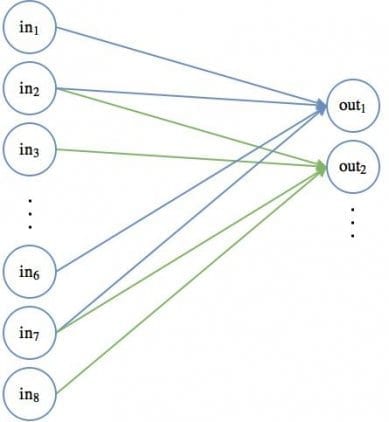
Первое положение связей движущегося фильтра показано синей линией, второе — зеленой. Веса для каждых таких соединений равны 0.5.
Вот несколько вещей в сверточном шаге, которые ускоряют процесс тренировки, сокращая количество параметров, весов:
- Редкие связи — не каждый узел в первом (входном) слое соединен с каждым узлом во втором слое. Этим отличается архитектура CNN от полностью связанной нейронной сети, где каждый узел соединен со всем другими в следующем слое.
- Постоянные параметры фильтра. Другими словами, при движении фильтра по изображению одинаковые веса применяются для каждого 2 х 2 набора узлов. Каждый фильтр может быть обучен для выполнения специфичных трансформаций входного пространства. Следовательно, каждый фильтр имеет определенный набор весов, которые применяются для каждой операции свертки. Этот процесс уменьшает количество параметров. Нельзя говорить, что любой вес постоянен внутри отдельного фильтра. В примере выше веса были [0.5, 0.5, 0.5, 0.5], но ничего не мешало им быть и [0.25, 0.1, 0.8, 0.001]. Выбор конкретных значений зависит от обучения каждого фильтра.
Эти два свойства сверточных нейронный сетей существено уменьшают количество параметров для тренировки, по сравнению с полносвязными сетями.
Следующий шаг в структуре CNN — прохождение выхода операции свертки через нелинейную активационную функцию. Речь идет о некотором подвиде ReLU, который обеспечивает известное нелинейное поведение этой нейронной сети.
Процесс, использующийся в сверточном блоке, называется признаковым отображением (feature mapping). Название основано на идее, что каждый сверточный фильтр может быть обучен для поиска различных признаков в изображении, которые затем могут быть использованы в классификации. Перед разговором о следующем свойстве CNN, называемом объединением (pooling), рассмотрим идею признакового отображения и каналов.
Отображение признаков и мультиканальность
Поскольку веса отдельных фильтров остаются постоянными, будучи примененными на входных узлах, они могут обучаться выбирать определенные признаки из входных данных. В случае изображений, архитектура способна учиться различать общие геометрические объекты — линии, грани и другие формы исследуемого объекта. Вот откуда взялось определение признакового отображения. Из-за этого любой сверточный слой нуждается в множестве фильтров, которые тренируются детектировать различные признаки. Следовательно, необходимо дополнить предыдущую диаграмму движущегося фильтра следующим образом:
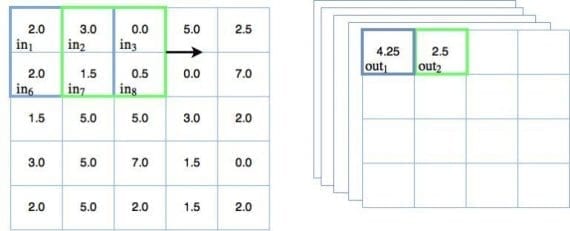
Теперь в правой части рисунка можно видеть несколько сложенных (stacked) выходов операции свертки. Их несколько, потому что существует несколько обучаемых фильтров, каждый из которых производит собственный 2D выход (в случае 2D изображения). Такое множество фильтров часто в глубоком обучении часто называют каналами. Каждый канал должен обучаться для выделения на изображении определенного ключевого признака. Выход сверточного слоя для черно-белого изображения, как в датасете MNIST, имеет 3 измерения — 2D для каждого из каналов и еще одно для их числа.
Если входной объект мультиканальный, то в случае цветного RGB изображения (один канал для каждого цвета) выход будет четырехмерным. К счастью, любая библиотека глубокого обучения, включая PyTorch, легко справляется с отображением. Наконец, не стоит забывать, что операция свертки проходит через активационную функцию в каждом узле.
Следующая важная часть сверточных нейронных сетей — концепция, называемая пулингом.
Объединение (Pooling)
Основными преимуществами для пулинга в сверточной нейронной сети являются:
- Уменьшение количества параметров в вашей модели благодаря процессу даунсемплинга (down-sampling).
- Детектирование признаков становится более правильным при изменении ориентации или размера объекта.
Пулинг — другой тип техники скользящего окна, где вместо применения обучаемых весов используется статистическая функция некоторого типа по содержимому этого окна. Наиболее частый тип пулинга — max pooling, который применяет функцию max(). Есть и другие варианты — mean pooling (который применяет функцию усреднения по содержимому окна), которые применяются в особых случаях. В этом туториале мы будем концентрироваться на max pooling. На рисунке ниже показано, как работает операция max pooling:
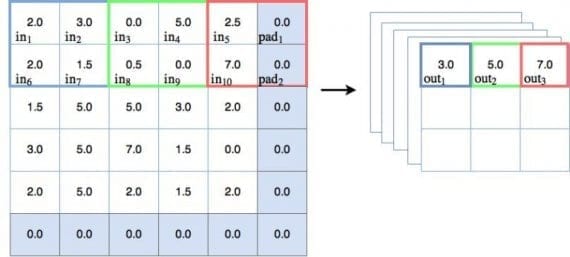
Давайте пройдемся по некоторым пунктам, связанным с диаграммой:
Основы
На диаграмме можно наблюдать действие max pooling. Для первого окна голубого цвета max pooling выдает значение 3.0, которое является максимальным значением узла в 2х2 окне. Таким же образом зеленое окно выводит максимальное значение, равно 5.0, а для красного окна максимальное значение — 7.0. Здесь всё просто и понятно.
Шаги и даунсемплинг
На диаграмме сверху можно заметить, что пулинговое окно каждый раз перемещается на 2 места. Можем говорить, что шаг равен 2. На диаграмме показаны шаги только вдоль оси x, но для задачи предотвращения перекрытия окна, шаг должен быть также равен 2 и в направлении y. Другими словами, шаг обозначается как [2,2]. Следует упомянуть, если во время пулинга шаг больше 1, тогда размер выхода будет уменьшен. Как можно видеть на диаграмме, входной объект размера 5×5 уменьшается до 3х3 на выходе. И это хорошо — такое явление называется даунсемплингом и уменьшает количество обучаемых параметров в модели.
Padding
Важно отметить также, что в пулинговой диаграмме есть дополнительный столбец и строка, добавленные к входу размера 5х5, делающие эффективный размер пулингового пространства равным 6х6. Это делается для того, чтобы пулинговое окно размером 2х2 корректно работало с шагом [2,2]. Такой прием называется padding. Padding-узлы зачастую фиктивные, так как значения на них равны 0, и операция max pooling их не видит. Этот факт нужно будет учитывать при создании нашей сверточной сети на PyTorch.
Теперь мы разобрались в механизме работы пулинга в CNN, выяснили его полезность в осуществлении даунсемплинга. Рассмотрим еще его некоторые функции и ответим на вопрос, почему max pooling используется так часто.
Использование пулинга в сверточных нейронных сетях
В дополнении к функции даунсемплинга пулинг используется в CNN, чтобы детектировать определенные признаки, инвариантные к изменениям размера или ориентации. Другой способ представить действие пулинга — он обобщает низкоуровневую, сложно структурированную информацию. Представим случай, когда у нас есть сверточный фильтр, который во время тренировки обучается распознавать знак «9» в различных положениях на входном изображении. Чтобы сверточная сеть научилась корректно классифицировать появление «9» на картинке, требуется каким-то образом активировать сеть каждый раз, когда эта цифра появляется на изображении независимо от размера и ориентации (кроме случая, когда «9» напоминает «9»). Пулинг может помочь в такой задаче выбора высокоуровневых, обобщенных признаков. Этот процесс иллюстрирован ниже:
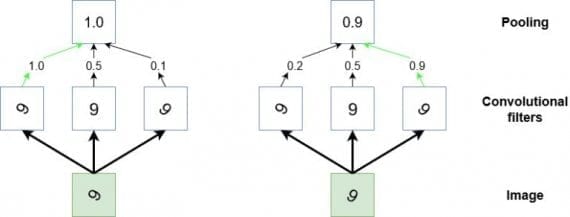
Диаграмма — стилизованное представление операции пулинга. Если мы считаем, что маленький участок входного изображения содержит цифру 9 (зеленый квадрат), и предполагаем, что пытаемся детектировать эту цифру на изображении. В таком случае несколько сверточных фильтров обучаются активироваться с помощью ReLU функции каждый раз, когда они видят «9» на картинке. Однако, они будут активироваться более или менее сильно в зависимости от того, как она расположена. Мы хотим научить сеть обнаруживать цифру на изображении независимо от ее ориентации. Здесь наступает черед пулинга. Он«смотрит» на выходы трех фильтров и берет настолько высокое значение, насколько высокий порог функций активации этих фильтров.
Следовательно, пулинг выступает в качестве механизма обобщения низкоуровневых данных и позволяет нейросети переходить от данных с высоким разрешением до информации с более низким разрешением. Другими словами, пулинг в паре со сверточными фильтрами делают возможным детектирование объекта на изображении.
Общий взгляд
Ниже представлено изображение из Википедии, которое показывает структуру полностью разработанной сверточной нейронной сети:
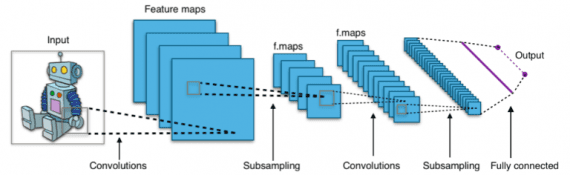
Если смотреть на рисунок сверху слева направо, сначала мы видим изображение робота. Далее серия сверточных фильтров сканирует входное изображение для отображения признаков. Из выходов этих фильтров операции пулинга выбирают подвыборку. После этого идет следующий набор сверток и пулинга на выходе из первого набора операций пулинга и свертки. Наконец, на выходе нейросети находится прикрепленный полносвязный слой, смысл которого нуждается в объяснении.
Полносвязный слой
Ранее обсуждалось, сверточная нейронная сеть берет данные высокого разрешения и эффективно трансформирует их в представления объектов. Полносвязный слой может рассматриваться как стандартный классификатор над богатым информацией выходом нейросети для интерпретации и финального предсказания результата классификации. Для прикрепления полносвязного слоя к сети измерения выхода CNN необходимо «расплющить».
Рассматривая предыдущую диаграмму, на выходе имеем несколько каналов x x y тензоров/матриц. Эти каналы необходимо привести к одному (N x 1) тензору. Возьмем пример: имеем 100 каналов с 2х2 матрицами, отображающими выход последней пулинг операции в сети. В PyTorch можно легко осуществить преобразование в 2х2х100 = 400 строк, как будет показано ниже.
Теперь, когда основы сверточных нейронных сетей заложены, настало время реализовать CNN с помощью PyTorch.
Реализация CNN на PyTorch
Любой достойный фреймворк глубокого обучения может с легкостью справиться с операциями сверточной нейросети. PyTorch является таким фреймворком. В данном разделе будет показано, как создавать CNN с помощью PyTorch шаг за шагом. В идеале вы должны обладать некоторым представлением о PyTorch, но это не обязательно. Мы хотим разработать нейронную сеть для классификации символов в датасете MNIST. Полный код к этому туториалу находится в этом репозитории на GitHub.
Мы собираемся реализовать следующую архитектуру сверточной сети:
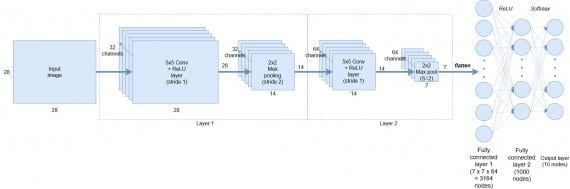
В самом начале на вход подаются черно-белые представления символов размером 28х28 пикселей каждое. Первый слой состоит из 32 каналов сверточных фильтров размера 5х5 + активационная функция ReLU, затем идет 2х2 max pooling с даунсемплингом с шагом 2 (этот слой выводит данные размером 14х14). На следующий слой подается выход с первого слоя размера 14х14, который сканируется снова 5х5 сверточными фильтрами с 64 каналов, затем следует 2х2 max pooling с даунсемплингом для генерирования выхода размером 7х7.
После сверточной части сети следует:
- операция выравнивания, которая создает 7х7х64=3164 узлов
- средний слой из 1000 полносвязных улов
- операция softmax над крайними 10 узлами для генерирования вероятностей классов.
Эти слои представлены в выходном классификаторе.
Загрузка датасета
В PyTorch уже интегрирован датасет MNIST, который мы можем использовать при помощи функции DataLoader. В этом подразделе выясним, как установить загрузчик данных для датасета MNIST. Но для начала нужно определить предварительные переменные:
num_epochs = 5 num_classes = 10 batch_size = 100 learning_rate = 0.001 DATA_PATH = 'C:UsersAndyPycharmProjectsMNISTData' MODEL_STORE_PATH = 'C:UsersAndyPycharmProjectspytorch_models'
Прежде всего, устанавливаем тренировочные гиперпараметры. Далее идет спецификация пути папки для хранения датасета MNIST (PyTorch автоматически загрузит датасет в эту папку) и локации для тренировочных параметров модели после того, как обучение будет завершено.
Далее задаем преобразование для применения к MNIST и переменные для данных:
trans = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) train_dataset = torchvision.datasets.MNIST(root=DATA_PATH, train=True, transform=trans, download=True) test_dataset = torchvision.datasets.MNIST(root=DATA_PATH, train=False, transform=trans)
Первое, на что необходимо обратить внимание в коде сверху, это функция transform.Compose(). Функция находится в пакете torchvision. Она позволяет разработчику делать различные манипуляции с указанным датасетом. Численные трансформации могут быть соединены вместе в список при использовании функции Compose(). В этом случае сначала устанавливается преобразование, которое конвертирует входной датасет в PyTorch тензор. PyTorch тензор — особый тип данных, используемый в библиотеке для всех различных операций с данными и весами внутри нейросети. По сути, такой тензор — простая многомерная матрица. Но в любом случае, PyTorch требует преобразования датасета в тензор таким образом, что его можно использовать для тренировки и тестирования сети.
Следующий аргумент в списке Compose() — нормализация. Нейронная сеть обучается лучше, когда входные данные нормализованы так, что их значения находятся в диапазоне от -1 до 1 или от 0 до 1. Чтобы это сделать с помощью нормализации PyTorch, необходимо указать среднее и стандартное отклонение MNIST датасета, которые в этом случае равны 0.1307 и 0.3081 соответственно. Отметим, среднее значение и стандартное отклонение должны быть установлены для каждого входного канала. У MNIST есть только один канал, но уже для датасета CIFAR c 3 каналами (по одному на каждый цвет из RGB спектра) надо указывать среднее и стандартное отклонение для каждого.
Далее необходимо создать объекты train_dataset и test_dataset, которые будут последовательно проходить через загрузчик данных. Чтобы создать такие датасеты из данных MNIST, требуется задать несколько аргументов. Первый — путь до папки, где хранится файл с данными для тренировки и тестирования. Логический аргумент train показывает, какой файл из train.pt или test.pt стоит брать в качестве тренировочного сета. Следующий аргумент — transform, в котором мы указываем ранее созданный объект trans, который осуществляет преобразования. Наконец, аргумент загрузки просит функцию датасета MNIST загрузить при необходимости данные из онлайн источника.
Теперь когда тренировочный и тестовый датасеты созданы, настало время загрузить их в загрузчик данных:
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size,shuffle=True) test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)
Объект загрузчик данных в PyTorch обеспечивает несколько полезных функций при использовании тренировочных данных:
- Возможность легко перемешивать данные.
- Возможность группировать данные в партии.
- Более эффективное использование данных с помощью параллельной загрузки, используя многопроцессорную обработку.
Как можно видеть, требуется задать три простых аргумента. Первый — данные, которые вы хотите загрузить; второй — желаемый размер партии; третий — перемешивать ли случайным образом датасет. Загрузчик может использоваться в качестве итератора. Поэтому для извлечения данных мы можем просто воспользоваться стандартным итератором Python, например, перечислением. Такая возможность будет позже продемонстрирована на практике в туториале.
Создание модели
На этом шаге необходимо задать класс nn.Module, определяющий сверточную нейронную сеть, которую мы хотим обучить:
class ConvNet(nn.Module): def __init__(self): super(ConvNet, self).__init__() self.layer1 = nn.Sequential( nn.Conv2d(1, 32, kernel_size=5, stride=1, padding=2), nn.ReLU(), nn.MaxPool2d(kernel_size=2, stride=2)) self.layer2 = nn.Sequential( nn.Conv2d(32, 64, kernel_size=5, stride=1, padding=2), nn.ReLU(), nn.MaxPool2d(kernel_size=2, stride=2)) self.drop_out = nn.Dropout() self.fc1 = nn.Linear(7 * 7 * 64, 1000) self.fc2 = nn.Linear(1000, 10)
Это то место, где определяется модель. Наиболее простой способ создания структуры нейронной сети в PyTorch — создание наследственного класса от материнского nn.Module. Класс nn.Module очень полезен в PyTorch, он содержит всё необходимое для конструирования типичной глубокой нейронной сети. Кроме этого, класс имеет удобные функции: способы перемещения переменных и операций на GPU или обратно на CPU, применение рекурсивных функций через все свойства в классе (например, перенастройка всех весовых переменных), создание оптимизированных интерфейсов для тренировки и тому подобное. Все доступные методы можно посмотреть здесь.
Первый шаг — создание нескольких объектов последовательного слоя с помощью функции class _init_. Сначала создаем слой 1 (self.layer1) через создание объекта nn.Sequential. Этот метод позволяет создавать упорядоченные слои в сети и является удобным способом создания последовательности свертка + ReLu + пулинг. Как можно видеть, первый элемент в определении этой последовательности — метод Conv2d, который создает набор сверточных фильтров. В этом методе первый аргумент — количество входных каналов; в нашем случае изображения MNIST черно-белые и количество каналов равно 1. Второй аргумент в Conv2d — количество выходных каналов; как показано на диаграмме архитектуры модели, первый слой сверточных фильтров состоит из 32 каналов, поэтому значение второго аргумента равно 32.
Аргумент kernel_size отвечает за размер сверточного фильтра, в нашем случае мы хотим фильтр размеров 5х5, поэтому аргумент равен 5. Если бы мы хотели фильтры с разными размерными формами по оси х и y, необходимо было указать параметры в виде python tuple (размер по х, размер по y). Наконец, мы хотим установить padding, что делается несколько сложнее. Размер измерения на выходе от операции сверточной фильтрации или пулинга может быть посчитан с помощью уравнения:
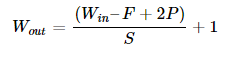
Где W(in) — ширина выхода, F — размер фильтра, P — паддинг, S — шаг. Такая же формула применима для расчета высоты. В нашем случае изображение и фильтрация симметричны, поэтому формула применима и к ширине и к высоте. Если хотим оставить входные и выходные измерения без изменений с размером фильтра 5 и шагом 1, то исходя из верхней формулы паддинг нужно задать равным 2. Таким образом, аргумент для паддинга в Conv2d равен 2.
Следующий аргумент в последовательности — простая ReLU функция активации. Последний элемент в последовательном определении для self.layer1 — операция max pooling. Первый аргумент — размер объединения, который равен 2х2; следовательно, аргумент равен 2. Во втором аргументе мы хотим взять подвыборку из данных через уменьшение эффективного размера изображения с факторов 2. Чтобы это сделать используя формулу выше, устанавливаем шаг равным 2 и паддинг равным 0. Следовательно, шаговый аргумент равен 2. Паддинг аргумент по умолчанию равен 0, если не указано другое значение, что сделано в коде сверху. Из этих вычислений теперь понятно, что выход слоя self.layer1 имеет 32 канала и “изображения” размером 14х14.
Второй слой, self.layer2, определяется таким же образом, как и первый. Единственное отличие здесь — вход в функцию Conv2d теперь 32 канальный, а выход — 64 канальный. Следуя такой же логике и учитывая пулинг и даунсемплинг, выход из self.layer2 представляет из себя 64 канала изображения размера 7х7.
Далее определяем отсеивающий слой для предотвращения переобучения модели. В конце создаем два полносвязных слоя. Первый слой имеет размер 7х7х64 узла и соединяется со вторым слоем с 1000 узлами. Чтобы создать полносвязный слой в PyTorch, используем метод nn.Linear. Первый аргумент метода — число узлов в данном слое, второй аргумент — число узлов в следующем слое.
Определение слоев создано при помощи _init_. Следующий шаг — определить потоки данных через слои при прямом прохождении через сеть:
def forward(self, x): out = self.layer1(x) out = self.layer2(out) out = out.reshape(out.size(0), -1) out = self.drop_out(out) out = self.fc1(out) out = self.fc2(out) return out
Здесь важно назвать функцию “forward”, так как она будет использовать базовую функцию прямого распространения в nn.Module и позволит всему функционалу nn.Module работать корректно. Как можно видеть, функция принимает на вход аргумент х, представляющий собой данные, которые должны проходить через модель (например, партия данных). Направляем эти данные в первый слой (self.layer1) и возвращаем выходные данные как out. Эти выходные данные поступают на следующий слой и так далее. Отметим, после self.layer2 применяем функцию преобразования формы к out, которая разглаживает размеры данных с 7х7х64 до 3164х1. После двух полносвязных слоев применяется dropout-слой и из функции возвращается финальное предсказание.
Мы определили, что такое сверточная нейронная сеть, и как она работает. Настало время обучить нашу модель.
Обучение модели
Перед тренировкой модели мы должны сначала создать экземпляр (instance) нашего класса ConvNet(), определить функцию потерь и оптимизатор:
model = ConvNet() criterion = nn.CrossEntropyLoss() optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
Экземпляр класса ConvNet() создается под названием model. Далее определяем операцию над потерями, которая будет использоваться для подсчета потерь. В нашем случае используем доступную в PyTorch функцию CrossEntropyLoss(). Вы уже могли заметить, что мы еще не задали активационную функцию SoftMax для последнего слоя, выполняющего классификацию. Это сделано потому, что функция CrossEntropyLoss() объединяет и SoftMax и кросс-энтропийную функцию потерь в единую функцию. Далее определяем оптимизатор Adam. Первым аргументом функции являются параметры, которые мы хотим обучить оптимизатором. Это легко сделать с помощью класса nn.Module, из которого вы получается ConvNet. Всё что нужно сделать — снабдить функцию аргументом model.parameters() и PyTorch будет отслеживать все параметры нашей модели, которые необходимо обучить. Последним определяется скорость обучения.
Тренировочный цикл выглядит следующим образом:
total_step = len(train_loader) loss_list = [] acc_list = [] for epoch in range(num_epochs): for i, (images, labels) in enumerate(train_loader): # Прямой запуск outputs = model(images) loss = criterion(outputs, labels) loss_list.append(loss.item()) # Обратное распространение и оптимизатор optimizer.zero_grad() loss.backward() optimizer.step() # Отслеживание точности total = labels.size(0) _, predicted = torch.max(outputs.data, 1) correct = (predicted == labels).sum().item() acc_list.append(correct / total) if (i + 1) % 100 == 0: print('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}, Accuracy: {:.2f}%' .format(epoch + 1, num_epochs, i + 1, total_step, loss.item(), (correct / total) * 100))
Самыми важными частями для начала являются два цикла. Первый цикл проходит по количеству эпох, в нём итерации проходят по train_loader используя перечисление. Во внутреннем цикле сначала считаются выходы прямого прохождения изображений (которые представляют собой партии нормализованных MNIST изображений из train_loader). Отметим, нам не требуется вызывать model.forward(images), так как nn.Module знает, что нужно вызывать forward при выполнении model(images).
Следующий шаг — отправление выходов модели и настоящих меток в функцию CrossEntropyLoss, определенную как criterion. Потери добавляются в список, который будет использован позже для отслеживания прогресса обучения. Затем — выполнение обратного распространения ошибки и оптимизированного шага тренировки. Сначала градиенты должны быть обнулены, что легко делается вызовом zero_grad() на оптимизаторе. Далее вызываем функцию .backward() на переменной loss для выполнения обратного распространения. Теперь, когда градиенты посчитаны при обратном распространении, просто вызываем optimizer.step() для выполнения шага обучения оптимизатора Adam. PyTorch делает процесс обучения модели очень легким и интуитивным.
Следующий набор строк отвечает за отслеживание точности на тренировочном сете. Предсказания модели могут быть определены с помощью функции torch.max(), которая возвращает индекс максимального значения в тензоре. Первый аргумент этой функции — тензор, который мы хотим исследовать; второй — ось, по которой определяется максимум. Выходящий из модели тензор должен иметь размер (batch_size,10). Чтобы определить предсказание модели, необходимо для каждого примера в партии найти максимальные значения из 10 выходных узлов. Каждый из этих узлов будет соответствовать одному рукописному символу (например, выход 2 равен символу «2» и так далее). Выходной узел с наибольшим значением и будет предсказанием модели. Следовательно, надо задать второй аргумент в функции torch.max() равным 1, что указывает функции максимума проверить ось выходного узла (axis = 0 соответствует размерности batch_size).
На этом шаге возвращается список целочисленных предсказаний модели, а следующая строка сравнивает эти предсказания с настоящими метками (predicted == labels) и суммирует правильные предсказания. Отметим, что на этом шаге выход функции sum() всё еще тензор, поэтому для оценки его значений требуется вызвать .item(). Делим количество правильных предсказаний на размер партии batch_size (эквивалентно labels.size(0)) для подсчета точности. Наконец, во время тренировки после каждых 100 итераций внутреннего цикла выводим прогресс.
Результаты тренировки будут выглядеть следующим образом:
Epoch [1/6], Step [100/600], Loss: 0.2183, Accuracy: 95.00%
Epoch [1/6], Step [200/600], Loss: 0.1637, Accuracy: 95.00%
Epoch [1/6], Step [300/600], Loss: 0.0848, Accuracy: 98.00%
Epoch [1/6], Step [400/600], Loss: 0.1241, Accuracy: 97.00%
Epoch [1/6], Step [500/600], Loss: 0.2433, Accuracy: 95.00%
Epoch [1/6], Step [600/600], Loss: 0.0473, Accuracy: 98.00%
Epoch [2/6], Step [100/600], Loss: 0.1195, Accuracy: 97.00%
Теперь напишем код для определения точности на тестовом наборе.
Тестирование
Для тестирования модели используем следующий код:
model.eval() with torch.no_grad(): correct = 0 total = 0 for images, labels in test_loader: outputs = model(images) _, predicted = torch.max(outputs.data, 1) total += labels.size(0) correct += (predicted == labels).sum().item() print('Test Accuracy of the model on the 10000 test images: {} %'.format((correct / total) * 100)) # Сохраняем модель и строим график torch.save(model.state_dict(), MODEL_STORE_PATH + 'conv_net_model.ckpt')
В первой строке устанавливаем режим оценки используя model.eval(). Это удобная функция запрещает любые исключения или слои нормализации партии в модели, которые будут мешать объективной оценке. Конструкция torch.no_grad() выключает функцию автоградиента в модели, так как она не нужна при тестировании/оценке модели и замедляет вычисления. Остальная часть кода совпадает с вычислением точности во время тренировки, за исключением того, что в этом случае итерации проходят по test_loader.
Наконец, результат выводится в консоль, а модель сохраняется при помощи функции torch.save().
В последней части кода в этом репозитории на GitHub дополнительно построен график отслеживания точности и потерь, используя библиотеку для рисования Bokeh. Финальный результат выглядит так:
Точность на тестовой выборке на 10000 картинках составляет 99.03%
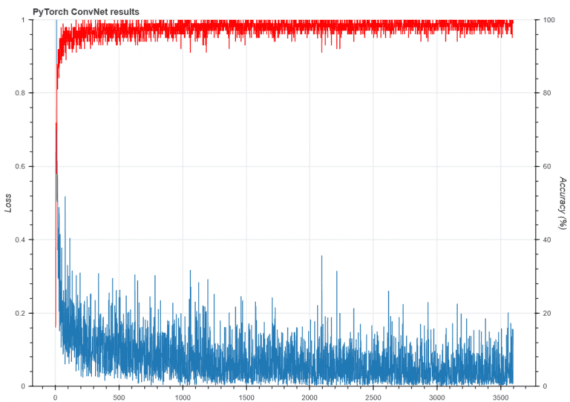
Можно видеть, сеть достаточно быстро достигает высокого уровня точности на тренировочном сете. На тестовом наборе после 6 эпох модель показывает точность 99%, что очень хорошо. Этот результат определенно лучше точности базовой полносвязной нейронной сети.
Как итог: в туториале были показаны все преимущества и структура сверточной нейронной сети, механизм её работы. Вы также научились реализовывать CNN в библиотеке глубокого обучения PyTorch, которая имеет большое будущее.
Интересные статьи: