
Если вы уже пробовали создавать собственные глубокие нейронные сети с помощью TensorFlow и Keras, то, вероятно, знакомы с чувством разочарования при отлаживании этих библиотек. Хотя они имеют API на Python, всё еще трудно выяснить, что именно пошло не так при ошибке. Они также плохо работают вместе с библиотеками numpy, scipy, scikit-learn, Cython и другими. Библиотека глубокого обучения PyTorch имеет заявленное преимущество — хорошо работает с Python и создана для апологетов Python. Кроме того, приятное свойство PyTorch — построение вычислительного динамического графа, в противовес статическим вычислительным графам, представленным в TensorFlow и Keras. PyTorch сейчас находится на подъеме и используется в разработке Facebook, Twitter, NVIDIA и другими компаниями. Давайте обратимся к туториалу по использованию PyTorch.

Перед вами перевод статьи «A PyTorch tutorial – deep learning in Python», ссылка на оригинал — в подвале статьи.
Первый вопрос для рассмотрения — действительно ли PyTorch лучше TensorFlow? Это субъективно, так как с точки зрения производительности нет больших различий. В любом случае, PyTorch стал серьезным соперником в соревновании между библиотеками глубокого обучения. Давайте начнем изучать библиотеку, оставив для размышлений вопрос о том, что же лучше.
Основы PyTorch
В этом разделе мы обсудим главные идеи, стоящие за PyTorch, начиная с тензоров и вычислительных графов, заканчивая переменными классами и функциональностью автоматического дифференцирования.
Установка на Windows
Стоит сказать, если вы пользователь Windows, на веб-сайте PyTorch нет опции для простой установки библиотеки для этой операционной системы. Однако задача легко решается с помощью этого веб-сайта, где находятся дальнейшие инструкции. Установка стоит затраченных усилий.
Вычислительные графы
Первое, что необходимо понять о любой библиотеке глубокого обучения — идея вычислительных графов. Вычислительный граф — набор вычислений, которые называются узлами (nodes), и которые соединены в прямом порядке вычислений. Другими словами, выбранный узел зависит от узлов на входе, который в свою очередь производит вычисления для других узлов. Ниже представлен простой пример вычислительного графа для вычисления выражения a = (b + c) * (c + 2). Можно разбить вычисление на следующие шаги:
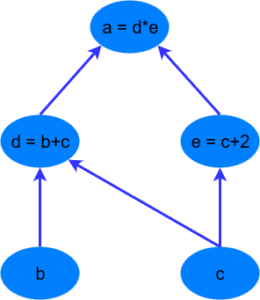
Преимущества использования вычислительного графа в том, что каждый узел является независимым функционирующим куском кода, если получит все необходимые входные данные. Это позволяет оптимизировать производительность при выполнении расчетов, используя многоканальную обработку, параллельные вычисления. Все основные фреймворки для глубокого обучения (TensorFlow, Theano, PyTorch и так далее) включают в себя конструкции вычислительных графов, с помощью которых выполняются операции внутри нейронных сетей и происходит обратное распространение градиента ошибки.
Тензоры
Тензоры — подобные матрице структуры данных, которые являются неотъемлемыми компонентами в библиотеках глубокого обучения и используются для эффективных вычислений. Графические процессоры (GPU) эффективны при вычислении операций между тензорами, что стимулировало волну возможностей в глубоком обучении. В PyTorch тензоры могут определяться несколькими способами:
import torch x = torch.Tensor(2, 3)
Этот код создает тензор размера (2,3), заполненный нулями. В данном примере первое число — количество рядов, второе — количество столбцов:
0 0 0 0 0 0 [torch.FloatTensor of size 2x3]
Мы также можем создать тензор, заполненный случайными float-значениями:
x = torch.rand(2, 3)
Умножение тензоров, сложение друг с другом и другие алгебраические операции просты:
x = torch.ones(2,3) y = torch.ones(2,3) * 2 x + y
Код возвращает:
3 3 3 3 3 3 [torch.FloatTensor of size 2x3]
Также доступна работа с функцией slice в numpy. Например y[:,1]:
y[:,1] = y[:,1] + 1
Которая возвращает:
2 3 2 2 3 2 [torch.FloatTensor of size 2x3]
Теперь вы знаете, как создавать тензоры и работать с ними в PyTorch. Следующим шагом туториала будет обзор более сложных конструкций в библиотеке.
Автоматическое дифференцирование в PyTorch
В библиотеках глубокого обучения есть механизмы вычисления градиента ошибки и обратного распространения ошибки через вычислительный граф. Этот механизм, называемый автоградиентом в PyTorch, легко доступен и интуитивно понятен. Переменный класс — главный компонент автоградиентной системы в PyTorch. Переменный класс обертывает тензор и позволяет автоматически вычислять градиент на тензоре при вызове функции .backward(). Объект содержит данные из тензора, градиент тензора (единожды посчитанный по отношению к некоторому другому значению, потеря) и содержит также ссылку на любую функцию, созданную переменной (если это функция созданная пользователем, ссылка будет пустой).
Создадим переменную из простого тензора:
x = Variable(torch.ones(2, 2) * 2, requires_grad=True)
В объявлении переменной используется двойной тензор размера 2х2 и дополнительно указывается, что переменной необходим градиент. При использовании этой переменной в нейронных сетях, она становится способна к обучению. Если последний параметр будет равен False, то переменная не может использоваться для обучения. В этом простом примере мы ничего не будем тренировать, но хотим запросить градиент для этой переменной, как будет показано ниже.
Далее, создадим новую переменную на основе x.
z = 2 * (x * x) + 5 * x
Чтобы вычислить градиент этой операции по x, dz/dx, можно аналитически получить 4x + 5. Если все элементы x — двойки, то градиент dz/dx — тензор размерности (2,2), заполненный числами 13. Однако сначала необходимо запустить операцию обратного распространения .backwards(), чтобы вычислить градиент относительно чего-либо. В нашем случае инициализируется единичный тензор (2,2), относительно которого считаем градиент. В таком случае вычисление — просто операция d/dx:
z.backward(torch.ones(2, 2)) print(x.grad)
Результатом является следующее:
Variable containing: 13 13 13 13 [torch.FloatTensor of size 2x2]
Заметим, это в точности то, что мы предсказывали вначале. Отметим, градиент хранится в переменной x в свойстве .grad.
Мы научились простейшим операциям с тензорами, переменными и функцией автоградиента в PyTorch. Теперь приступим к написанию простой нейронной сети в PyTorch, которая будет витриной для этих функций в дальнейшем.
Создание нейронной сети в PyTorch
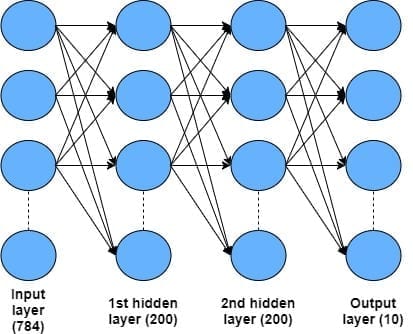
Этот раздел — основной в туториале. Полный код туториала лежит в этом репозитории на GitHub. Здесь мы создадим простую нейронную сеть с 4 слоями, включая входной и два скрытых слоя, для классификации рукописных символов в датасете MNIST. Архитектура, которую мы будем использовать, показана на картинке:

Входной слой состоит из 28 х 28 = 784 пикселей с оттенками серого, которые составляют входные данные в датасете MNIST. Входные данные далее проходят через два скрытых слоя, каждый из которых содержит 200 узлов, использующих линейную выпрямительную функцию активации (ReLU). Наконец, мы имеем выходной слой с десятью узлами, соответствующими десяти рукописным цифрам от 0 до 9. Для такой задачи классификации будем использовать выходной softmax-слой.
Класс для построения нейронной сети
Чтобы создать нейронную сеть в PyTorch, используется класс nn.Module. Чтобы им воспользоваться, необходимо наследование, что позволит использовать весь функционал базового класса nn.Module, но при этом еще имеется возможность переписать базовый класс для конструирования модели или прямого прохождения через сеть. Представленный ниже код поможет объяснить сказанное:
import torch.nn as nn import torch.nn.functional as F class Net(nn.Module): def __init__(self): super(Net, self).__init__() self.fc1 = nn.Linear(28 * 28, 200) self.fc2 = nn.Linear(200, 200) self.fc3 = nn.Linear(200, 10)
В таком определении можно видеть наследование базового класса nn.Module. В первой строке инициализации класса def __init__(self) мы имеем требуемую super() функцию языка Python, которая создает объект базового класса. В следующих трех строках создаем полностью соединенные слои как показано на диаграмме архитектуры. Полностью соединенный слой нейронной сети представлен объектом nn.Linear, в котором первый аргумент — определение количества узлов в i-том слое, а второй — количество узлов в i+1 слое. Из кода видно, первый слой принимает на входе 28×28 пикселей и соединяется с первым скрытым слоем с 200 узлами. Далее идет соединение с другим скрытым слоем с 200 узлами. И, наконец, соединение последнего скрытого слоя с выходным слоем с 10 узлами.
После определения скелета архитектуры сети, необходимо задать принципы, по которым данные будут перемещаться по ней. Это делается с помощью определяемого метода forward(), который переписывает фиктивный метод в базовом классе и требует определения для каждой сети:
def forward(self, x): x = F.relu(self.fc1(x)) x = F.relu(self.fc2(x)) x = self.fc3(x) return F.log_softmax(x)
Для метода forward() берем входные данные x в качестве основного аргумента. Далее, загружаем всё в в первый полностью соединенный слой self.fc1(x) и применяем активационную функцию ReLU для узлов в этом слое, используя F.relu(). Из-за иерархической природы этой нейронной сети, заменяем x на каждой стадии и отправляем на следующий слой. Делаем эту процедуру на трех соединенных слоях, за исключением последнего. На последнем слое возвращаем не ReLU, а логарифмическую softmax активационную функцию. Это, в комбинации с функцией потери отрицательного логарифмического правдоподобия, дает многоклассовую на основе кросс-энтропии функцию потерь, которую мы будет использовать для тренировки сети.
Мы определили нейронную сеть. Следующим шагом будет создание экземпляра (instance) этой архитектуры:
net = Net() print(net)
При выводе экземпляра класса Net получаем следующее:
Net ( (fc1): Linear (784 -> 200) (fc2): Linear (200 -> 200) (fc3): Linear (200 -> 10) )
Что очень удобно, так как подтверждает структуру нашей нейронной сети.
Тренировка сети
Далее необходимо задать метод оптимизации и критерий качества:
# Осуществляем оптимизацию путем стохастического градиентного спуска optimizer = optim.SGD(net.parameters(), lr=learning_rate, momentum=0.9) # Создаем функцию потерь criterion = nn.NLLLoss()
В первой строке создаем оптимизатор на основе стохастического градиентного спуска, устанавливая скорость обучения (learning rate; в нашем случае определим этот показатель на уровне 0.01) и momentum. Еще в оптимизаторе необходимо определить все остальные параметры сети, но это делается легко в PyTorch благодаря методу .parameters() в базовом классе nn.Module, который наследуется из него в новый класс Net.
Далее устанавливается метрика контроля качества — функция потерь отрицательного логарифмического правдоподобия. Такой вид функции в комбинации с логарифмической softmax-функцией на выходе нейронной сети дает эквивалентную кросс-энтропийную потерю для 10 классов задачи классификации.
Настало время тренировать нейронную сеть. Во время тренировки данные будут извлекаться из объекта загрузки данных, который включен в модуль PyTorch. Здесь не будут рассмотрены детали этого способа, но вы можете найти код в этом репозитории на GitHub. Из загрузчика будут поступать партиями входные и целевые данные, которые будут подаваться в нашу нейронную сеть и функцию потерь, соответственно. Ниже представлен полный код для тренировки:
# запускаем главный тренировочный цикл
for epoch in range(epochs):
for batch_idx, (data, target) in enumerate(train_loader):
data, target = Variable(data), Variable(target)
# изменим размер с (batch_size, 1, 28, 28) на (batch_size, 28*28)
data = data.view(-1, 28*28)
optimizer.zero_grad()
net_out = net(data)
loss = criterion(net_out, target)
loss.backward()
optimizer.step()
if batch_idx % log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.data[0]))
Внешний тренировочный цикл проходит по количеству эпох, а внутренний тренировочный цикл проходит через все тренировочные данные в партиях, размер которых задается в коде как batch_size. На следующей линии конвертируем данные и целевую переменную в переменные PyTorch. Входной датасет MNIST, который находится в пакете torchvision (который вам необходимо установить при помощи pip), имеет размер (batch_size, 1, 28, 28) при извлечении из загрузчика данных. Такой четырехмерный тензор больше подходит для архитектуры сверточной нейронной сети, чем для нашей полностью соединенной сети. Тем не менее, необходимо уменьшить размерность данных с (1,28,28) до одномерного случая для 28 х 28 = 784 входных узла.
Функция .view() работает с переменными PyTorch и преобразует их форму. Если мы точно не знаем размерность данного измерения, можно использовать ‘-1’ нотацию в определении размера. Поэтому при использование data.view(-1,28*28) можно сказать, что второе измерение должно быть равно 28 x 28, а первое измерение должно быть вычислено из размера переменной оригинальных данных. На практике это означает, что данные теперь будут размера (batch_size, 784). Мы можем пропустить эту партию входных данных в нашу нейросеть, и магический PyTorch сделает за нас тяжелую работу, эффективно выполняя необходимые вычисления с тензорами.
В следующей строке запускаем optimizer.zero_grad(), который обнуляет или перезапускает градиенты в модели так, что они готовы для дальнейшего обратного распространения. В других библиотеках это реализовано неявно, но нужно помнить, что в PyTorch это делается явно. Давайте рассмотрим следующий код:
net_out = net(data) loss = criterion(net_out, target)
Первая строка, в которой подаем порцию данных на вход нашей модели, вызывает метод forward() в классе Net. После запуска строки переменная net_out будет иметь логарифмический softmax-выход из нашей нейронной сети для заданной партии данных. Это одна из самых замечательных особенностей PyTorch, так как можно активировать любой стандартный отладчик Python, который вы обычно используете, и мгновенно узнать, что происходит в нейронной сети. Это противоположно другим библиотекам глубокого обучения, TensorFlow и Keras, в которых требуется производить сложные отладочные действия, чтобы узнать, что ваша нейронная сеть действительно создает. Надеюсь, вы поиграете с кодом для этого туториала и поймете, насколько в PyTorch удобный отладчик.
Во второй строке кода инициализируется функция потери отрицательного логарифмического правдоподобия между выходом нашей нейросети и истинными метками заданной партии данных.
Давайте посмотрим на следующие две строки:
loss.backward() optimizer.step()
Первая строка запускает операцию обратного распространения ошибки из переменной потери в обратном направлении через нейросеть. Если сравнить это с упомянутой выше операцией .backward(), которую мы рассматривали в туториале, видно, что не используется никакой аргумент в операции .backward(). Скалярные переменные при использовании на них .backward() не требуют аргумента; только тензорам необходим согласованный аргумент для передачи в операцию .backward().
В следующей строке мы просим PyTorch выполнить градиентный спуск по шагам на основе вычисленных во время операции .backward() градиентов.
Наконец, будем выводить результаты каждый раз, когда модель достигает определенного числа итераций:
if batch_idx % log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.data[0]))
Эта функция выводит наш прогресс на протяжении эпох тренировки и показывает ошибку нейросети в этот момент. Отметим, что доступ к потерям находится в свойстве .data у переменной PyTorch, которая в данном случае будет массивом с единственным значением. Получаем скалярную потерю используя loss.data[0].
Запуская этот тренировочный цикл, получаем на выходе следующее:
Train Epoch: 9 [52000/60000 (87%)] Loss: 0.015086 Train Epoch: 9 [52000/60000 (87%)] Loss: 0.015086 Train Epoch: 9 [54000/60000 (90%)] Loss: 0.030631 Train Epoch: 9 [56000/60000 (93%)] Loss: 0.052631 Train Epoch: 9 [58000/60000 (97%)] Loss: 0.052678
После 10 эпох, значение потери по величине должно получиться меньше 0.05.
Тестирование сети
Чтобы проверить нашу обученную нейронную сеть на тестовом датасете MNIST, запустим следующий код:
test_loss = 0
correct = 0
for data, target in test_loader:
data, target = Variable(data, volatile=True), Variable(target)
data = data.view(-1, 28 * 28)
net_out = net(data)
# Суммируем потери со всех партий
test_loss += criterion(net_out, target).data[0]
pred = net_out.data.max(1)[1] # получаем индекс максимального значения
correct += pred.eq(target.data).sum()
test_loss /= len(test_loader.dataset)
print('nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
Этот цикл совпадает с тренировочным циклом до строки test_loss. Здесь мы извлекаем потери сети используя свойство .data[0] как и раньше, но только все в одной строке. Далее в строке pred используется метод data.max(1), который возвращает индекс наибольшего значения в определенном измерении тензора. Теперь выход нашей нейронной сети будет иметь размер (batch_size, 10), где каждое значение из второго измерения длины 10 — логарифмическая вероятность, которую нейросеть приписывает каждому выходному классу (то есть это логарифмическая вероятность принадлежности картинки к символу от 0 до 9). Поэтому для каждого входного образца в партии net_out.data будет выглядеть следующим образом:
[-1.3106e+01, -1.6731e+01, -1.1728e+01, -1.1995e+01, -1.5886e+01, -1.7700e+01, -2.4950e+01, -5.9817e-04, -1.3334e+01, -7.4527e+00]
Значение с наибольшей логарифмической вероятностью — цифра от 0 до 9, которую нейронная сеть распознает на входной картинке. Иначе говоря, это лучшее предсказание для заданного входного объекта. В примере net_out.data таким лучшим предсказанием является значение -5.9817e-04, которое соответствует цифре “7”. Поэтому для этого примера нейросеть предскажет знак “7”. Функция .max(1) определяет это максимальное значение во втором пространстве (если мы хотим найти максимум в первом пространстве, мы должны аргумент функции изменить с 1 на 0) и возвращает сразу и максимальное найденное значение, и индекс ему соответствующий. Поэтому эта конструкция имеет размер (batch_size, 2). В данном случае, нас интересует индекс максимального найденного значения, к которому мы получаем доступ с помощью вызова .max(1)[1].
Теперь у нас есть предсказание нейронной сети для каждого примера в определенной партии входных данных, и можно сравнить его с настоящей меткой класса из тренировочного датасета. Это используется для подсчета количества правильных ответов. Чтобы сделать это в PyTorch, необходимо воспользоваться функцией .eq(), которая сравнивает значения в двух тензорах и при совпадении возвращает единицу. В противном случае, функция возвращает 0:
correct += pred.eq(target.data).sum()
Суммируя выходы функции .eq(), получаем счетчик количества раз, когда нейронная сеть выдает правильный ответ. По накопленной сумме правильных предсказаний можно определить общую точность сети на тренировочном датасете. Наконец, проходя по каждой партии входных данных, выводим среднее значение функции потери и точность модели:
test_loss /= len(test_loader.dataset)
print('nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
После тренировки сети за 10 эпох получаем следующие результаты на тестовой выборке:
Test set: Average loss: 0.0003, Accuracy: 9783/10000 (98%)
Мы получили точность 98%. Весьма неплохо!
В туториале рассмотрены базовые принципы PyTorch, начиная c тензоров до функции автоматического дифференцирования (autograd) и заканчивая пошаговым руководством, как создать полностью соединенную нейронную сеть при помощи nn.Module.
Интересные статьи:





Python 3.9.1 (tags/v3.9.1:1e5d33e, Dec 7 2020, 17:08:21) [MSC v.1927 64 bit (AMD64)] on win32 Type «help», «copyright», «credits» or «license» for more information. >>> import torch Traceback (most recent call… Подробнее »
надо ёпт прописывать все параметры!!
даже количество эпох не указали
тут все — https://github.com/adventuresinML/adventures-in-ml-code/blob/master/pytorch_nn.py