PyTorch / Нейросети и глубокое обучение

Microsoft ViSNet: предсказание активности молекул

3 марта 2024

Microsoft ViSNet: предсказание активности молекул

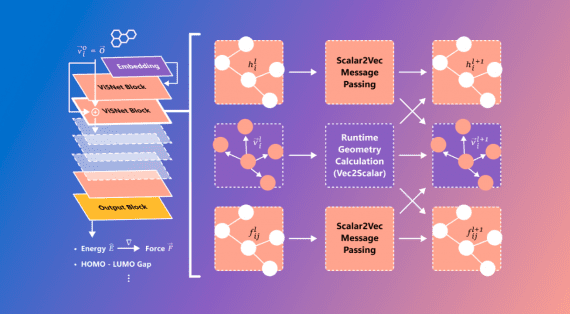
Microsoft опубликовала ViSNet – графовую нейросеть, моделирующую геометрию сложных молекул для предсказания их активности. ViSNet может значительно ускорить поиск и изучение новых лекарств. Моделирование молекулярной геометрии позволяет предсказывать, как молекулярные…

PyTorch-LifeStream: библиотека Сбера для обработки событийных данных

5 февраля 2022

PyTorch-LifeStream: библиотека Сбера для обработки событийных данных

Сбер опубликовал в открытом доступе PyTorch-Lifestream — библиотеку алгоритмов построения векторных представлений событийных данных. Библиотека позволяет обрабатывать терабайтные объемы таких данных, как банковские транзакции, игровые события и истории покупок. Библиотека…

Невидимая клавиатура для смартфонов на основе декодеров

18 сентября 2021

Невидимая клавиатура для смартфонов на основе декодеров

Ученые разработали модель, позволяющую вводить текст на смартфонах на основе памяти пользователя о расположении букв в раскладке клавиатуры. Такая клавиатура позволяет набирать текст на 160% быстрее, чем при использовании экранной…

PyTorch-плагин Amazon для прямого доступа к датасетам S3

13 сентября 2021

PyTorch-плагин Amazon для прямого доступа к датасетам S3

Amazon выпустила open-source плагин для PyTorch, предназначенный для получения доступа к датасетам, хранящимся в Amazon Simple Storage Service (S3). Плагин позволяет в потоковом режиме манипулировать датасетами любого размера, устраняя необходимость…

Новый метод переноса стиля ArtFlow позволяет выполнять стилизацию изображений без потерь

12 апреля 2021

Новый метод переноса стиля ArtFlow позволяет выполнять стилизацию изображений без потерь

ArtFlow — это фреймворк для переноса стиля изображения без потерь с помощью обратимых нейронных потоков. Код в открытом доступе на Github. Зачем это нужно Задача универсального переноса стиля (UST) позволяет…

GraphGallery: библиотека для графовых нейросетей на PyTorch и TensorFlow

2 марта 2021

GraphGallery: библиотека для графовых нейросетей на PyTorch и TensorFlow

GraphGallery — это библиотека для обучения и тестирований графовых нейросетей. В GraphGallery реализованы состязательные атаки на графовые нейросети. Библиотека совместима с PyTorch, TensorFlow 2.x, Pytorch Geometric (PyG) и Deep Graph Library (DGL).…

FaceX-Zoo: библиотека на PyTorch для распознавания лица на изображении

29 января 2021

FaceX-Zoo: библиотека на PyTorch для распознавания лица на изображении

FaceX-Zoo — это открытая библиотека на PyTorch для распознавания лица на изображениях. Библиотека предоставляет модуль для обучения моделей с разными конфигурациями функционала ошибки и базовой архитектуры. Кроме того, в FaceX-Zoo…

PyTorch 1.3: квантизация, перенос модели на мобильные устройства и именованные тензоры

16 октября 2019

PyTorch 1.3: квантизация, перенос модели на мобильные устройства и именованные тензоры

В новой версии PyTorch появился функционал для квантизации, переноса модели на мобильные устройства и именованных тензоров. Квантизация — это метод уменьшения размера обученной нейросети. Помимо этого, для PyTorch опубликовали библиотеки…

CrypTen: инструмент для обучения моделей на зашифрованных данных

15 октября 2019

CrypTen: инструмент для обучения моделей на зашифрованных данных

CrypTen — это обертка над PyTorch для обучения нейросетевых моделей на зашифрованных данных. Это снимает ограничения в использовании PyTorch в задачах, где секретность данных приоритетна. Несмотря на прогресс в обучении…

NVIDIA выпустили обертку над PyTorch для обучения моделей

16 сентября 2019

NVIDIA выпустили обертку над PyTorch для обучения моделей

Neural Modules (NeMo) — это библиотека от NVIDIA для обучения нейросетевых моделей. NeMo основана на PyTorch. NeMo делится на коллекции моделей для задач из отдельных сфер. Сейчас доступны две коллекции:…

Обновления: PyTorch 1.2, torchtext 0.4, torchaudio 0.3 и torchvision 0.4

14 августа 2019

Обновления: PyTorch 1.2, torchtext 0.4, torchaudio 0.3 и torchvision 0.4

Вышли обновления для библиотеки PyTorch и дополнительных библиотек для обработки текста, аудио и изображений. В PyTorch добавился модуль с трансформером, в torchaudio — новые способы трансформации и стандартизации аудиоданных, в…

Как конвертировать модель из TensorFlow в PyTorch

13 августа 2019

Как конвертировать модель из TensorFlow в PyTorch

Разработчики из HuggingFace опубликовали тьюториал по конвертированию предобученных моделей из TensorFlow в PyTorch. Это может пригодиться при попытке внедрить предобученную модель на TF в пайплайн на PyTorch. В качестве примера…

PyTorch Hub: база предобученных моделей на PyTorch

14 июня 2019

PyTorch Hub: база предобученных моделей на PyTorch

PyTorch Hub — это открытая база с предобученными нейросетевыми моделями на PyTorch. Сейчас в базе 19 моделей, в том числе для задач компьютерного зрения и обработки естественного языка. PyTorch Hub…

Pytorch выпустили обновление библиотеки для компьютерного зрения torchvision 0.3

26 мая 2019

Pytorch выпустили обновление библиотеки для компьютерного зрения torchvision 0.3

Библиотека torchvision с инструментами для компьютерного зрения на Pytorch обновилась до версии 0.3. В обновленной версии был расширен список доступных моделей для распознавания объектов, семантической/instance сегментаций и распознавания опорных точек…

FAIR представила фреймворк PyTorch BigGraph

4 апреля 2019

FAIR представила фреймворк PyTorch BigGraph

На конференции SysML представлен PyTorch BigGraph (PBG) — распределенную систему для обучения векторного представления графов. Особенность этой системы в том, что она рассчитана на большие графы, содержащие до миллиардов вершин…

PyTorch или TensorFlow в 2026 году: отличия, сравнение кода и что выбрать

11 января 2019

PyTorch или TensorFlow в 2026 году: отличия, сравнение кода и что выбрать

Статья полностью обновлена в октябре 2026 года. Первая версия 2019 года была переводом сравнения Кирилла Добовикова «PyTorch vs TensorFlow — spotting the difference»; что изменилось с тех пор, мы собрали…

Эпоха, батч, итерация — в чем различия?

26 декабря 2018

Эпоха, батч, итерация — в чем различия?

Вам должны быть знакомы моменты, когда вы смотрите на код и удивляетесь: “Почему я использую в коде эти три параметра, в чем отличие между ними?”. И это неспроста, так как…

Функции активации нейросети: сигмоида, линейная, ступенчатая, ReLu, tahn

26 ноября 2018

Функции активации нейросети: сигмоида, линейная, ступенчатая, ReLu, tahn

Что делает искусственный нейрон? Простыми словами, он считает взвешенную сумму на своих входах, добавляет смещение (bias) и решает, следует это значение исключать или использовать дальше (да, функция активации так и…

Метод обратного распространения ошибки: математика, примеры, код

24 ноября 2018

Метод обратного распространения ошибки: математика, примеры, код

Обратное распространение ошибки — это способ обучения нейронной сети. Цели обратного распространения просты: отрегулировать каждый вес пропорционально тому, насколько он способствует общей ошибке. Если мы будем итеративно уменьшать ошибку каждого веса, в…

VGG16 — нейросеть для выделения признаков изображений

23 ноября 2018

VGG16 — нейросеть для выделения признаков изображений

VGG16 — модель сверточной нейронной сети, предложенная K. Simonyan и A. Zisserman из Оксфордского университета в статье “Very Deep Convolutional Networks for Large-Scale Image Recognition”. Модель достигает точности 92.7% —…