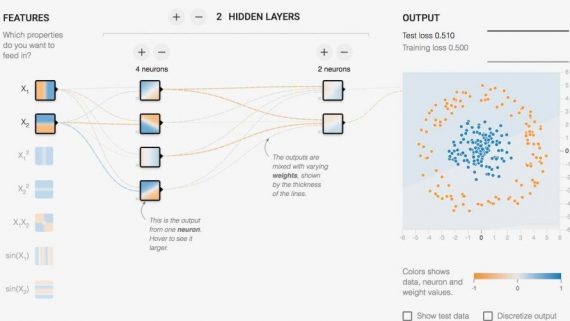
С помощью новой библиотеки TensorNetworks от GoogleAI стало общедоступным использование тензорных сетей, которые играют большую роль в современной квантовой физике. Однако, помимо применения в квантовых системах, тензорные сети все чаще находят применение в машинном обучении. Библиотека была разработана в сотрудничестве с институтом теоретической физики Периметр и компании X. TensorNetwork использует TensorFlow в качестве движка и оптимизирован для GPU. Это может позволяет ускорить вычисления до 100x по сравнению с вычислениями на CPU.
Тензорные сети обеспечивают эффективное приближение к определенным классам квантовых состояний, а связанный с ними графический язык упрощает описание и наглядное представление о квантовых схемах, каналах, протоколах, открытых системах и многом другом. Они позволяют сосредоточиться на квантовых состояниях, которые наиболее актуальны для реальных проблем, к примеру, на состояниях с низкой энергией, игнорируя при этом другие состояния.
Разработчики библиотеки представили ее работу в двух статьях. В первой статье представлен API библиотеки и обзор тензорных сетей для аудитории, не относящейся к физикам. Во второй статье представлен конкретный случай использования в физике, демонстрируя ускорение, получаемое при использовании GPU.
Что такое тензорные сети?
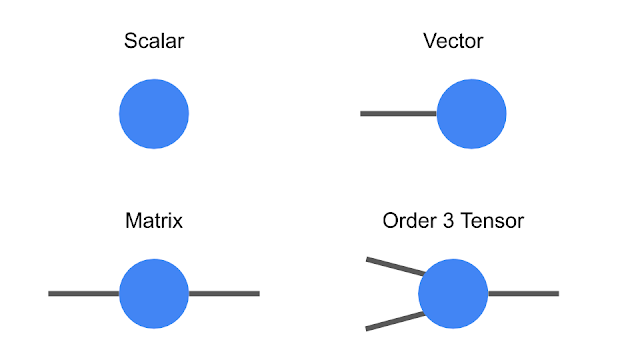
Тензоры — это многомерные массивы, классифицированные по иерархии в соответствии с их порядком: например, обычное число — это тензор нулевого порядка (также известный как скаляр), вектор — тензор первого порядка, матрица — тензор второго порядка, и так далее. В то время как тензоры низкого порядка легко могут быть представлены явным массивом чисел или математическим символом, таким как Tijnklm(где число индексов представляет порядок тензора), эта запись становится очень громоздкой, когда мы начинаем говорить о тензорах высокого порядка. В этот момент полезно начать использовать схематическое обозначение, где просто рисуется круг (или какая-либо другая фигура) с количеством линий или ножек, выходящих из него — количество ножек совпадает с порядком тензора. В этих обозначениях скаляр — это просто круг, вектор имеет один выход, матрица — два выхода и т.д. Каждая ветвь тензора также имеет размерность, равную размерности этой ножки (этого измерения). Например, вектор, представляющий скорость объекта в пространстве, будет трехмерным тензором первого порядка. Преимущество представления тензоров таким способом заключается в кратком кодировании математических операций, например, умножении матрицы на вектор для создания другого вектора или умножении двух векторов на скаляр.
Тензорные сети на практике
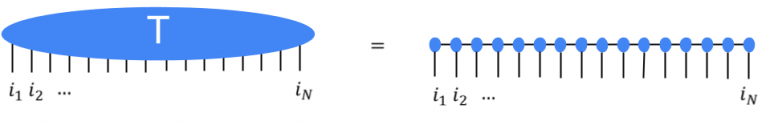
Рассмотрим коллекцию черно-белых изображений, каждое из которых можно рассматривать как список значений N пикселей. Один пиксель одного изображения может быть закодирован в двумерный вектор, и, комбинируя эти коды пикселей вместе, мы можем создать 2N -мерное кодирование всего изображения. Мы можем преобразовать этот многомерный вектор в N—мерный тензор, а затем сложим все тензоры в нашей коллекции изображений, чтобы получить полный тензор Ti1, i2, …, iN.
Это очень затратно: кодирование изображений примерно с 50 пикселями уже заняло бы петабайты памяти. Вот где приходят на помощь тензорные сети. Вместо того, чтобы непосредственно сохранять или манипулировать тензором T, мы вместо этого представляем T как сжатие множества меньших составляющих тензоров в форме тензорной сети. Это оказывается намного более эффективно. Например, популярная сеть Matrix Product State (MPS) будет описывать T, как N намного меньших тензоров, так что общее число параметров будет только линейным по N, а не экспоненциальным.
Не очевидно, что большие тензорные сети можно эффективно использовать, при этом избегая необходимости в огромном объеме памяти. Но оказывается, что во многих случаях это возможно, поэтому тензорные сети широко используются в квантовой физике, а теперь и в машинном обучении. Стоуденмир и Шваб использовали только что описанное кодирование для создания модели классификации изображений, демонстрируя новое использование тензорных сетей. Библиотека TensorNetwork разработана для облегчения именно такой работы.
Производительность при использовании в физике
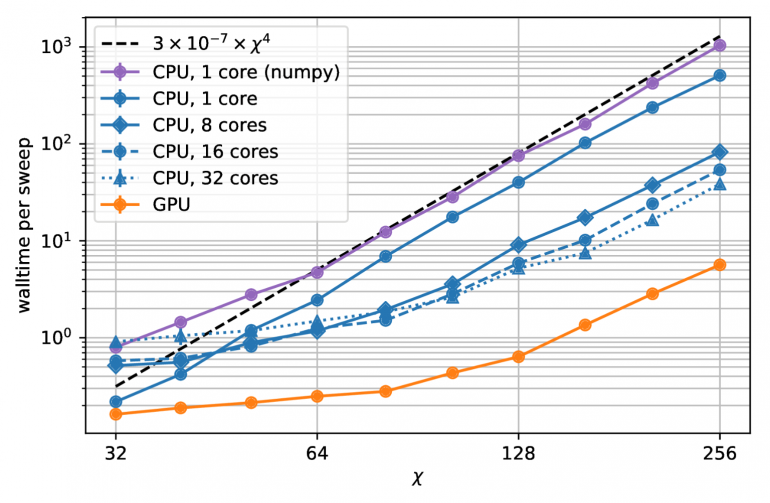
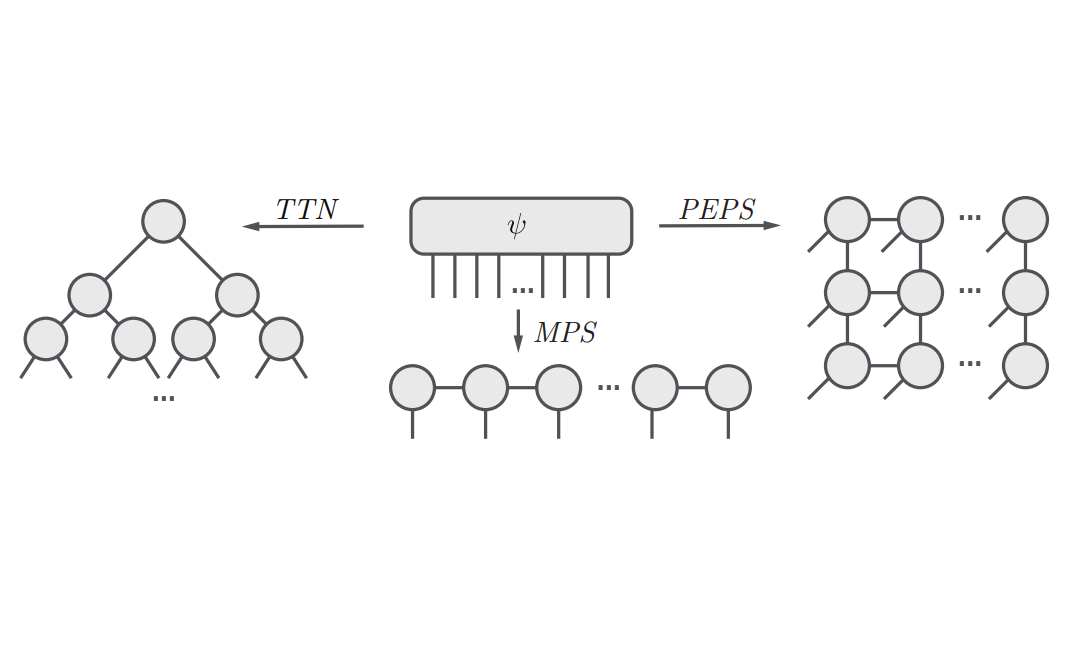
Аппроксимация квантовых состояний является типичным вариантом использования тензорных сетей в физике и хорошо подходит для иллюстрации возможностей библиотеки TensorNetwork. Во второй статье разработчиками описан алгоритм древовидной тензорной сети (TTN) для аппроксимации основного состояния периодической квантовой спиновой цепочки (1D) или решеточной модели на тонком торе (2D) и реализуем алгоритм с использованием TensorNetwork. При сравнении использования CPU и GPU, наблюдается значительное ускорение вычислений, вплоть до 100 раз, при использовании GPU и библиотеки TensorNetwork.