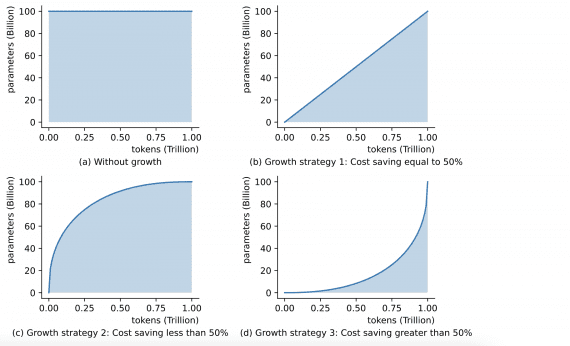
В Google предложили модифицированную логистическую функцию ошибки (Bi-Tempered Logistic Loss), которая устойчива к шумным данным. Качество ML-моделей напрямую зависит от качества данных, на которых они обучались. Данные из реального мира обычно содержат шум, который мешает модели учиться. Шум в данных может быть нескольких видов: от поврежденных объектов в выборке (например, вспышка на изображении кота) до неверно размеченных примеров (например, изображение кота размечено как «собака»).
Возможность модели учитывать шумные данные при обучении зависит от той функции потерь, которая используется. Для задачи классификации стандартной функцией потерь является логистическая функция ошибки. Однако она неудачно справляется с шумными данными по двум причинам:
- Логистическая функция потерь неустойчива к выбросам в данных. Единственный сильно отличный от остальных примеров объект может сместить границу принятия решения (decision boundary);
- Неверно размеченные примеры, близко расположенные к верным, могут растянуть границу принятия решения у классификатора. Генерализующая способность классификатора также ухудшится
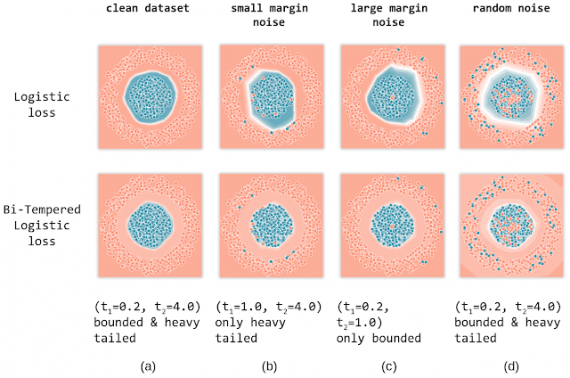
В Google предложили модифицированную логистическую функцию потерь, которая учитывает эти недостатки стандартной формулировки функции. Модифицированная функция называется Bi-Tempered Logistic Loss. Функция имеет два обучаемых параметра, каждый из которых отвечает за один из типов шумных данных. Исследователи называют их “температурами”: t1 характеризует ограниченность функции, а t2 характеризует то, насколько длинный хвост у распределения данных.

Тестирование
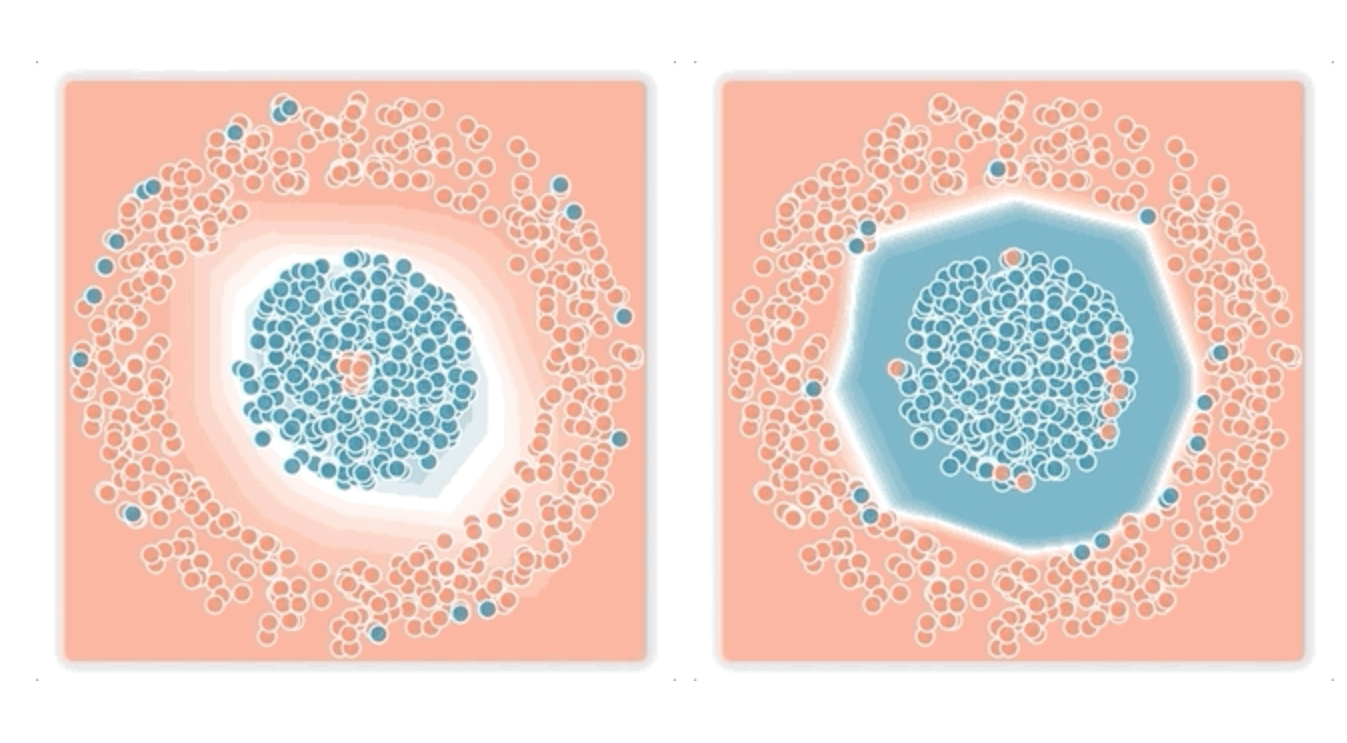
Чтобы продемонстрировать разницу в использовании стандартной формулировки Logistic Loss и Bi-Tempered Logistic Loss при обучении модели. Исследователи обучили двухслойную полносвязную нейросеть для задачи бинарной классификации. Данные для обучения были сгенерированы. Ниже видно, что Bi-Tempered Logistic Loss более точна в определении границ для данных разной степени зашумленности.