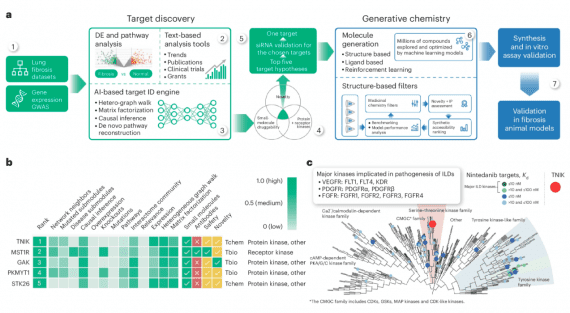
Исследовательская команда Microsoft Research представила On-Policy RL with Optimal reward baseline (OPO) — упрощенный алгоритм обучения с подкреплением для выравнивания больших языковых моделей. Новый метод решает ключевые проблемы современных RLHF алгоритмов: нестабильность обучения из-за слабых on-policy ограничений и вычислительную неэффективность из-за вспомогательных моделей. Код реализации метода выложен на Github.
Проблемы современных RLHF алгоритмов
Обучение с подкреплением на основе человеческой обратной связи (RLHF) — основополагающий подход для выравнивания больших языковых моделей с человеческими предпочтениями. Стандартный пайплайн RLHF обычно включает контролируемое дообучение с последующим обучением с подкреплением, часто использующим алгоритм Proximal Policy Optimization (PPO), управляемый обученной моделью вознаграждения.
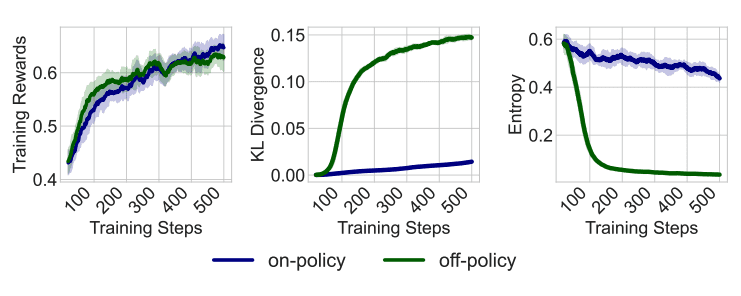
Современные RLHF алгоритмы сталкиваются с серьезными вызовами в стабильности и эффективности. PPO требует обучения дополнительной модели ценности для оценки преимуществ, что создает дополнительные вычислительные затраты. Методы часто подвержены нестабильности из-за слабых on-policy ограничений. On-policy принцип означает, что градиенты политики должны вычисляться на данных, собранных именно текущей политикой, то есть формулой вероятностного распределения, которую модель назначает разным возможным ответам y для данного входа x. Слабые on-policy ограничения приводят к нарушению этого принципа — использованию данных от предыдущих версий политики, что технически делает обучение off-policy. В результате модель начинает генерировать очень похожие, однообразные ответы, слишком резко меняет свое поведение между обновлениями и даже ухудшает свои исходные способности.
Ключевые инновации OPO
Строгое on-policy обучение
OPO использует строгое on-policy обучение, которое эмпирически стабилизирует процесс обучения и значительно повышает возможности исследования. В отличие от PPO, который собирает батч данных с текущей политикой и затем выполняет множественные обновления градиентов на этом фиксированном батче, строгое on-policy обучение гарантирует, что каждый шаг градиента вычисляется с использованием свежих данных, сэмплированных с текущей политики.
Это контрастирует с обычными policy gradient, которые вводят расхождение off-policy при повторных прогонах. На практике это может способствовать коллапсу энтропии выборки и большим сдвигам политики, что требует явной энтропийной регуляризации.
Оптимальный reward baseline
Команда разработала математически оптимальный бейзлайн, который теоретически минимизирует дисперсию градиента. Идея заключается в том, чтобы вычитать из каждой награды специальное опорное значение, которое не влияет на направление обучения, но делает процесс более стабильным.
Оптимальный бейзлайн b* вычисляется по формуле:
b* = E[||∇θ log πθ(y|x)||² · r(x,y)] / E[||∇θ log πθ(y|x)||²]Это взвешенное среднее наград, где весами служат квадраты градиентов модели.
Упрощение для генерации текста
Для языковых задач можно использовать более простую формулу. Исследователи предположили, что влияние каждого слова на обучение примерно одинаково, поэтому общее влияние ответа пропорционально его длине. В результате формула оптимального бейзлайна упрощается до:
b* = E[ly · r(x,y)] / E[ly]где ly — длина ответа y в токенах.
Таким образом, более длинные ответы получают больший вес при расчете. Это означает, что качество длинных ответов сильнее влияет на то, что модель считает «нормальным» уровнем производительности.
Экспериментальные результаты
Исследователи протестировали алгоритм на модели DeepSeek-R1-Distill-Qwen-7B, используя математический подраздел из Skywork-OR1-RL-Data (48 тысяч задач). Применялась простая функция награды: 1 за правильный ответ, 0 за неправильный. Производительность оценивалась на трех математических бенчмарках: MATH-500, AIME 2024 и AIME 2025.
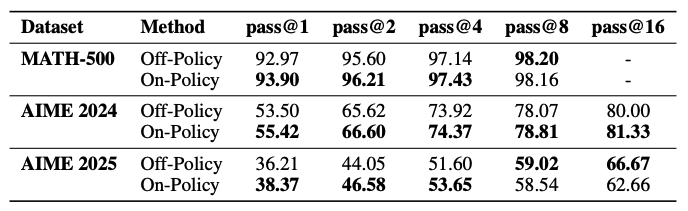
Строгое on-policy обучение значительно превосходит обучение off-policy по метрике прохождения@1 на всех тестах. Например, на AIME 2024 строгий подход показал 55.42% против 53.50% у обучения off-policy.
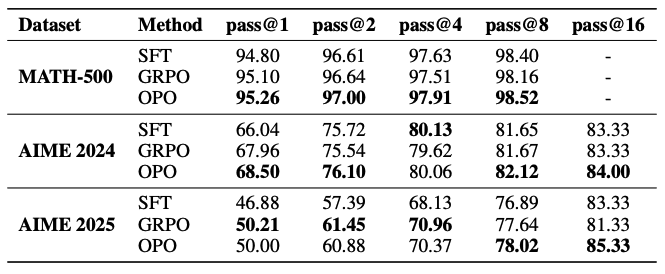
Алгоритм с OPO превосходит групповую относительную оптимизацию (GRPO) в большинстве случаев. На MATH-500 OPO достиг 95.26% прохождения@1 против 95.10% у GRPO. Преимущества особенно заметны когда модели дается несколько попыток для решения задачи: на AIME 2025 при 16 попытках алгоритм достиг 85.33% успешности против 81.33% у групповой относительной оптимизации.
Дополнительные преимущества
Алгоритм генерирует более разнообразные и менее повторяющиеся ответы, поддерживая при этом более стабильную динамику обучения с более низкой расходимостью Кульбака-Лейблера и более высокой энтропией выходных данных по сравнению с существующими методами.