Исследователи из DeepMind открыли доступ к датасету математических задач и ответов к ним и проверили то, как существующие архитектуры справляются с предсказанием ответа на математическую задачу. В будущем это может помочь обучать модели для решения задач, у которых до сих пор нет решения.
Ученые ставят перед собой первоначальную цель обучить нейросеть тем навыкам, которые используют люди при решении математических задач:
- Распознавание сущностей (entity recognition) чисел, арифметических операций, переменных и слов, описывающих условия задачи;
- Планирование порядка решения задачи;
- Запоминание промежуточных переменных в случае с композициями функций (например, h(f(x)));
- Применение аксиом, правил подстановки и др.
Сам датасет представляет собой набор из математических вопросов и ответов на них. Темы вопросов, освещенные в датасете, охватывают школьную программу.

Сравнение архитектур
В рамках экспериментов исследователи посмотрели, как с задачей справляются простые LSTM и RMC, LSTM и RMC с attention слоем и Трансформер. В качестве метрик эффективности были выбраны интерполяция и экстраполяция.
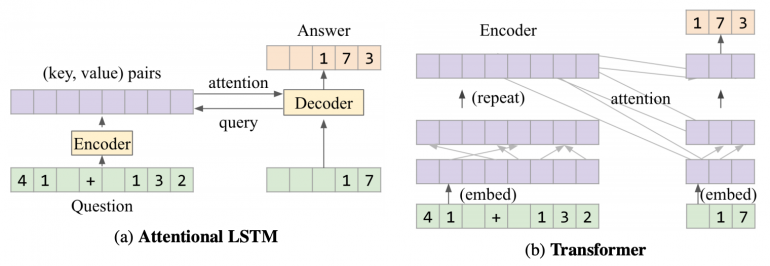
LSTM показали себя лучше, чем RMC. Наилучшие результаты показал Трансформер, добавление attention слоя не повысило метрику экстраполяции LSTM:
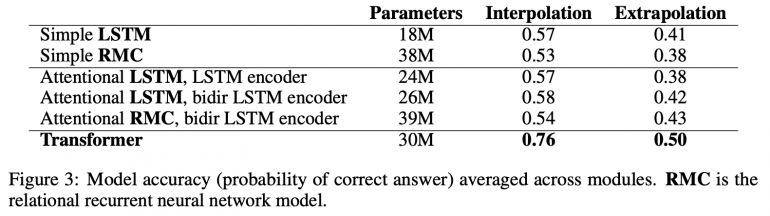
Результаты
LSTM или RMC
Использование RMC с более чем 1 слотом памяти не приводило к повышению эффективности модели. Также, RMC были менее ресурсозатратные в контексте расходования памяти, но обучались дольше LSTM.
Добавлять ли attention?
LSTM с attention слоем и без имели схожую эффективность. Проблема может быть в том, что LSTM с attention слоем не может распарсить сам вопрос, в связи возможность переключать внимание с одного скрытого слоя на другой оказывается бесполезной.
Простые виды вопросов для нейросетей
Меньшую сложность у моделей вызывали вопросы, касающиеся округления чисел, сравнения чисел и поиска неизвестной переменной в выражении. В то же самое время среди наиболее сложных задач была факторизация (разложение числа на множители).
Подробности экспериментов и более подробные выводы опубликованы в статье.
Направления будущих исследований
Исследователи планируют в дальнейшем включить в датасет графические геометрические задачи, а также расширить вариативность описания задач одного типа. На данный момент в датасете описания задач одного типа представлены в схожем формате, что ограничивает способность к генерализации у моделей, обученных на этом сете данных.