Вариационный автоэнкодер (Variational Autoencoder – VAE) — генеративная модель, которая находит применение во многих областях исследований: от генерации новых человеческих лиц до создания полностью искусственной музыки, в противоположность использованию нейросетей в качестве регрессоров или классификаторов.
Эта статья рассказывает о том, что такое вариационный автоэнкодер, почему это архитектура стала так популярна, и почему VAE используют в качестве генеративного инструмента почти во всех областях цифрового медиа-пространства.
Прежде всего, зачем нужен вариационный автоэнкодер?
Генеративные модели используют для того, чтобы производить случайные выходные данные, которые выглядят схоже с тренировочным набором данных, и тоже самое вы можете делать с помощью VAEs. Однако зачастую необходимо изменить или исследовать вариации на данных, которые уже имеются, и не случайным образом, а определённым желаемым способом. В этом случае VAEs работают лучше, чем любой другой ныне доступный метод.
Нейросеть автоэнкодера на самом деле является парой из двух соединенных нейросетей – энкодера и декодера. Энкодер принимает входные данные и преобразует их, делая представление более компактным и сжатым. В свою очередь, декодер использует преобразованные данные для трансформации их обратно в оригинальное состояние.
В случае, если вы незнакомы с энкодерами, но знаете о свёрточных нейронных сетях (Convolutional Neural Networks — CNNs), то, по сути, вы уже знаете, что делает автоэнкодер.
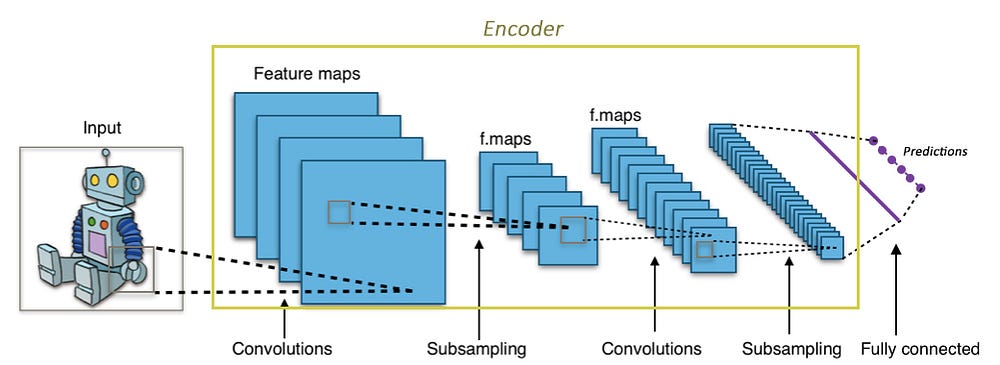
Свёрточные слои принимают большое изображение (к примеру, тензор 3-го ранга размером 299х299х3) и преобразует его в более компактный, плотный вид (к примеру, тензор 1-го ранга размером 1000). Этот сжатый вид затем использует нейросеть для классификации изображения.
Энкодер выполняет похожие операции. Это нейросеть, которая принимает входные данные и выдаёт их в сжатом виде (т.е. выполняет их кодирование), которые содержит достаточно информации для трансформации этих данным следующей нейросетью в желаемый формат. Обычно энкодер обучается одновременно с другими частями нейросети на основе метода обратного распространения, что позволяет ему производить вид кодирования, необходимый в конкретной задаче. В CNN кодирование изображения в массив из 1000 элементов производится таким образом, что этот массив становится пригодным для задач классификации.
Автоэнкодеры используют ту же идею, но в другом виде: энкодер генерирует закодированные данные, пригодные для восстановления входных данных.
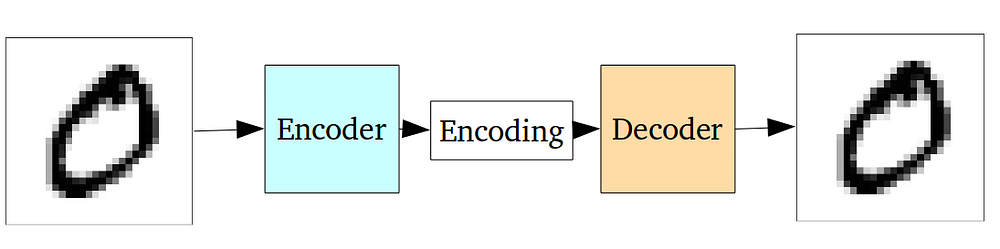
Нейросеть обычно обучается как единое целое. Функция потерь выбирается как среднеквадратичная ошибка или как кросс-энтропия между входными и выходными данными, также известная как потеря восстановления (reconstruction loss), которая не позволяет нейросети создавать выходные данные, сильно отличающиеся от входных.
Так как зашифрованные данные (которые являются просто выходными данными скрытого слоя в середине) имеют намного меньший размер, чем входные, то получается, что энкодер теряет часть информации. В то же время, энкодер обучается сохранять как можно больше значимой информации и откидывать второстепенные детали. В свою очередь, декодер обучается принимать зашифрованные данные и правильным образом восстанавливать из них входные изображения. Две этих нейросети вместе формируют автоэнкодер.
Проблема классических автоэнкодеров
Классические автоэнкодеры обучаются кодировать входные данные и восстанавливать их. Однако область их применения ограничивается в основном созданием шумоподавляющих кодеров.
Фундаментальная проблема автоэнкодеров заключается в том, что скрытое пространство, в котором они кодируют данные, и в котором лежат их закодированные векторы, может не быть непрерывным и не позволять производить интерполяцию.
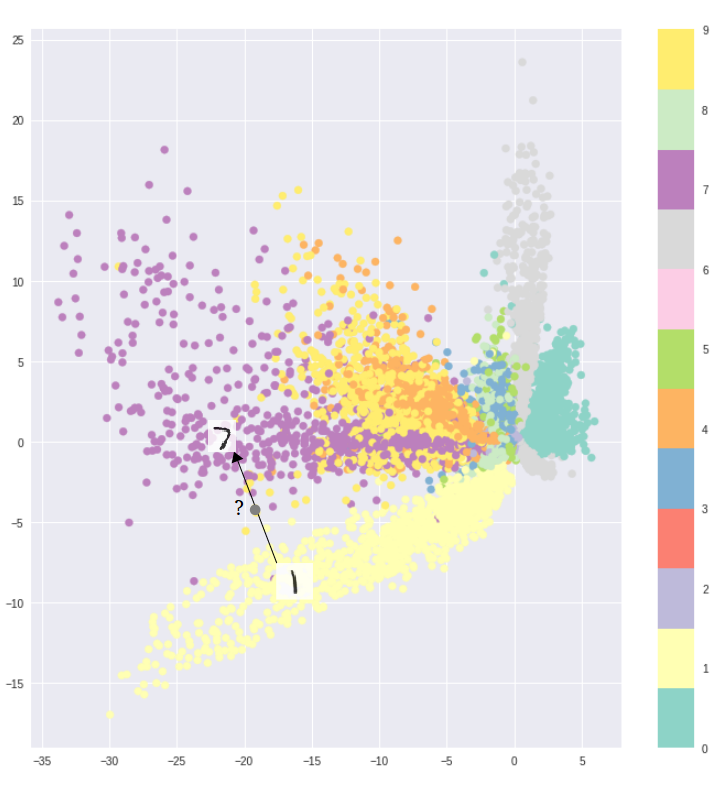
К примеру, обучение автоэнкодера на датасете MNIST и визуализация закодированных данных из двумерного скрытого пространства наглядно показывают формирование отдельных кластеров. Это имеет смысл, так как отдельные векторы кодирования для каждого типа изображения облегчают расшифровку данных, производимую энкодером.
Всё замечательно, если вам необходимо просто воспроизвести исходные изображения. Однако, если вы строите генеративную модель, ваша цель не простое дублирование изображений. В этом случае вы хотите получить случайное или видоизмененное изображение, восстановленное из непрерывного скрытого пространства.
Если пространство имеет разрывы (например, промежутки между кластерами), и вы пытаетесь сгенерировать изображение на основе закодированных данных из этого промежутка, то декодер выдаст нереалистичное изображение, потому что не имеет представления о том, что делать с этой областью скрытого пространства.
Вариационные Автоэнкодеры
Вариационный автоэнкодер (VAE) имеет одно уникальное свойство, которое отличает его от стандартного автоэнкодера. Именно это свойство делает вариационные автоэнкодеры столь полезными при генерации данных: их скрытое пространство по построению является непрерывным, позволяя выполнять случайные преобразования и интерполяцию.
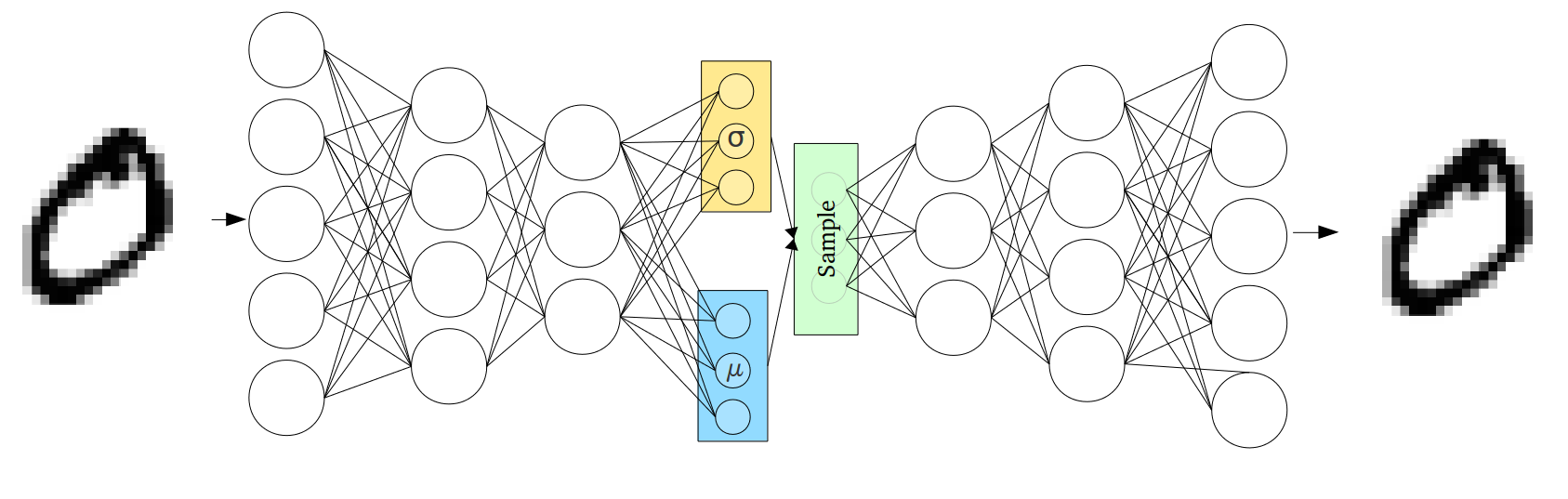
Непрерывность скрытого пространства достигается неожиданным способом: энкодер выдаёт не один вектор размера n, а два вектора размера n – вектор средних значений µ и вектор стандартных отклонений σ.
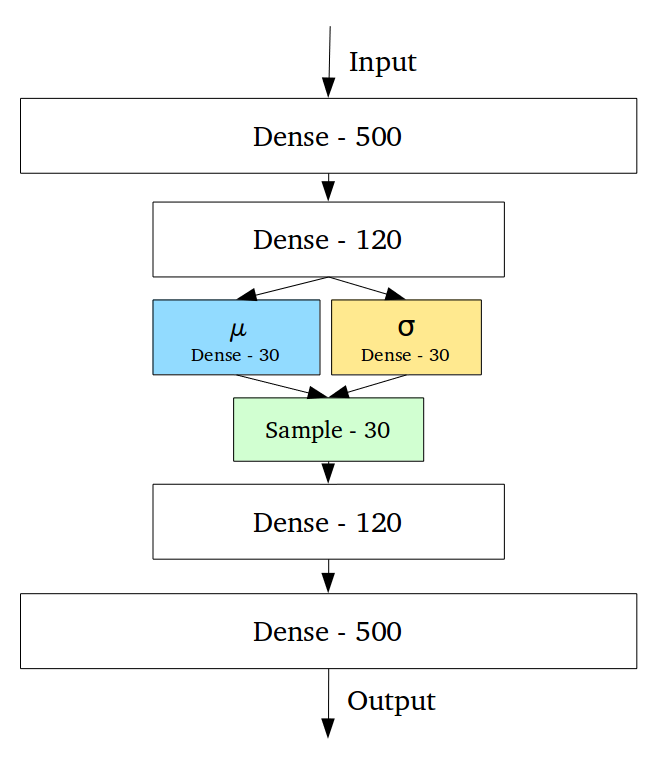
Вариационные автоэнкодеры формируют параметры вектора длины n из случайных величин Xi, причем i-е элементы векторов µ и σ являются средним и стандартным отклонением i-й случайной величины Xi. Вместе эти величины образуют n-мерный случайный вектор, который посылается на декодер для восстановления данных:

Эта так называемая стохастическая генерация означает, что даже для одинаковых входных данных результат кодирования будет разным вследствие случайности выбора вектора кодирования:
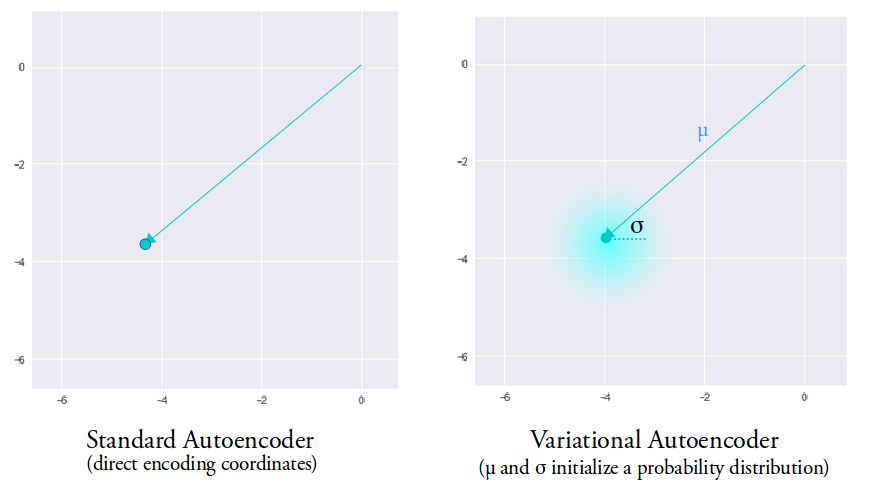
Среднее значение вектора определяет точку, вблизи которой будет вершина вектора, в то время как стандартное отклонение определяет насколько далеко может отстоять вершина от этого среднего. Таким образом, вершина вектора кодирования может лежать внутри n-мерного круга (см. рис. выше). Поэтому входному объекту соответствует уже не одна точка в скрытом пространстве, а некоторая непрерывная область. Этот факт позволяет декодеру работать не с одним единственным вектором кодирования, соответствующим входным данным, а с их набором, благодаря чему в восстановление даже одного изображения вносится доля вариативности. Код реализации такого подхода.
Теперь модель обладает вариативностью даже в пределах одного вектора кодирования, так как скрытое пространство локально непрерывно, т.е. непрерывно для каждого образца входных данных. В идеальном случае, нам хотелось бы перекрытия этих локальных областей и для образцов входных данных, которые не сильно похожи друг на друга, чтобы производить интерполяцию между ними. Однако, так как нет ограничений на значения, принимаемые векторами µ и σ, энкодер может быть обучен генерировать сильно отличающиеся µ для разных образцов входных данных, тем самым сильно удаляя их представления друг от друга в скрытом пространстве. Кроме того, энкодер будет минимизировать σ для того, чтобы векторы кодирования не сильно отличались для одного образца. Таким образом, декодер получает данные с малой степенью неопределенности, что позволяет ему эффективно восстанавливать данные из тренировочных сетов, но при этом мы можем не иметь непрерывного пространства:
Мы хотим, чтобы все области в скрытом пространстве были как можно ближе друг к другу, но при этом оставались различимыми как отдельные составляющие. В этом случае мы можем производить гладкую интерполяцию и создавать новые данные на выходе.
Для того чтобы достичь этого, в функцию потерь вводится так называемая Kullback–Leibler расходимость (KL divergence). КL расходимость между двумя функциями распределения показывает насколько сильно они отличаются друг от друга. Минимизация KL расходимости означает оптимизацию параметров распределения µ и σ таким образом, что они становятся близки к параметрам целевого распределения.
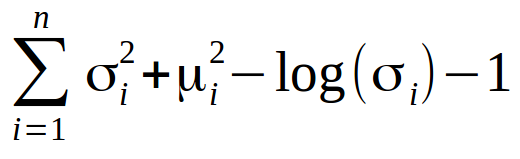
Для Вариационных Автоэнкодеров KL потери эквивалентны сумме всех KL расходимостей между распределением компонент Xi~N(μi, σi²) в векторе Х и нормальным распределением. Минимум достигается, когда µi = 0 и σi = 1.
Как видно, учёт KL потерь заставляет энкодер помещать каждую отдельную область кодирования в окрестности некоторой точки в скрытом пространстве.
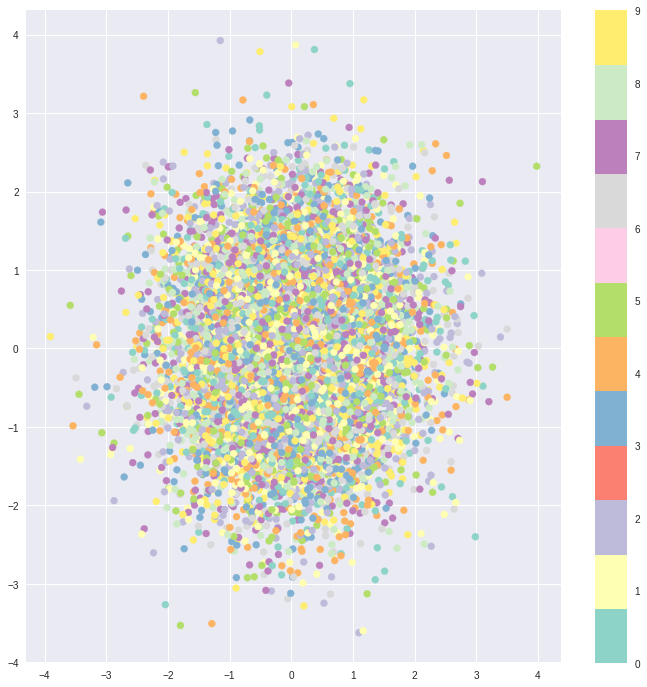
При использовании KL потерь области кодирования расположены случайным образом в окрестности выделенной точки в скрытом пространстве со слабым учётом сходства между образцами входных данных. Поэтому декодер не способен извлечь что-либо значащее из этого пространства:
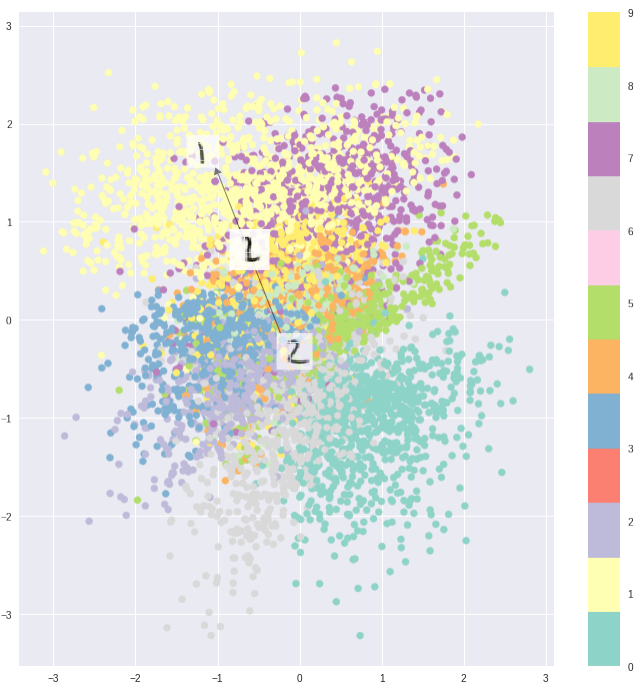
Однако, оптимизируя и энкодер и декодер, мы получаем скрытое пространство, которое отражает схожесть соседних векторов на глобальном уровне, и имеет вид плотно расположенных областей возле начала координат скрытого пространства:
Достигнутый результат – это компромисс между кластерной природой потерь восстановления, необходимой декодеру, и нашим желанием иметь плотно расположенные векторы при использовании KL потерь. И это здорово, потому что теперь, если вы хотите восстановить входные данные, вы просто выбираете подходящее распределение и посылаете его в декодер. А если вам необходимо произвести интерполяцию, то вы можете смело её осуществить, так как пространство представляет собой гладкое распределение особенностей, что декодер без труда способен обработать.
Векторная алгебра
Как мы производим гладкую интерполяцию, о которой было так много сказано выше? Ответ кроется в простой векторной алгебре — рассмотрим её.
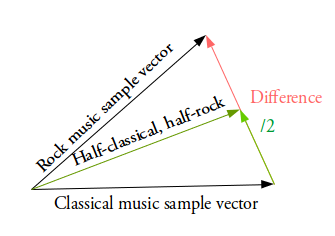
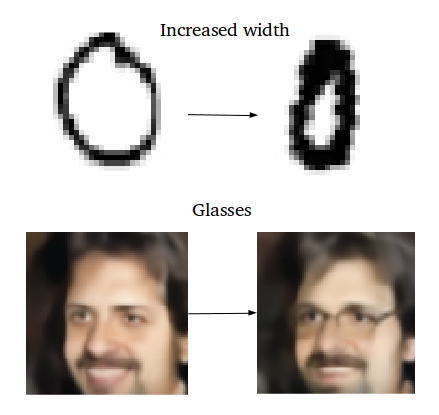
К примеру, вы хотите сгенерировать новый образец как нечто среднее между двумя заданными образцами. В этом случае вы находите разницу между двумя средними векторами этих образцов, делите её пополам и прибавляете этот результат к вектору, который был вычитаемым. Вы получили вектор, который является чем-то средним между двумя заданными векторами. Расшифровывая его, вы получите желаемый результат (см. рис.выше).
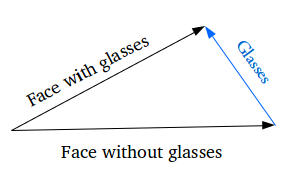
Как насчёт генерации специфических особенностей: например, добавления очков на портрет? Мы находим два схожих образца – один с очками, другой – без них, получаем их вектора с помощью энкодера и находим их разницу. Затем прибавляем этот разностный вектор, который и отвечает за наличие очков, к вектору портрета без очков и расшифровываем получившийся вектор с помощью декодера.
Улучшения VAE
Существует множество улучшений вариационных автоэнкодеров. К примеру, вы можете заменить стандартную пару из полностью соединённых энкодера и декодера на пару CNN-DNN энкодера и декодера, прямо как в этом проекте, в рамках которого были созданы искусственные фото людей.

Кроме того, вы можете обучать автоэнкодер, используя LSTM пару энкодер-декодер и модифицированную версию архитектуры seq2seq,и использовать его для дискретных данных. К примеру, генерировать текст или даже производить интерполяцию между MIDI сигнашами, как делает Google Brain’s Magenta’s MusicVAE:
Вариационные Автоэнкодеры способны работать с удивительно разнообразными типами данных: последовательными или непоследовательными, непрерывными или дискретными и т.д. Эта характерная черта делает их наиболее эффективными инструментами генерации и обуславливает их высокую популярность в сфере машинного обучения.
Интересные статьи:
- Генеративно-состязательная нейросеть (GAN). Руководство для новичков
- Деформирующие автоэнкодеры
- LSTM — нейронная сеть с долгой краткосрочной памятью
Генерируйте видео, изображения и аватары с помощью сервиса FabulaAI. Получите 10 бесплатных генераций сразу после регистрации!